Efficient compilation of expressive problem space specifications to neural network solvers

Recent work has described the presence of the embedding gap in neural network verification. On one side of the gap is a high-level specification about the network's behaviour, written by a domain expert in terms of the interpretable problem space. On the other side are a logically-equivalent set of satisfiability queries, expressed in the uninterpretable embedding space in a form suitable for neural network solvers. In this paper we describe an algorithm for compiling the former to the latter. We explore and overcome complications that arise from targeting neural network solvers as opposed to standard SMT solvers.

Vehicle: Bridging the Embedding Gap in the Verification of Neuro-Symbolic Programs

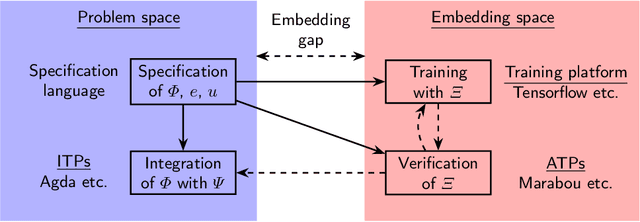
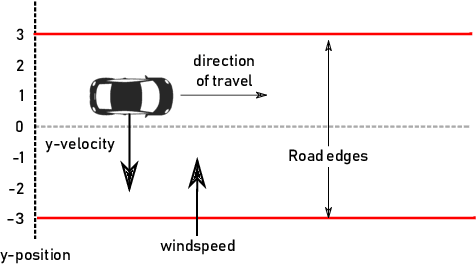
Neuro-symbolic programs -- programs containing both machine learning components and traditional symbolic code -- are becoming increasingly widespread. However, we believe that there is still a lack of a general methodology for verifying these programs whose correctness depends on the behaviour of the machine learning components. In this paper, we identify the ``embedding gap'' -- the lack of techniques for linking semantically-meaningful ``problem-space'' properties to equivalent ``embedding-space'' properties -- as one of the key issues, and describe Vehicle, a tool designed to facilitate the end-to-end verification of neural-symbolic programs in a modular fashion. Vehicle provides a convenient language for specifying ``problem-space'' properties of neural networks and declaring their relationship to the ``embedding-space", and a powerful compiler that automates interpretation of these properties in the language of a chosen machine-learning training environment, neural network verifier, and interactive theorem prover. We demonstrate Vehicle's utility by using it to formally verify the safety of a simple autonomous car equipped with a neural network controller.

Vehicle: Interfacing Neural Network Verifiers with Interactive Theorem Provers

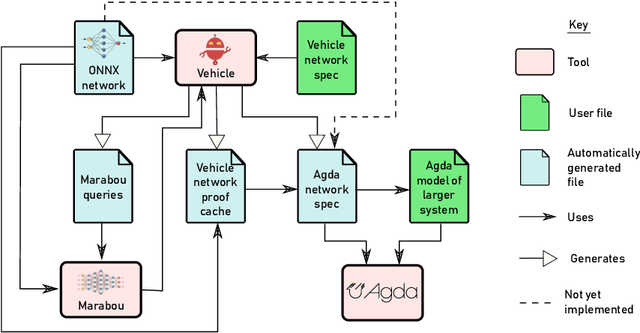
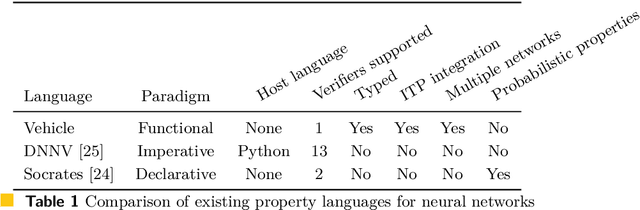
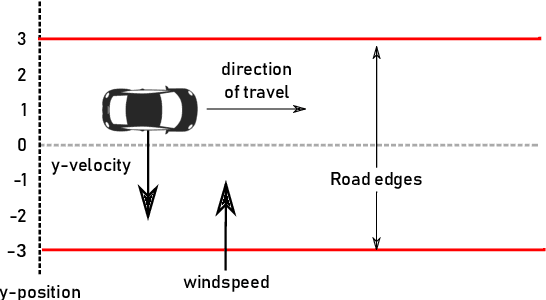
Verification of neural networks is currently a hot topic in automated theorem proving. Progress has been rapid and there are now a wide range of tools available that can verify properties of networks with hundreds of thousands of nodes. In theory this opens the door to the verification of larger control systems that make use of neural network components. However, although work has managed to incorporate the results of these verifiers to prove larger properties of individual systems, there is currently no general methodology for bridging the gap between verifiers and interactive theorem provers (ITPs). In this paper we present Vehicle, our solution to this problem. Vehicle is equipped with an expressive domain specific language for stating neural network specifications which can be compiled to both verifiers and ITPs. It overcomes previous issues with maintainability and scalability in similar ITP formalisations by using a standard ONNX file as the single canonical representation of the network. We demonstrate its utility by using it to connect the neural network verifier Marabou to Agda and then formally verifying that a car steered by a neural network never leaves the road, even in the face of an unpredictable cross wind and imperfect sensors. The network has over 20,000 nodes, and therefore this proof represents an improvement of 3 orders of magnitude over prior proofs about neural network enhanced systems in ITPs.