NLP Verification: Towards a General Methodology for Certifying Robustness

Deep neural networks have exhibited substantial success in the field of Natural Language Processing (NLP) and ensuring their safety and reliability is crucial: there are safety critical contexts where such models must be robust to variability or attack, and give guarantees over their output. Unlike Computer Vision, NLP lacks a unified verification methodology and, despite recent advancements in literature, they are often light on the pragmatical issues of NLP verification. In this paper, we make an attempt to distil and evaluate general components of an NLP verification pipeline, that emerges from the progress in the field to date. Our contributions are two-fold. Firstly, we give a general characterisation of verifiable subspaces that result from embedding sentences into continuous spaces. We identify, and give an effective method to deal with, the technical challenge of semantic generalisability of verified subspaces; and propose it as a standard metric in the NLP verification pipelines (alongside with the standard metrics of model accuracy and model verifiability). Secondly, we propose a general methodology to analyse the effect of the embedding gap, a problem that refers to the discrepancy between verification of geometric subpspaces on the one hand, and semantic meaning of sentences which the geometric subspaces are supposed to represent, on the other hand. In extreme cases, poor choices in embedding of sentences may invalidate verification results. We propose a number of practical NLP methods that can help to identify the effects of the embedding gap; and in particular we propose the metric of falsifiability of semantic subpspaces as another fundamental metric to be reported as part of the NLP verification pipeline. We believe that together these general principles pave the way towards a more consolidated and effective development of this new domain.

Efficient compilation of expressive problem space specifications to neural network solvers

Recent work has described the presence of the embedding gap in neural network verification. On one side of the gap is a high-level specification about the network's behaviour, written by a domain expert in terms of the interpretable problem space. On the other side are a logically-equivalent set of satisfiability queries, expressed in the uninterpretable embedding space in a form suitable for neural network solvers. In this paper we describe an algorithm for compiling the former to the latter. We explore and overcome complications that arise from targeting neural network solvers as opposed to standard SMT solvers.

Vehicle: Bridging the Embedding Gap in the Verification of Neuro-Symbolic Programs

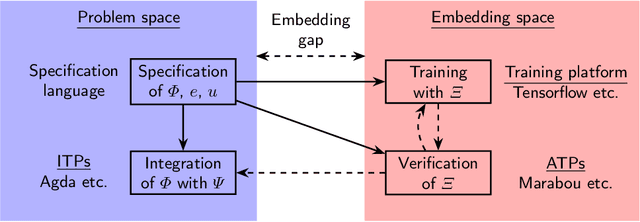
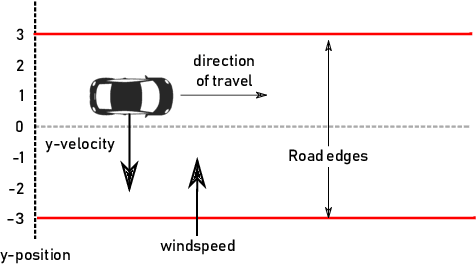
Neuro-symbolic programs -- programs containing both machine learning components and traditional symbolic code -- are becoming increasingly widespread. However, we believe that there is still a lack of a general methodology for verifying these programs whose correctness depends on the behaviour of the machine learning components. In this paper, we identify the ``embedding gap'' -- the lack of techniques for linking semantically-meaningful ``problem-space'' properties to equivalent ``embedding-space'' properties -- as one of the key issues, and describe Vehicle, a tool designed to facilitate the end-to-end verification of neural-symbolic programs in a modular fashion. Vehicle provides a convenient language for specifying ``problem-space'' properties of neural networks and declaring their relationship to the ``embedding-space", and a powerful compiler that automates interpretation of these properties in the language of a chosen machine-learning training environment, neural network verifier, and interactive theorem prover. We demonstrate Vehicle's utility by using it to formally verify the safety of a simple autonomous car equipped with a neural network controller.

ANTONIO: Towards a Systematic Method of Generating NLP Benchmarks for Verification

Verification of machine learning models used in Natural Language Processing (NLP) is known to be a hard problem. In particular, many known neural network verification methods that work for computer vision and other numeric datasets do not work for NLP. Here, we study technical reasons that underlie this problem. Based on this analysis, we propose practical methods and heuristics for preparing NLP datasets and models in a way that renders them amenable to known verification methods based on abstract interpretation. We implement these methods as a Python library called ANTONIO that links to the neural network verifiers ERAN and Marabou. We perform evaluation of the tool using an NLP dataset R-U-A-Robot suggested as a benchmark for verifying legally critical NLP applications. We hope that, thanks to its general applicability, this work will open novel possibilities for including NLP verification problems into neural network verification competitions, and will popularise NLP problems within this community.

Logic of Differentiable Logics: Towards a Uniform Semantics of DL

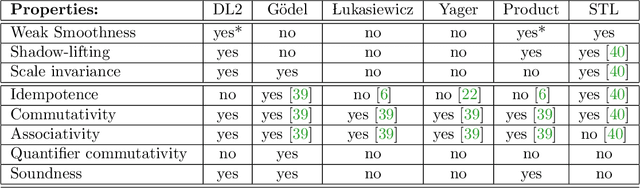
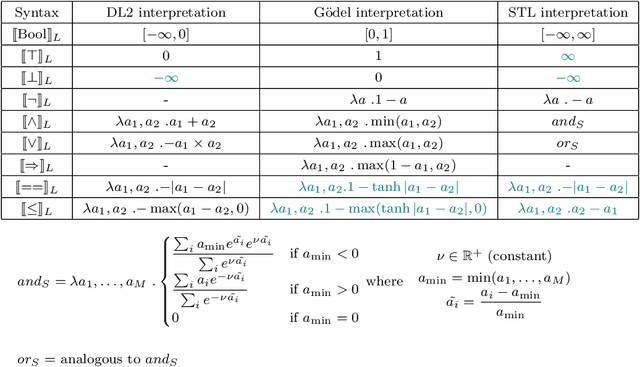
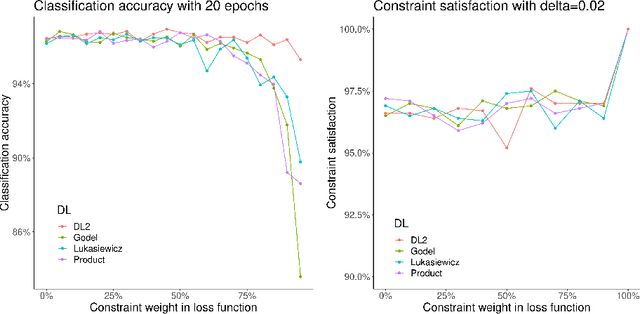
Differentiable logics (DL) have recently been proposed as a method of training neural networks to satisfy logical specifications. A DL consists of a syntax in which specifications are stated and an interpretation function that translates expressions in the syntax into loss functions. These loss functions can then be used during training with standard gradient descent algorithms. The variety of existing DLs and the differing levels of formality with which they are treated makes a systematic comparative study of their properties and implementations difficult. This paper remedies this problem by suggesting a meta-language for defining DLs that we call the Logic of Differentiable Logics, or LDL. Syntactically, it generalises the syntax of existing DLs to FOL, and for the first time introduces the formalism for reasoning about vectors and learners. Semantically, it introduces a general interpretation function that can be instantiated to define loss functions arising from different existing DLs. We use LDL to establish several theoretical properties of existing DLs, and to conduct their empirical study in neural network verification.

Differentiable Logics for Neural Network Training and Verification

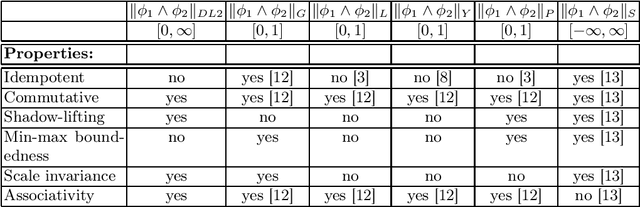
The rising popularity of neural networks (NNs) in recent years and their increasing prevalence in real-world applications have drawn attention to the importance of their verification. While verification is known to be computationally difficult theoretically, many techniques have been proposed for solving it in practice. It has been observed in the literature that by default neural networks rarely satisfy logical constraints that we want to verify. A good course of action is to train the given NN to satisfy said constraint prior to verifying them. This idea is sometimes referred to as continuous verification, referring to the loop between training and verification. Usually training with constraints is implemented by specifying a translation for a given formal logic language into loss functions. These loss functions are then used to train neural networks. Because for training purposes these functions need to be differentiable, these translations are called differentiable logics (DL). This raises several research questions. What kind of differentiable logics are possible? What difference does a specific choice of DL make in the context of continuous verification? What are the desirable criteria for a DL viewed from the point of view of the resulting loss function? In this extended abstract we will discuss and answer these questions.

Why Robust Natural Language Understanding is a Challenge

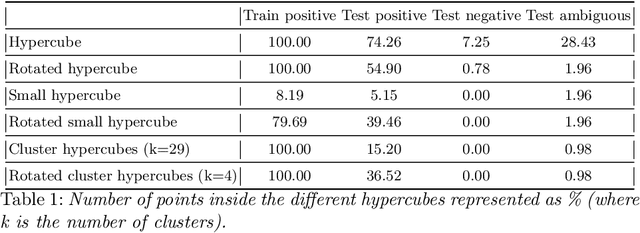
With the proliferation of Deep Machine Learning into real-life applications, a particular property of this technology has been brought to attention: Neural Networks notoriously present low robustness and can be highly sensitive to small input perturbations. Recently, many methods for verifying networks' general properties of robustness have been proposed, but they are mostly applied in Computer Vision. In this paper we propose a Verification method for Natural Language Understanding classification based on larger regions of interest, and we discuss the challenges of such task. We observe that, although the data is almost linearly separable, the verifier does not output positive results and we explain the problems and implications.

Vehicle: Interfacing Neural Network Verifiers with Interactive Theorem Provers

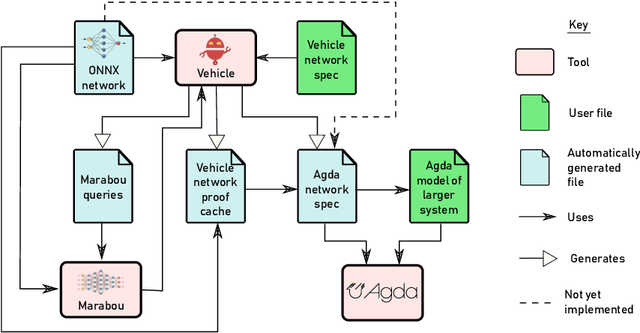
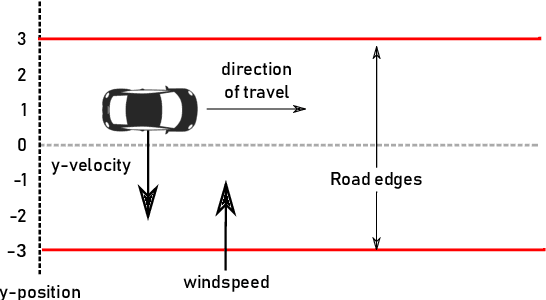
Verification of neural networks is currently a hot topic in automated theorem proving. Progress has been rapid and there are now a wide range of tools available that can verify properties of networks with hundreds of thousands of nodes. In theory this opens the door to the verification of larger control systems that make use of neural network components. However, although work has managed to incorporate the results of these verifiers to prove larger properties of individual systems, there is currently no general methodology for bridging the gap between verifiers and interactive theorem provers (ITPs). In this paper we present Vehicle, our solution to this problem. Vehicle is equipped with an expressive domain specific language for stating neural network specifications which can be compiled to both verifiers and ITPs. It overcomes previous issues with maintainability and scalability in similar ITP formalisations by using a standard ONNX file as the single canonical representation of the network. We demonstrate its utility by using it to connect the neural network verifier Marabou to Agda and then formally verifying that a car steered by a neural network never leaves the road, even in the face of an unpredictable cross wind and imperfect sensors. The network has over 20,000 nodes, and therefore this proof represents an improvement of 3 orders of magnitude over prior proofs about neural network enhanced systems in ITPs.

Actions You Can Handle: Dependent Types for AI Plans

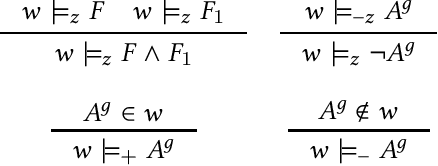
Verification of AI is a challenge that has engineering, algorithmic and programming language components. For example, AI planners are deployed to model actions of autonomous agents. They comprise a number of searching algorithms that, given a set of specified properties, find a sequence of actions that satisfy these properties. Although AI planners are mature tools from the algorithmic and engineering points of view, they have limitations as programming languages. Decidable and efficient automated search entails restrictions on the syntax of the language, prohibiting use of higher-order properties or recursion. This paper proposes a methodology for embedding plans produced by AI planners into dependently-typed language Agda, which enables users to reason about and verify more general and abstract properties of plans, and also provides a more holistic programming language infrastructure for modelling plan execution.