Actions You Can Handle: Dependent Types for AI Plans

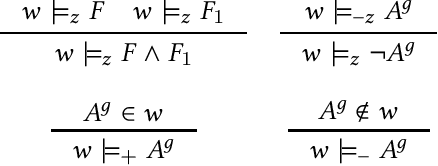
Verification of AI is a challenge that has engineering, algorithmic and programming language components. For example, AI planners are deployed to model actions of autonomous agents. They comprise a number of searching algorithms that, given a set of specified properties, find a sequence of actions that satisfy these properties. Although AI planners are mature tools from the algorithmic and engineering points of view, they have limitations as programming languages. Decidable and efficient automated search entails restrictions on the syntax of the language, prohibiting use of higher-order properties or recursion. This paper proposes a methodology for embedding plans produced by AI planners into dependently-typed language Agda, which enables users to reason about and verify more general and abstract properties of plans, and also provides a more holistic programming language infrastructure for modelling plan execution.

Proof-Carrying Plans: a Resource Logic for AI Planning

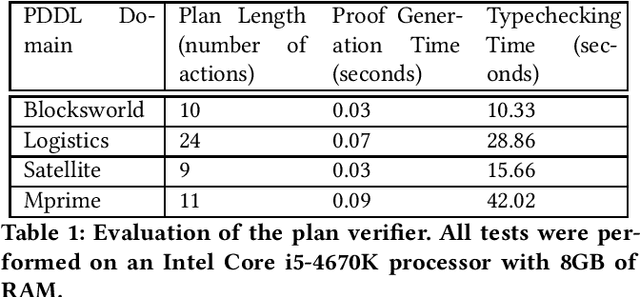
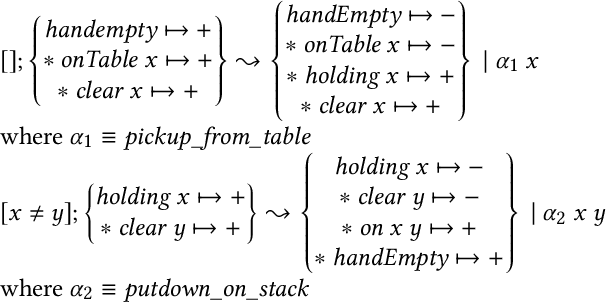
Recent trends in AI verification and Explainable AI have raised the question of whether AI planning techniques can be verified. In this paper, we present a novel resource logic, the Proof Carrying Plans (PCP) logic that can be used to verify plans produced by AI planners. The PCP logic takes inspiration from existing resource logics (such as Linear logic and Separation logic) as well as Hoare logic when it comes to modelling states and resource-aware plan execution. It also capitalises on the Curry-Howard approach to logics, in its treatment of plans as functions and plan pre- and post-conditions as types. This paper presents two main results. From the theoretical perspective, we show that the PCP logic is sound relative to the standard possible world semantics used in AI planning. From the practical perspective, we present a complete Agda formalisation of the PCP logic and of its soundness proof. Moreover, we showcase the Curry-Howard, or functional, value of this implementation by supplementing it with the library that parses AI plans into Agda's proofs automatically. We provide evaluation of this library and the resulting Agda functions.