A Neurosymbolic Framework for Bias Correction in CNNs

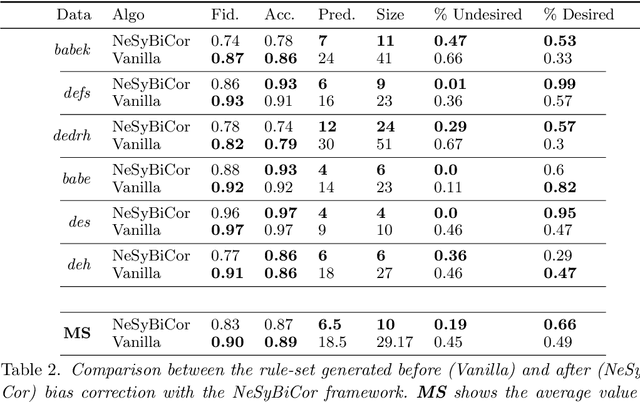
Recent efforts in interpreting Convolutional Neural Networks (CNNs) focus on translating the activation of CNN filters into stratified Answer Set Programming (ASP) rule-sets. The CNN filters are known to capture high-level image concepts, thus the predicates in the rule-set are mapped to the concept that their corresponding filter represents. Hence, the rule-set effectively exemplifies the decision-making process of the CNN in terms of the concepts that it learns for any image classification task. These rule-sets help expose and understand the biases in CNNs, although correcting the biases effectively remains a challenge. We introduce a neurosymbolic framework called NeSyBiCor for bias correction in a trained CNN. Given symbolic concepts that the CNN is biased towards, expressed as ASP constraints, we convert the undesirable and desirable concepts to their corresponding vector representations. Then, the CNN is retrained using our novel semantic similarity loss that pushes the filters away from the representations of concepts that are undesirable while pushing them closer to the concepts that are desirable. The final ASP rule-set obtained after retraining, satisfies the constraints to a high degree, thus showing the revision in the knowledge of the CNN for the image classification task. We demonstrate that our NeSyBiCor framework successfully corrects the biases of CNNs trained with subsets of classes from the Places dataset while sacrificing minimal accuracy and improving interpretability, by greatly decreasing the size of the final bias-corrected rule-set w.r.t. the initial rule-set.

Logic of Differentiable Logics: Towards a Uniform Semantics of DL

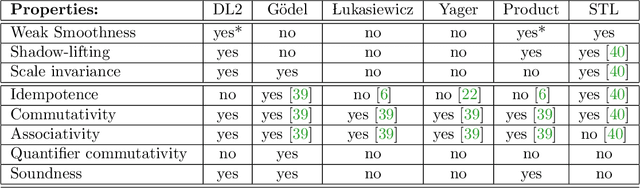
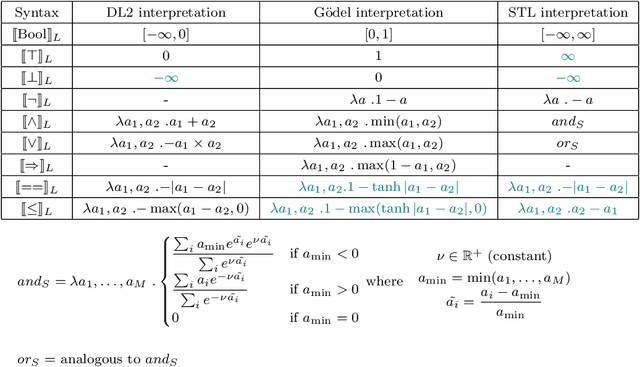
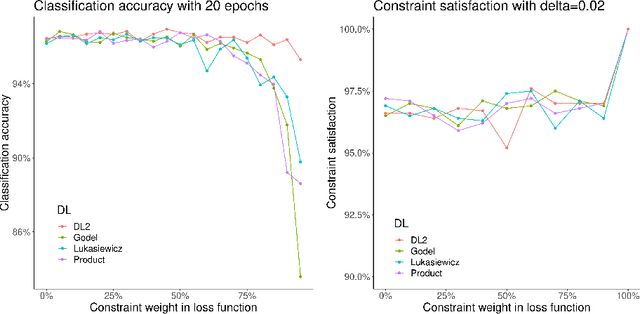
Differentiable logics (DL) have recently been proposed as a method of training neural networks to satisfy logical specifications. A DL consists of a syntax in which specifications are stated and an interpretation function that translates expressions in the syntax into loss functions. These loss functions can then be used during training with standard gradient descent algorithms. The variety of existing DLs and the differing levels of formality with which they are treated makes a systematic comparative study of their properties and implementations difficult. This paper remedies this problem by suggesting a meta-language for defining DLs that we call the Logic of Differentiable Logics, or LDL. Syntactically, it generalises the syntax of existing DLs to FOL, and for the first time introduces the formalism for reasoning about vectors and learners. Semantically, it introduces a general interpretation function that can be instantiated to define loss functions arising from different existing DLs. We use LDL to establish several theoretical properties of existing DLs, and to conduct their empirical study in neural network verification.