A Certified Proof Checker for Deep Neural Network Verification

Recent advances in the verification of deep neural networks (DNNs) have opened the way for broader usage of DNN verification technology in many application areas, including safety-critical ones. DNN verifiers are themselves complex programs that have been shown to be susceptible to errors and imprecisions; this in turn has raised the question of trust in DNN verifiers. One prominent attempt to address this issue is enhancing DNN verifiers with the capability of producing proofs of their results that are subject to independent algorithmic certification (proof checking). Formulations of proof production and proof checking already exist on top of the state-of-the-art Marabou DNN verifier. The native implementation of the proof checking algorithm for Marabou was done in C++ and itself raised the question of trust in the code (e.g., in the precision of floating point calculations or guarantees for implementation soundness). Here, we present an alternative implementation of the Marabou proof checking algorithm in Imandra -- an industrial functional programming language and prover -- that allows us to obtain an implementation with formal guarantees, including proofs of mathematical results underlying the algorithm, such as the use of the Farkas lemma.

Towards a Certified Proof Checker for Deep Neural Network Verification

Recent developments in deep neural networks (DNNs) have led to their adoption in safety-critical systems, which in turn has heightened the need for guaranteeing their safety. These safety properties of DNNs can be proven using tools developed by the verification community. However, these tools are themselves prone to implementation bugs and numerical stability problems, which make their reliability questionable. To overcome this, some verifiers produce proofs of their results which can be checked by a trusted checker. In this work, we present a novel implementation of a proof checker for DNN verification. It improves on existing implementations by offering numerical stability and greater verifiability. To achieve this, we leverage two key capabilities of Imandra, an industrial theorem prover: its support of infinite precision real arithmetic and its formal verification infrastructure. So far, we have implemented a proof checker in Imandra, specified its correctness properties and started to verify the checker's compliance with them. Our ongoing work focuses on completing the formal verification of the checker and further optimizing its performance.

Logic of Differentiable Logics: Towards a Uniform Semantics of DL

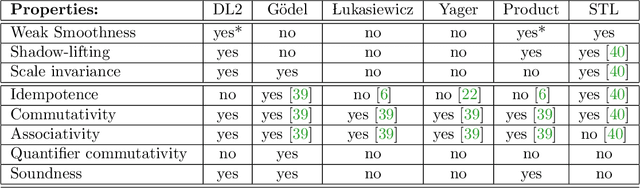
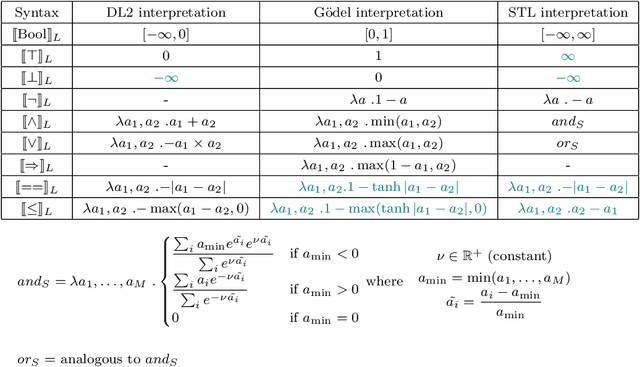
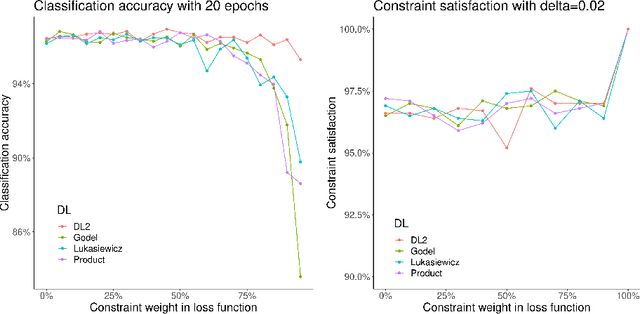
Differentiable logics (DL) have recently been proposed as a method of training neural networks to satisfy logical specifications. A DL consists of a syntax in which specifications are stated and an interpretation function that translates expressions in the syntax into loss functions. These loss functions can then be used during training with standard gradient descent algorithms. The variety of existing DLs and the differing levels of formality with which they are treated makes a systematic comparative study of their properties and implementations difficult. This paper remedies this problem by suggesting a meta-language for defining DLs that we call the Logic of Differentiable Logics, or LDL. Syntactically, it generalises the syntax of existing DLs to FOL, and for the first time introduces the formalism for reasoning about vectors and learners. Semantically, it introduces a general interpretation function that can be instantiated to define loss functions arising from different existing DLs. We use LDL to establish several theoretical properties of existing DLs, and to conduct their empirical study in neural network verification.