A Certified Proof Checker for Deep Neural Network Verification

Recent advances in the verification of deep neural networks (DNNs) have opened the way for broader usage of DNN verification technology in many application areas, including safety-critical ones. DNN verifiers are themselves complex programs that have been shown to be susceptible to errors and imprecisions; this in turn has raised the question of trust in DNN verifiers. One prominent attempt to address this issue is enhancing DNN verifiers with the capability of producing proofs of their results that are subject to independent algorithmic certification (proof checking). Formulations of proof production and proof checking already exist on top of the state-of-the-art Marabou DNN verifier. The native implementation of the proof checking algorithm for Marabou was done in C++ and itself raised the question of trust in the code (e.g., in the precision of floating point calculations or guarantees for implementation soundness). Here, we present an alternative implementation of the Marabou proof checking algorithm in Imandra -- an industrial functional programming language and prover -- that allows us to obtain an implementation with formal guarantees, including proofs of mathematical results underlying the algorithm, such as the use of the Farkas lemma.

NLP Verification: Towards a General Methodology for Certifying Robustness

Deep neural networks have exhibited substantial success in the field of Natural Language Processing (NLP) and ensuring their safety and reliability is crucial: there are safety critical contexts where such models must be robust to variability or attack, and give guarantees over their output. Unlike Computer Vision, NLP lacks a unified verification methodology and, despite recent advancements in literature, they are often light on the pragmatical issues of NLP verification. In this paper, we make an attempt to distil and evaluate general components of an NLP verification pipeline, that emerges from the progress in the field to date. Our contributions are two-fold. Firstly, we give a general characterisation of verifiable subspaces that result from embedding sentences into continuous spaces. We identify, and give an effective method to deal with, the technical challenge of semantic generalisability of verified subspaces; and propose it as a standard metric in the NLP verification pipelines (alongside with the standard metrics of model accuracy and model verifiability). Secondly, we propose a general methodology to analyse the effect of the embedding gap, a problem that refers to the discrepancy between verification of geometric subpspaces on the one hand, and semantic meaning of sentences which the geometric subspaces are supposed to represent, on the other hand. In extreme cases, poor choices in embedding of sentences may invalidate verification results. We propose a number of practical NLP methods that can help to identify the effects of the embedding gap; and in particular we propose the metric of falsifiability of semantic subpspaces as another fundamental metric to be reported as part of the NLP verification pipeline. We believe that together these general principles pave the way towards a more consolidated and effective development of this new domain.

Marabou 2.0: A Versatile Formal Analyzer of Neural Networks

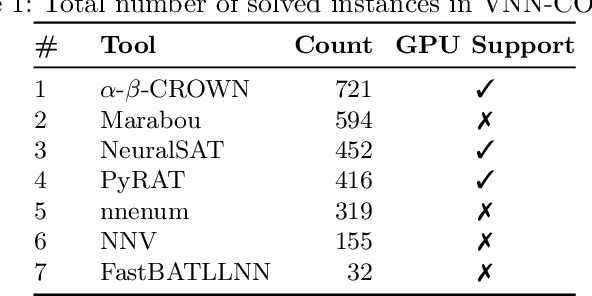
This paper serves as a comprehensive system description of version 2.0 of the Marabou framework for formal analysis of neural networks. We discuss the tool's architectural design and highlight the major features and components introduced since its initial release.

Robustness Assessment of a Runway Object Classifier for Safe Aircraft Taxiing

As deep neural networks (DNNs) are becoming the prominent solution for many computational problems, the aviation industry seeks to explore their potential in alleviating pilot workload and in improving operational safety. However, the use of DNNs in this type of safety-critical applications requires a thorough certification process. This need can be addressed through formal verification, which provides rigorous assurances -- e.g.,~by proving the absence of certain mispredictions. In this case-study paper, we demonstrate this process using an image-classifier DNN currently under development at Airbus and intended for use during the aircraft taxiing phase. We use formal methods to assess this DNN's robustness to three common image perturbation types: noise, brightness and contrast, and some of their combinations. This process entails multiple invocations of the underlying verifier, which might be computationally expensive; and we therefore propose a method that leverages the monotonicity of these robustness properties, as well as the results of past verification queries, in order to reduce the overall number of verification queries required by nearly 60%. Our results provide an indication of the level of robustness achieved by the DNN classifier under study, and indicate that it is considerably more vulnerable to noise than to brightness or contrast perturbations.

Towards a Certified Proof Checker for Deep Neural Network Verification

Recent developments in deep neural networks (DNNs) have led to their adoption in safety-critical systems, which in turn has heightened the need for guaranteeing their safety. These safety properties of DNNs can be proven using tools developed by the verification community. However, these tools are themselves prone to implementation bugs and numerical stability problems, which make their reliability questionable. To overcome this, some verifiers produce proofs of their results which can be checked by a trusted checker. In this work, we present a novel implementation of a proof checker for DNN verification. It improves on existing implementations by offering numerical stability and greater verifiability. To achieve this, we leverage two key capabilities of Imandra, an industrial theorem prover: its support of infinite precision real arithmetic and its formal verification infrastructure. So far, we have implemented a proof checker in Imandra, specified its correctness properties and started to verify the checker's compliance with them. Our ongoing work focuses on completing the formal verification of the checker and further optimizing its performance.

ANTONIO: Towards a Systematic Method of Generating NLP Benchmarks for Verification

Verification of machine learning models used in Natural Language Processing (NLP) is known to be a hard problem. In particular, many known neural network verification methods that work for computer vision and other numeric datasets do not work for NLP. Here, we study technical reasons that underlie this problem. Based on this analysis, we propose practical methods and heuristics for preparing NLP datasets and models in a way that renders them amenable to known verification methods based on abstract interpretation. We implement these methods as a Python library called ANTONIO that links to the neural network verifiers ERAN and Marabou. We perform evaluation of the tool using an NLP dataset R-U-A-Robot suggested as a benchmark for verifying legally critical NLP applications. We hope that, thanks to its general applicability, this work will open novel possibilities for including NLP verification problems into neural network verification competitions, and will popularise NLP problems within this community.

Neural Network Verification with Proof Production

Deep neural networks (DNNs) are increasingly being employed in safety-critical systems, and there is an urgent need to guarantee their correctness. Consequently, the verification community has devised multiple techniques and tools for verifying DNNs. When DNN verifiers discover an input that triggers an error, that is easy to confirm; but when they report that no error exists, there is no way to ensure that the verification tool itself is not flawed. As multiple errors have already been observed in DNN verification tools, this calls the applicability of DNN verification into question. In this work, we present a novel mechanism for enhancing Simplex-based DNN verifiers with proof production capabilities: the generation of an easy-to-check witness of unsatisfiability, which attests to the absence of errors. Our proof production is based on an efficient adaptation of the well-known Farkas' lemma, combined with mechanisms for handling piecewise-linear functions and numerical precision errors. As a proof of concept, we implemented our technique on top of the Marabou DNN verifier. Our evaluation on a safety-critical system for airborne collision avoidance shows that proof production succeeds in almost all cases and requires only minimal overhead.