Abstraction-Based Proof Production in Formal Verification of Neural Networks

Modern verification tools for deep neural networks (DNNs) increasingly rely on abstraction to scale to realistic architectures. In parallel, proof production is becoming a critical requirement for increasing the reliability of DNN verification results. However, current proofproducing verifiers do not support abstraction-based reasoning, creating a gap between scalability and provable guarantees. We address this gap by introducing a novel framework for proof-producing abstraction-based DNN verification. Our approach modularly separates the verification task into two components: (i) proving the correctness of an abstract network, and (ii) proving the soundness of the abstraction with respect to the original DNN. The former can be handled by existing proof-producing verifiers, whereas we propose the first method for generating formal proofs for the latter. This preliminary work aims to enable scalable and trustworthy verification by supporting common abstraction techniques within a formal proof framework.

Explaining, Fast and Slow: Abstraction and Refinement of Provable Explanations

Despite significant advancements in post-hoc explainability techniques for neural networks, many current methods rely on heuristics and do not provide formally provable guarantees over the explanations provided. Recent work has shown that it is possible to obtain explanations with formal guarantees by identifying subsets of input features that are sufficient to determine that predictions remain unchanged using neural network verification techniques. Despite the appeal of these explanations, their computation faces significant scalability challenges. In this work, we address this gap by proposing a novel abstraction-refinement technique for efficiently computing provably sufficient explanations of neural network predictions. Our method abstracts the original large neural network by constructing a substantially reduced network, where a sufficient explanation of the reduced network is also provably sufficient for the original network, hence significantly speeding up the verification process. If the explanation is in sufficient on the reduced network, we iteratively refine the network size by gradually increasing it until convergence. Our experiments demonstrate that our approach enhances the efficiency of obtaining provably sufficient explanations for neural network predictions while additionally providing a fine-grained interpretation of the network's predictions across different abstraction levels.

Out of the Shadows: Exploring a Latent Space for Neural Network Verification

Neural networks are ubiquitous. However, they are often sensitive to small input changes. Hence, to prevent unexpected behavior in safety-critical applications, their formal verification -- a notoriously hard problem -- is necessary. Many state-of-the-art verification algorithms use reachability analysis or abstract interpretation to enclose the set of possible outputs of a neural network. Often, the verification is inconclusive due to the conservatism of the enclosure. To address this problem, we design a novel latent space for formal verification that enables the transfer of output specifications to the input space for an iterative specification-driven input refinement, i.e., we iteratively reduce the set of possible inputs to only enclose the unsafe ones. The latent space is constructed from a novel view of projection-based set representations, e.g., zonotopes, which are commonly used in reachability analysis of neural networks. A projection-based set representation is a "shadow" of a higher-dimensional set -- a latent space -- that does not change during a set propagation through a neural network. Hence, the input set and the output enclosure are "shadows" of the same latent space that we can use to transfer constraints. We present an efficient verification tool for neural networks that uses our iterative refinement to significantly reduce the number of subproblems in a branch-and-bound procedure. Using zonotopes as a set representation, unlike many other state-of-the-art approaches, our approach can be realized by only using matrix operations, which enables a significant speed-up through efficient GPU acceleration. We demonstrate that our tool achieves competitive performance, which would place it among the top-ranking tools of the last neural network verification competition (VNN-COMP'24).

Language Models That Walk the Talk: A Framework for Formal Fairness Certificates

As large language models become integral to high-stakes applications, ensuring their robustness and fairness is critical. Despite their success, large language models remain vulnerable to adversarial attacks, where small perturbations, such as synonym substitutions, can alter model predictions, posing risks in fairness-critical areas, such as gender bias mitigation, and safety-critical areas, such as toxicity detection. While formal verification has been explored for neural networks, its application to large language models remains limited. This work presents a holistic verification framework to certify the robustness of transformer-based language models, with a focus on ensuring gender fairness and consistent outputs across different gender-related terms. Furthermore, we extend this methodology to toxicity detection, offering formal guarantees that adversarially manipulated toxic inputs are consistently detected and appropriately censored, thereby ensuring the reliability of moderation systems. By formalizing robustness within the embedding space, this work strengthens the reliability of language models in ethical AI deployment and content moderation.

Training Verifiably Robust Agents Using Set-Based Reinforcement Learning

Reinforcement learning often uses neural networks to solve complex control tasks. However, neural networks are sensitive to input perturbations, which makes their deployment in safety-critical environments challenging. This work lifts recent results from formally verifying neural networks against such disturbances to reinforcement learning in continuous state and action spaces using reachability analysis. While previous work mainly focuses on adversarial attacks for robust reinforcement learning, we train neural networks utilizing entire sets of perturbed inputs and maximize the worst-case reward. The obtained agents are verifiably more robust than agents obtained by related work, making them more applicable in safety-critical environments. This is demonstrated with an extensive empirical evaluation of four different benchmarks.

Formal Verification of Graph Convolutional Networks with Uncertain Node Features and Uncertain Graph Structure

Graph neural networks are becoming increasingly popular in the field of machine learning due to their unique ability to process data structured in graphs. They have also been applied in safety-critical environments where perturbations inherently occur. However, these perturbations require us to formally verify neural networks before their deployment in safety-critical environments as neural networks are prone to adversarial attacks. While there exists research on the formal verification of neural networks, there is no work verifying the robustness of generic graph convolutional network architectures with uncertainty in the node features and in the graph structure over multiple message-passing steps. This work addresses this research gap by explicitly preserving the non-convex dependencies of all elements in the underlying computations through reachability analysis with (matrix) polynomial zonotopes. We demonstrate our approach on three popular benchmark datasets.

End-To-End Set-Based Training for Neural Network Verification

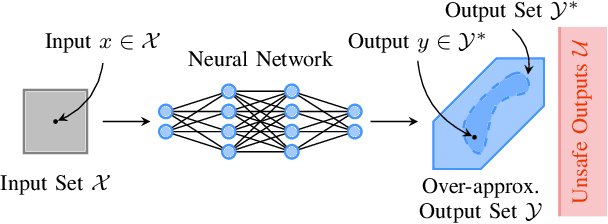
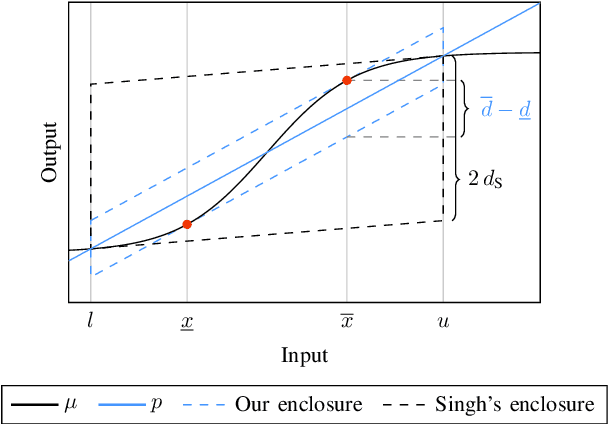
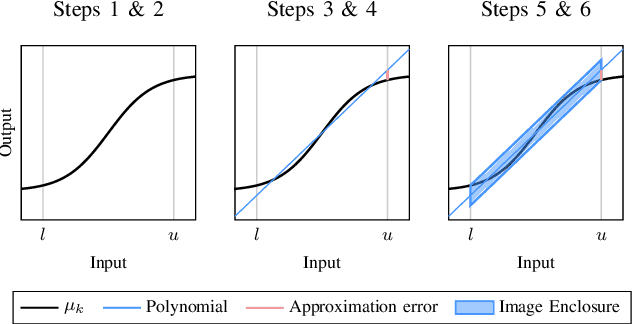
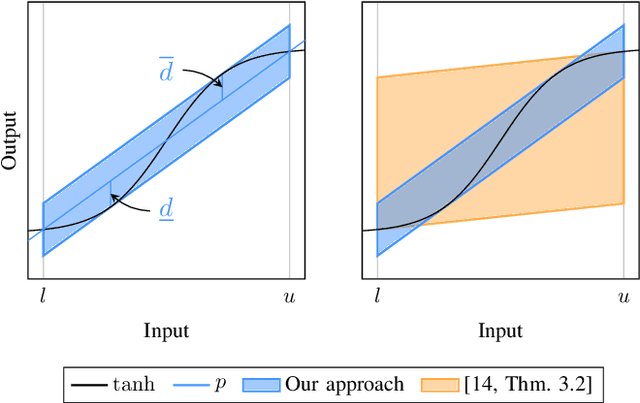
Neural networks are vulnerable to adversarial attacks, i.e., small input perturbations can result in substantially different outputs of a neural network. Safety-critical environments require neural networks that are robust against input perturbations. However, training and formally verifying robust neural networks is challenging. We address this challenge by employing, for the first time, a end-to-end set-based training procedure that trains robust neural networks for formal verification. Our training procedure drastically simplifies the subsequent formal robustness verification of the trained neural network. While previous research has predominantly focused on augmenting neural network training with adversarial attacks, our approach leverages set-based computing to train neural networks with entire sets of perturbed inputs. Moreover, we demonstrate that our set-based training procedure effectively trains robust neural networks, which are easier to verify. In many cases, set-based trained neural networks outperform neural networks trained with state-of-the-art adversarial attacks.

Specification-Driven Neural Network Reduction for Scalable Formal Verification

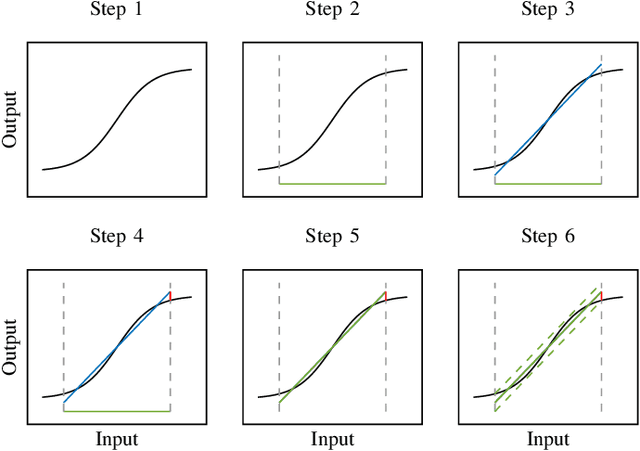
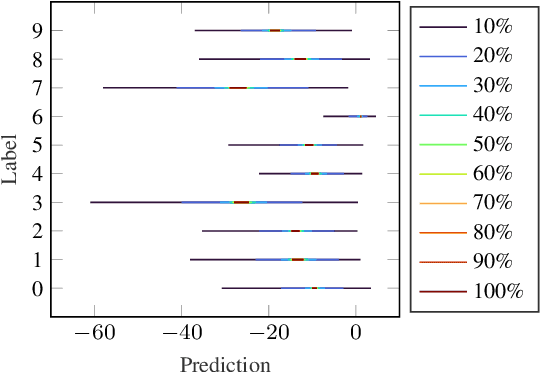
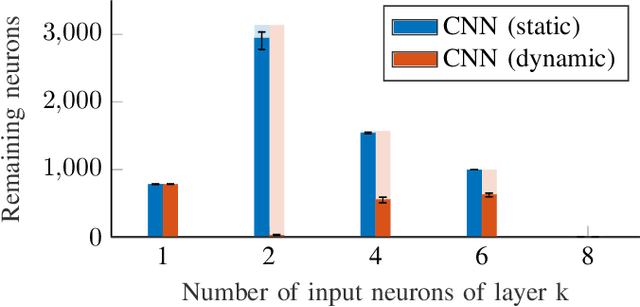
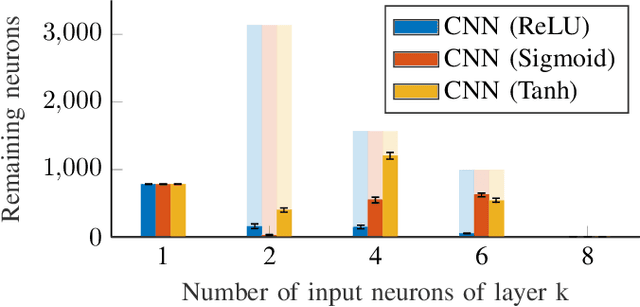
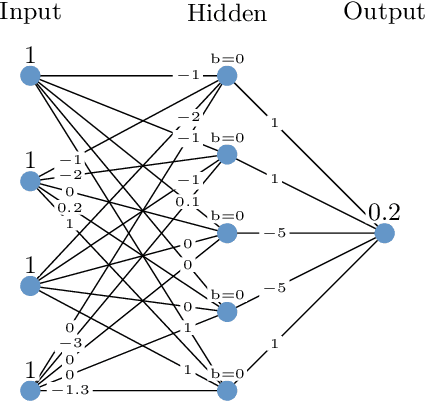
Formal verification of neural networks is essential before their deployment in safety-critical settings. However, existing methods for formally verifying neural networks are not yet scalable enough to handle practical problems that involve a large number of neurons. In this work, we propose a novel approach to address this challenge: A conservative neural network reduction approach that ensures that the verification of the reduced network implies the verification of the original network. Our approach constructs the reduction on-the-fly, while simultaneously verifying the original network and its specifications. The reduction merges all neurons of a nonlinear layer with similar outputs and is applicable to neural networks with any type of activation function such as ReLU, sigmoid, and tanh. Our evaluation shows that our approach can reduce a network to less than 5% of the number of neurons and thus to a similar degree the verification time is reduced.