A Generalised Framework for Property-Driven Machine Learning

Neural networks have been shown to frequently fail to satisfy critical safety and correctness properties after training, highlighting the pressing need for training methods that incorporate such properties directly. While adversarial training can be used to improve robustness to small perturbations within $\epsilon$-cubes, domains other than computer vision -- such as control systems and natural language processing -- may require more flexible input region specifications via generalised hyper-rectangles. Meanwhile, differentiable logics offer a way to encode arbitrary logical constraints as additional loss terms that guide the learning process towards satisfying these constraints. In this paper, we investigate how these two complementary approaches can be unified within a single framework for property-driven machine learning. We show that well-known properties from the literature are subcases of this general approach, and we demonstrate its practical effectiveness on a case study involving a neural network controller for a drone system. Our framework is publicly available at https://github.com/tflinkow/property-driven-ml.

Neural Network Verification for Gliding Drone Control: A Case Study

As machine learning is increasingly deployed in autonomous systems, verification of neural network controllers is becoming an active research domain. Existing tools and annual verification competitions suggest that soon this technology will become effective for real-world applications. Our application comes from the emerging field of microflyers that are passively transported by the wind, which may have various uses in weather or pollution monitoring. Specifically, we investigate centimetre-scale bio-inspired gliding drones that resemble Alsomitra macrocarpa diaspores. In this paper, we propose a new case study on verifying Alsomitra-inspired drones with neural network controllers, with the aim of adhering closely to a target trajectory. We show that our system differs substantially from existing VNN and ARCH competition benchmarks, and show that a combination of tools holds promise for verifying such systems in the future, if certain shortcomings can be overcome. We propose a novel method for robust training of regression networks, and investigate formalisations of this case study in Vehicle and CORA. Our verification results suggest that the investigated training methods do improve performance and robustness of neural network controllers in this application, but are limited in scope and usefulness. This is due to systematic limitations of both Vehicle and CORA, and the complexity of our system reducing the scale of reachability, which we investigate in detail. If these limitations can be overcome, it will enable engineers to develop safe and robust technologies that improve people's lives and reduce our impact on the environment.

NLP Verification: Towards a General Methodology for Certifying Robustness

Deep neural networks have exhibited substantial success in the field of Natural Language Processing (NLP) and ensuring their safety and reliability is crucial: there are safety critical contexts where such models must be robust to variability or attack, and give guarantees over their output. Unlike Computer Vision, NLP lacks a unified verification methodology and, despite recent advancements in literature, they are often light on the pragmatical issues of NLP verification. In this paper, we make an attempt to distil and evaluate general components of an NLP verification pipeline, that emerges from the progress in the field to date. Our contributions are two-fold. Firstly, we give a general characterisation of verifiable subspaces that result from embedding sentences into continuous spaces. We identify, and give an effective method to deal with, the technical challenge of semantic generalisability of verified subspaces; and propose it as a standard metric in the NLP verification pipelines (alongside with the standard metrics of model accuracy and model verifiability). Secondly, we propose a general methodology to analyse the effect of the embedding gap, a problem that refers to the discrepancy between verification of geometric subpspaces on the one hand, and semantic meaning of sentences which the geometric subspaces are supposed to represent, on the other hand. In extreme cases, poor choices in embedding of sentences may invalidate verification results. We propose a number of practical NLP methods that can help to identify the effects of the embedding gap; and in particular we propose the metric of falsifiability of semantic subpspaces as another fundamental metric to be reported as part of the NLP verification pipeline. We believe that together these general principles pave the way towards a more consolidated and effective development of this new domain.

ANTONIO: Towards a Systematic Method of Generating NLP Benchmarks for Verification

Verification of machine learning models used in Natural Language Processing (NLP) is known to be a hard problem. In particular, many known neural network verification methods that work for computer vision and other numeric datasets do not work for NLP. Here, we study technical reasons that underlie this problem. Based on this analysis, we propose practical methods and heuristics for preparing NLP datasets and models in a way that renders them amenable to known verification methods based on abstract interpretation. We implement these methods as a Python library called ANTONIO that links to the neural network verifiers ERAN and Marabou. We perform evaluation of the tool using an NLP dataset R-U-A-Robot suggested as a benchmark for verifying legally critical NLP applications. We hope that, thanks to its general applicability, this work will open novel possibilities for including NLP verification problems into neural network verification competitions, and will popularise NLP problems within this community.

Why Robust Natural Language Understanding is a Challenge

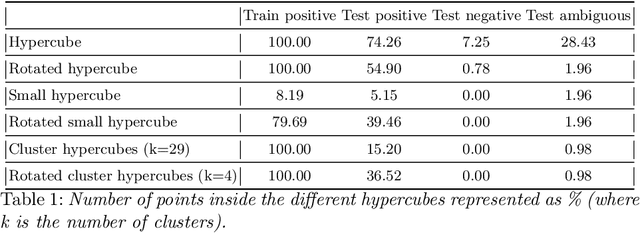
With the proliferation of Deep Machine Learning into real-life applications, a particular property of this technology has been brought to attention: Neural Networks notoriously present low robustness and can be highly sensitive to small input perturbations. Recently, many methods for verifying networks' general properties of robustness have been proposed, but they are mostly applied in Computer Vision. In this paper we propose a Verification method for Natural Language Understanding classification based on larger regions of interest, and we discuss the challenges of such task. We observe that, although the data is almost linearly separable, the verifier does not output positive results and we explain the problems and implications.

Property-driven Training: All You Ever Wanted to Know About

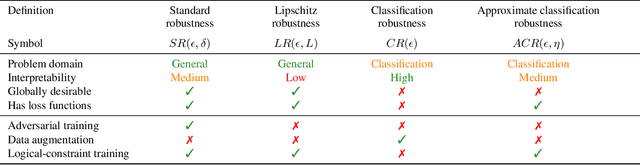
Neural networks are known for their ability to detect general patterns in noisy data. This makes them a popular tool for perception components in complex AI systems. Paradoxically, they are also known for being vulnerable to adversarial attacks. In response, various methods such as adversarial training, data-augmentation and Lipschitz robustness training have been proposed as means of improving their robustness. However, as this paper explores, these training methods each optimise for a different definition of robustness. We perform an in-depth comparison of these different definitions, including their relationship, assumptions, interpretability and verifiability after training. We also look at constraint-driven training, a general approach designed to encode arbitrary constraints, and show that not all of these definitions are directly encodable. Finally we perform experiments to compare the applicability and efficacy of the training methods at ensuring the network obeys these different definitions. These results highlight that even the encoding of such a simple piece of knowledge such as robustness in neural network training is fraught with difficult choices and pitfalls.