Marabou 2.0: A Versatile Formal Analyzer of Neural Networks

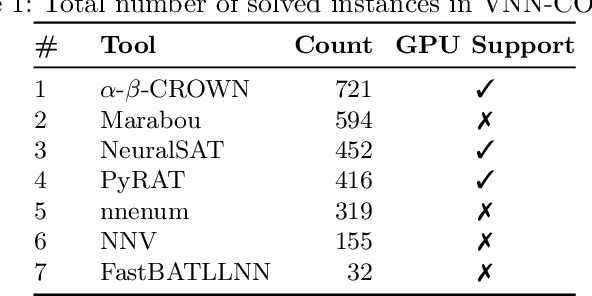
This paper serves as a comprehensive system description of version 2.0 of the Marabou framework for formal analysis of neural networks. We discuss the tool's architectural design and highlight the major features and components introduced since its initial release.

Efficient Neural Network Analysis with Sum-of-Infeasibilities

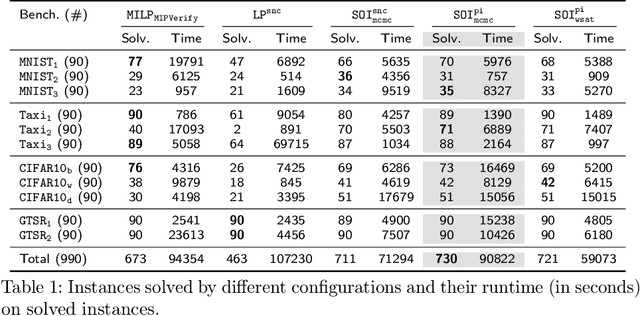
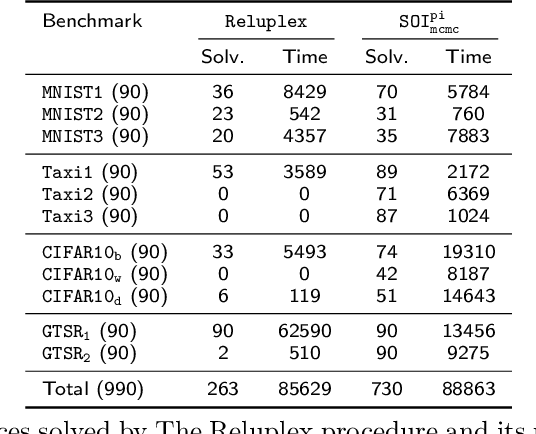
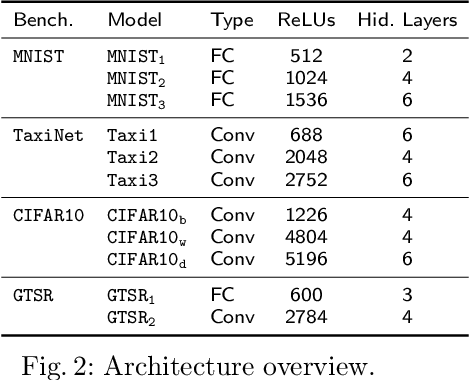
Inspired by sum-of-infeasibilities methods in convex optimization, we propose a novel procedure for analyzing verification queries on neural networks with piecewise-linear activation functions. Given a convex relaxation which over-approximates the non-convex activation functions, we encode the violations of activation functions as a cost function and optimize it with respect to the convex relaxation. The cost function, referred to as the Sum-of-Infeasibilities (SoI), is designed so that its minimum is zero and achieved only if all the activation functions are satisfied. We propose a stochastic procedure, DeepSoI, to efficiently minimize the SoI. An extension to a canonical case-analysis-based complete search procedure can be achieved by replacing the convex procedure executed at each search state with DeepSoI. Extending the complete search with DeepSoI achieves multiple simultaneous goals: 1) it guides the search towards a counter-example; 2) it enables more informed branching decisions; and 3) it creates additional opportunities for bound derivation. An extensive evaluation across different benchmarks and solvers demonstrates the benefit of the proposed techniques. In particular, we demonstrate that SoI significantly improves the performance of an existing complete search procedure. Moreover, the SoI-based implementation outperforms other state-of-the-art complete verifiers. We also show that our technique can efficiently improve upon the perturbation bound derived by a recent adversarial attack algorithm.

Global Optimization of Objective Functions Represented by ReLU Networks

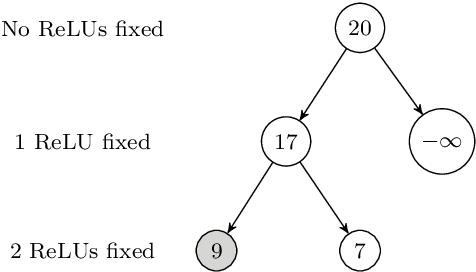
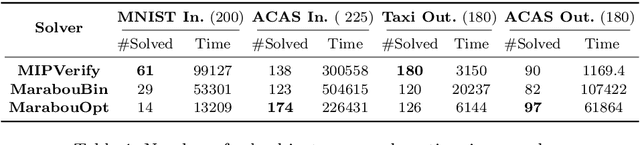
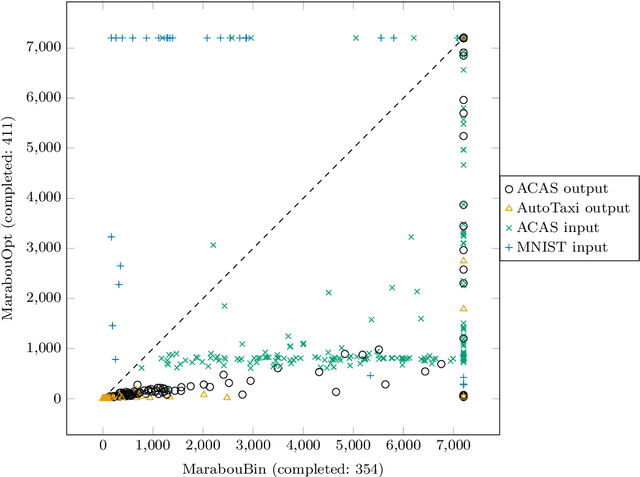
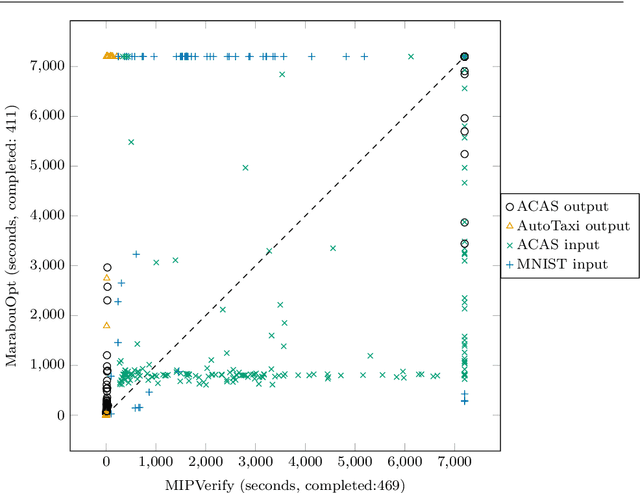
Neural networks (NN) learn complex non-convex functions, making them desirable solutions in many contexts. Applying NNs to safety-critical tasks demands formal guarantees about their behavior. Recently, a myriad of verification solutions for NNs emerged using reachability, optimization, and search based techniques. Particularly interesting are adversarial examples, which reveal ways the network can fail. They are widely generated using incomplete methods, such as local optimization, which cannot guarantee optimality. We propose strategies to extend existing verifiers to provide provably optimal adversarial examples. Naive approaches combine bisection search with an off-the-shelf verifier, resulting in many expensive calls to the verifier. Instead, our proposed approach yields tightly integrated optimizers, achieving better runtime performance. We extend Marabou, an SMT-based verifier, and compare it with the bisection based approach and MIPVerify, an optimization based verifier.

Parallelization Techniques for Verifying Neural Networks

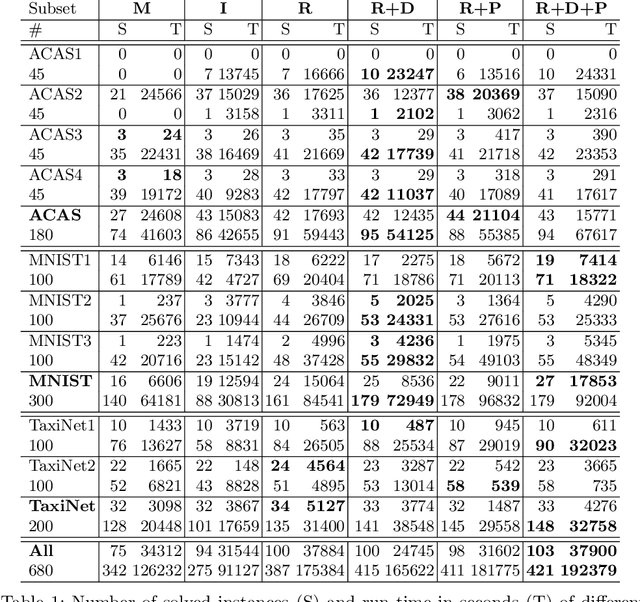
Inspired by recent successes with parallel optimization techniques for solving Boolean satisfiability, we investigate a set of strategies and heuristics that aim to leverage parallel computing to improve the scalability of neural network verification. We introduce an algorithm based on partitioning the verification problem in an iterative manner and explore two partitioning strategies, that work by partitioning the input space or by case splitting on the phases of the neuron activations, respectively. We also introduce a highly parallelizable pre-processing algorithm that uses the neuron activation phases to simplify the neural network verification problems. An extensive experimental evaluation shows the benefit of these techniques on both existing benchmarks and new benchmarks from the aviation domain. A preliminary experiment with ultra-scaling our algorithm using a large distributed cloud-based platform also shows promising results.