Udayan Mandal
Safe and Reliable Training of Learning-Based Aerospace Controllers
Jul 09, 2024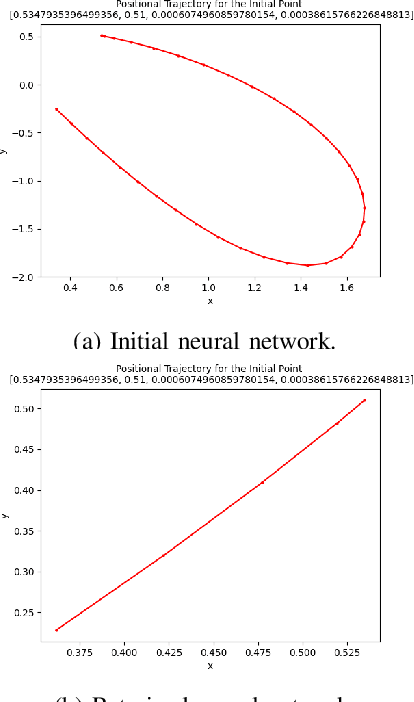


Abstract:In recent years, deep reinforcement learning (DRL) approaches have generated highly successful controllers for a myriad of complex domains. However, the opaque nature of these models limits their applicability in aerospace systems and safety-critical domains, in which a single mistake can have dire consequences. In this paper, we present novel advancements in both the training and verification of DRL controllers, which can help ensure their safe behavior. We showcase a design-for-verification approach utilizing k-induction and demonstrate its use in verifying liveness properties. In addition, we also give a brief overview of neural Lyapunov Barrier certificates and summarize their capabilities on a case study. Finally, we describe several other novel reachability-based approaches which, despite failing to provide guarantees of interest, could be effective for verification of other DRL systems, and could be of further interest to the community.
Formally Verifying Deep Reinforcement Learning Controllers with Lyapunov Barrier Certificates
May 22, 2024
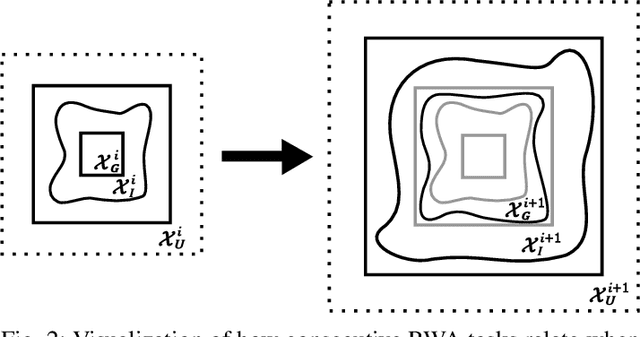
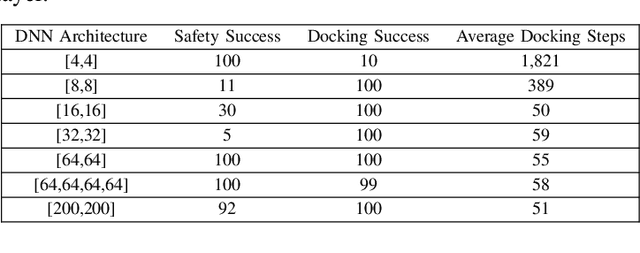
Abstract:Deep reinforcement learning (DRL) is a powerful machine learning paradigm for generating agents that control autonomous systems. However, the "black box" nature of DRL agents limits their deployment in real-world safety-critical applications. A promising approach for providing strong guarantees on an agent's behavior is to use Neural Lyapunov Barrier (NLB) certificates, which are learned functions over the system whose properties indirectly imply that an agent behaves as desired. However, NLB-based certificates are typically difficult to learn and even more difficult to verify, especially for complex systems. In this work, we present a novel method for training and verifying NLB-based certificates for discrete-time systems. Specifically, we introduce a technique for certificate composition, which simplifies the verification of highly-complex systems by strategically designing a sequence of certificates. When jointly verified with neural network verification engines, these certificates provide a formal guarantee that a DRL agent both achieves its goals and avoids unsafe behavior. Furthermore, we introduce a technique for certificate filtering, which significantly simplifies the process of producing formally verified certificates. We demonstrate the merits of our approach with a case study on providing safety and liveness guarantees for a DRL-controlled spacecraft.
Local Area Routes for Vehicle Routing Problems
Jul 10, 2022
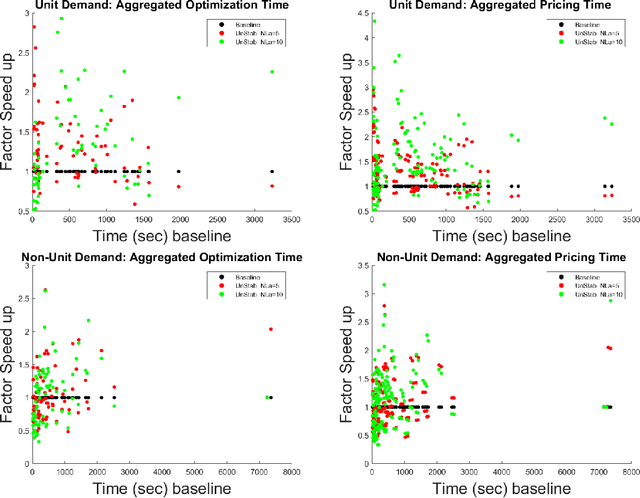
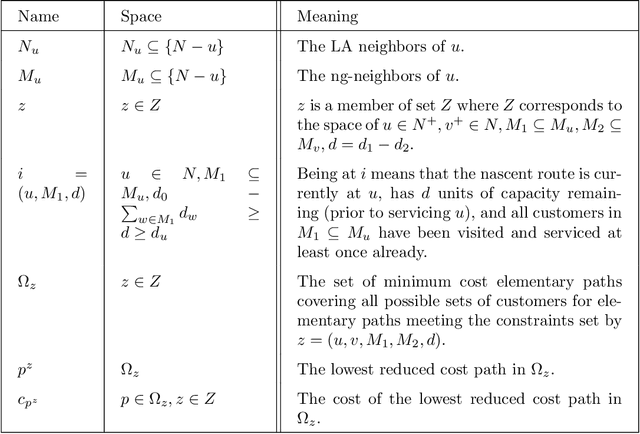
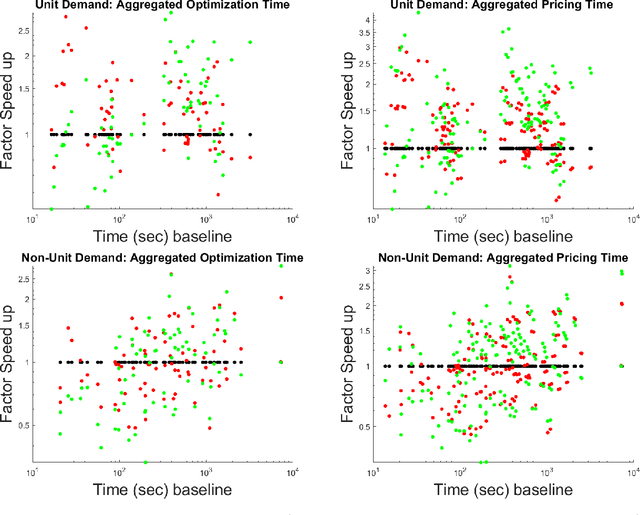
Abstract:We consider an approach for improving the efficiency of column generation (CG) methods for solving vehicle routing problems. We introduce Local Area (LA) route relaxations, an alternative/complement to the commonly used ng-route relaxations and Decremental State Space Relaxations (DSSR) inside of CG formulations. LA routes are a subset of ng-routes and a super-set of elementary routes. Normally, the pricing stage of CG must produce elementary routes, which are routes without repeated customers, using processes which can be computationally expensive. Non-elementary routes visit at least one customer more than once, creating a cycle. LA routes relax the constraint of being an elementary route in such a manner as to permit efficient pricing. LA routes are best understood in terms of ng-route relaxations. Ng-routes are routes which are permitted to have non-localized cycles in space; this means that at least one intermediate customer (called a breaker) in the cycle must consider the starting customer in the cycle to be spatially far away. LA routes are described using a set of special indexes corresponding to customers on the route ordered from the start to the end of the route. LA route relaxations further restrict the set of permitted cycles beyond that of ng-routes by additionally enforcing that the breaker must be a located at a special index where the set of special indexes is defined recursively as follows. The first special index in the route is at index 1 meaning that it is associated with the first customer in the route. The k'th special index corresponds to the first customer after the k-1'th special index, that is not considered to be a neighbor of (considered spatially far from) the customer located at the k-1'th special index. We demonstrate that LA route relaxations can significantly improve the computational speed of pricing when compared to the standard DSSR.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge