Local Area Routes for Vehicle Routing Problems

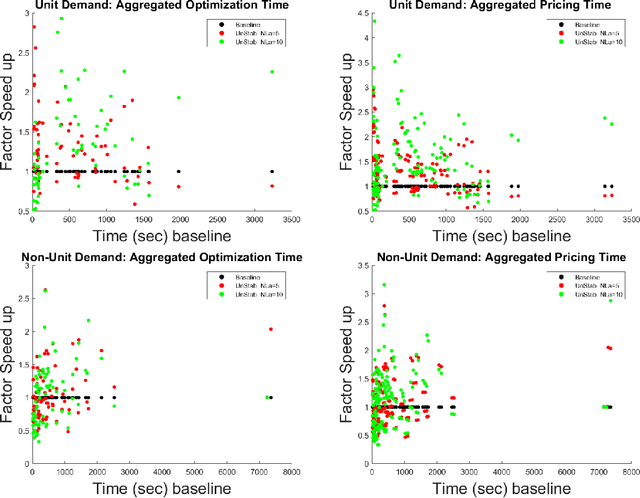
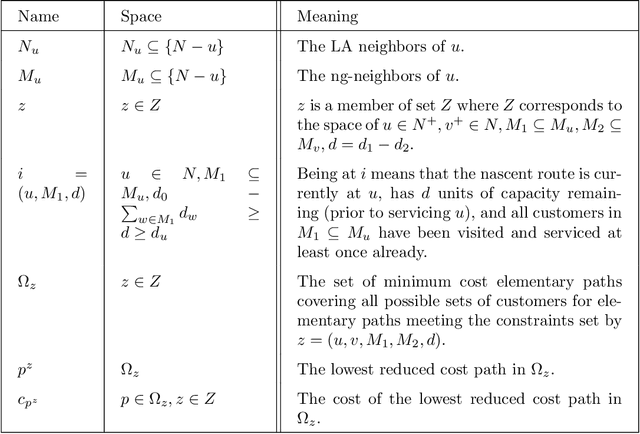
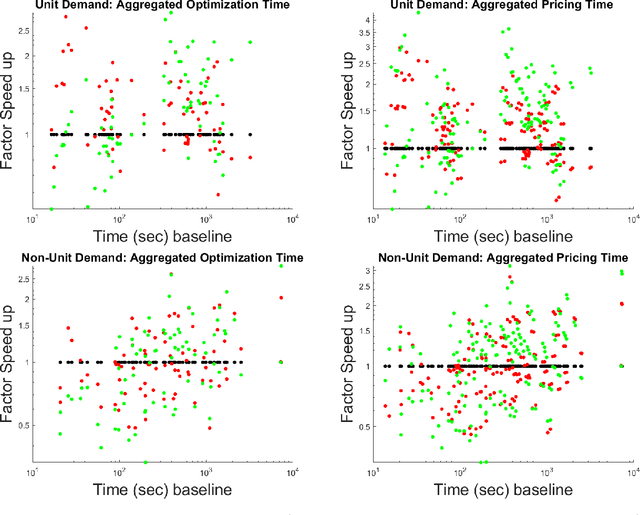
We consider an approach for improving the efficiency of column generation (CG) methods for solving vehicle routing problems. We introduce Local Area (LA) route relaxations, an alternative/complement to the commonly used ng-route relaxations and Decremental State Space Relaxations (DSSR) inside of CG formulations. LA routes are a subset of ng-routes and a super-set of elementary routes. Normally, the pricing stage of CG must produce elementary routes, which are routes without repeated customers, using processes which can be computationally expensive. Non-elementary routes visit at least one customer more than once, creating a cycle. LA routes relax the constraint of being an elementary route in such a manner as to permit efficient pricing. LA routes are best understood in terms of ng-route relaxations. Ng-routes are routes which are permitted to have non-localized cycles in space; this means that at least one intermediate customer (called a breaker) in the cycle must consider the starting customer in the cycle to be spatially far away. LA routes are described using a set of special indexes corresponding to customers on the route ordered from the start to the end of the route. LA route relaxations further restrict the set of permitted cycles beyond that of ng-routes by additionally enforcing that the breaker must be a located at a special index where the set of special indexes is defined recursively as follows. The first special index in the route is at index 1 meaning that it is associated with the first customer in the route. The k'th special index corresponds to the first customer after the k-1'th special index, that is not considered to be a neighbor of (considered spatially far from) the customer located at the k-1'th special index. We demonstrate that LA route relaxations can significantly improve the computational speed of pricing when compared to the standard DSSR.

Clustering of Time Series Data with Prior Geographical Information

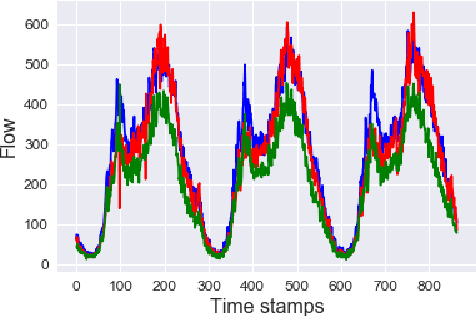
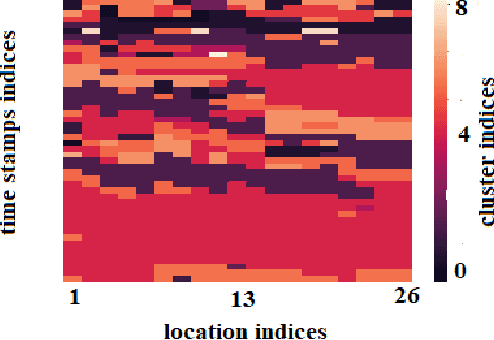
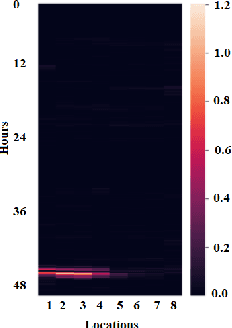
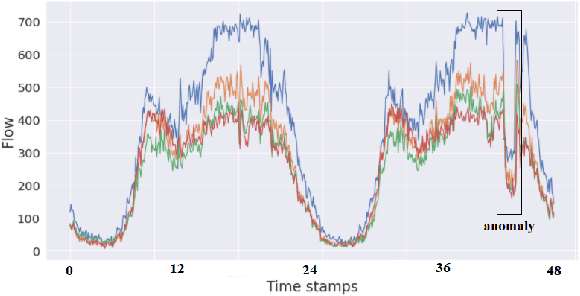
Time Series data are broadly studied in various domains of transportation systems. Traffic data area challenging example of spatio-temporal data, as it is multi-variate time series with high correlations in spatial and temporal neighborhoods. Spatio-temporal clustering of traffic flow data find similar patterns in both spatial and temporal domain, where it provides better capability for analyzing a transportation network, and improving related machine learning models, such as traffic flow prediction and anomaly detection. In this paper, we propose a spatio-temporal clustering model, where it clusters time series data based on spatial and temporal contexts. We propose a variation of a Deep Embedded Clustering(DEC) model for finding spatio-temporal clusters. The proposed model Spatial-DEC (S-DEC) use prior geographical information in building latent feature representations. We also define evaluation metrics for spatio-temporal clusters. Not only do the obtained clusters have better temporal similarity when evaluated using DTW distance, but also the clusters better represents spatial connectivity and dis-connectivity. We use traffic flow data obtained by PeMS in our analysis. The results show that the proposed Spatial-DEC can find more desired spatio-temporal clusters.

Multi-Robot Routing with Time Windows: A Column Generation Approach

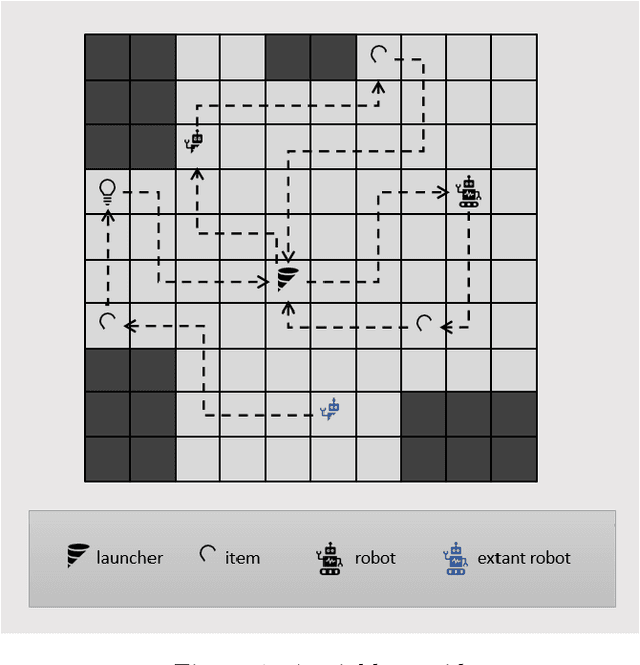
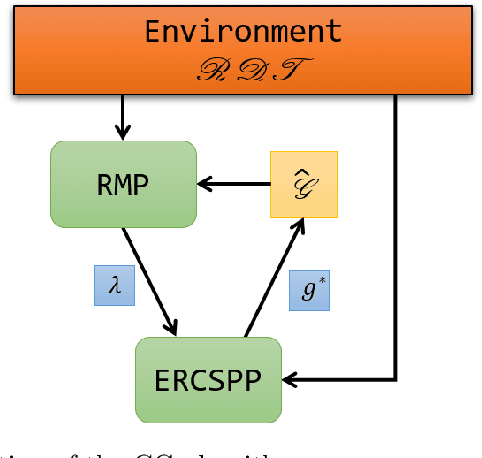
Robots performing tasks in warehouses provide the first example of wide-spread adoption of autonomous vehicles in transportation and logistics. The efficiency of these operations, which can vary widely in practice, are a key factor in the success of supply chains. In this work we consider the problem of coordinating a fleet of robots performing picking operations in a warehouse so as to maximize the net profit achieved within a time period while respecting problem- and robot-specific constraints. We formulate the problem as a weighted set packing problem where the elements in consideration are items on the warehouse floor that can be picked up and delivered within specified time windows. We enforce the constraint that robots must not collide, that each item is picked up and delivered by at most one robot, and that the number of robots active at any time does not exceed the total number available. Since the set of routes is exponential in the size of the input, we attack optimization of the resulting integer linear program using column generation, where pricing amounts to solving an elementary resource-constrained shortest-path problem. We propose an efficient optimization scheme that avoids consideration of every increment within the time windows. We also propose a heuristic pricing algorithm that can efficiently solve the pricing subproblem. While this itself is an important problem, the insights gained from solving these problems effectively can lead to new advances in other time-widow constrained vehicle routing problems.

A convolution recurrent autoencoder for spatio-temporal missing data imputation

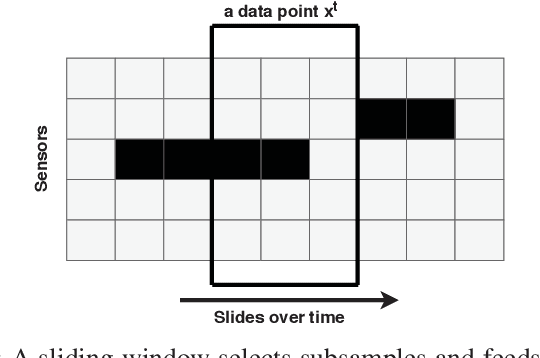
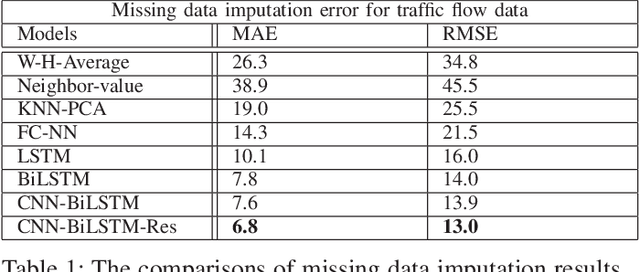
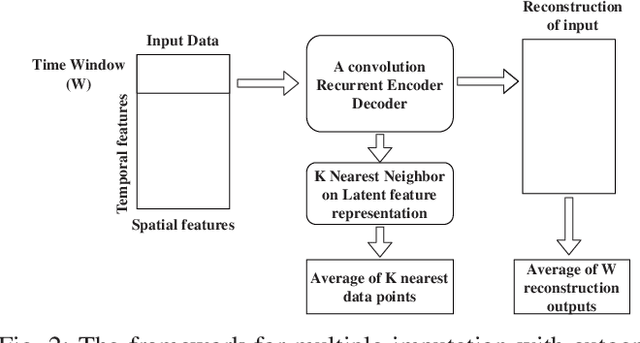
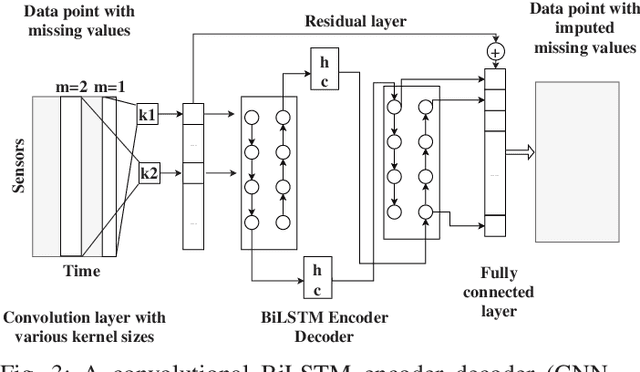
When sensors collect spatio-temporal data in a large geographical area, the existence of missing data cannot be escaped. Missing data negatively impacts the performance of data analysis and machine learning algorithms. In this paper, we study deep autoencoders for missing data imputation in spatio-temporal problems. We propose a convolution bidirectional-LSTM for capturing spatial and temporal patterns. Moreover, we analyze an autoencoder's latent feature representation in spatio-temporal data and illustrate its performance for missing data imputation. Traffic flow data are used for evaluation of our models. The result shows that the proposed convolution recurrent neural network outperforms state-of-the-art methods.

A Spatial-Temporal Decomposition Based Deep Neural Network for Time Series Forecasting

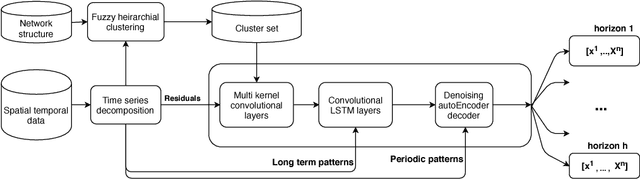
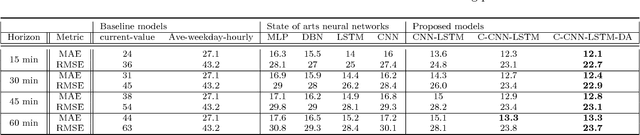
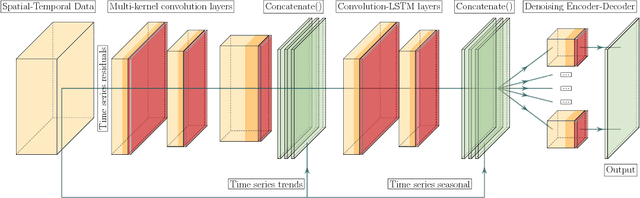
Spatial time series forecasting problems arise in a broad range of applications, such as environmental and transportation problems. These problems are challenging because of the existence of specific spatial, short-term and long-term patterns, and the curse of dimensionality. In this paper, we propose a deep neural network framework for large-scale spatial time series forecasting problems. We explicitly designed the neural network architecture for capturing various types of patterns. In preprocessing, a time series decomposition method is applied to separately feed short-term, long-term and spatial patterns into different components of a neural network. A fuzzy clustering method finds cluster of neighboring time series based on similarity of time series residuals; as they can be meaningful short-term patterns for spatial time series. In neural network architecture, each kernel of a multi-kernel convolution layer is applied to a cluster of time series to extract short-term features in neighboring areas. The output of convolution layer is concatenated by trends and followed by convolution-LSTM layer to capture long-term patterns in larger regional areas. To make a robust prediction when faced with missing data, an unsupervised pretrained denoising autoencoder reconstructs the output of the model in a fine-tuning step. The experimental results illustrate the model outperforms baseline and state of the art models in a traffic flow prediction dataset.

Thompson Sampling in Dynamic Systems for Contextual Bandit Problems

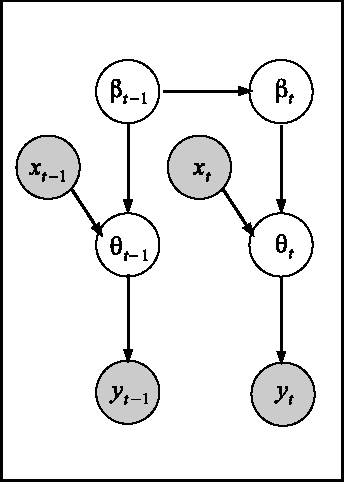
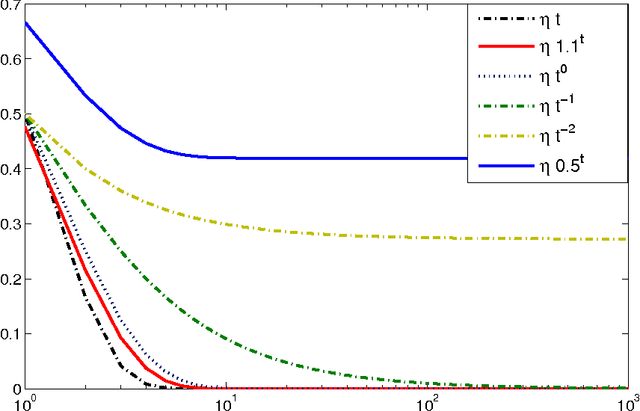
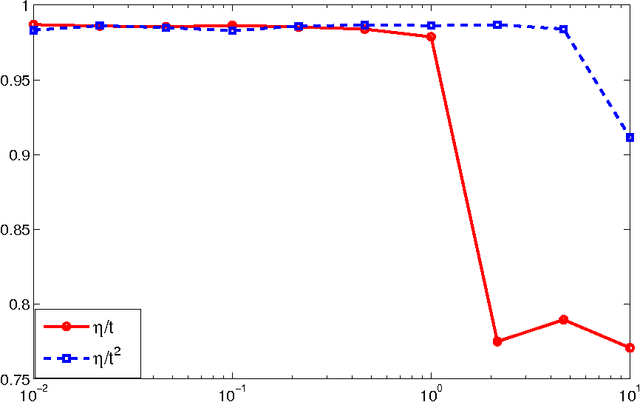
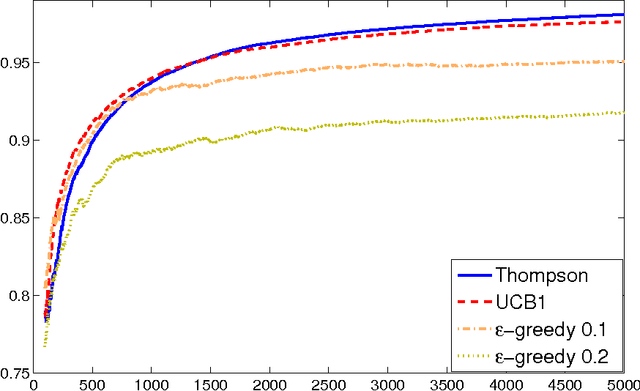
We consider the multiarm bandit problems in the timevarying dynamic system for rich structural features. For the nonlinear dynamic model, we propose the approximate inference for the posterior distributions based on Laplace Approximation. For the context bandit problems, Thompson Sampling is adopted based on the underlying posterior distributions of the parameters. More specifically, we introduce the discount decays on the previous samples impact and analyze the different decay rates with the underlying sample dynamics. Consequently, the exploration and exploitation is adaptively tradeoff according to the dynamics in the system.

Online Classification Using a Voted RDA Method

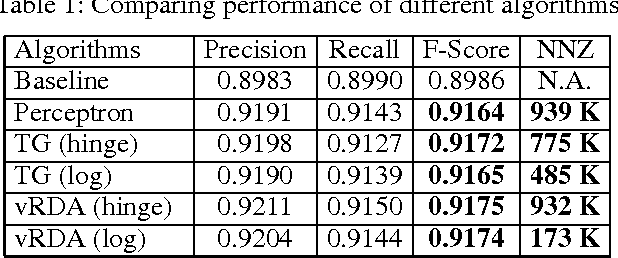
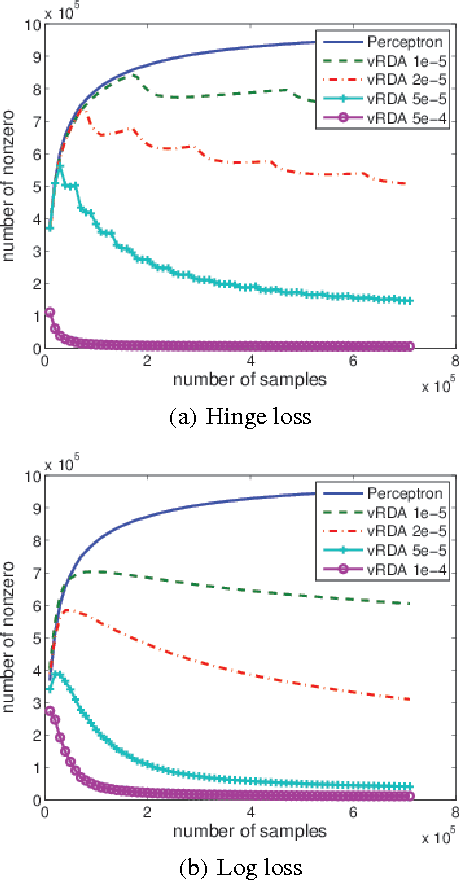
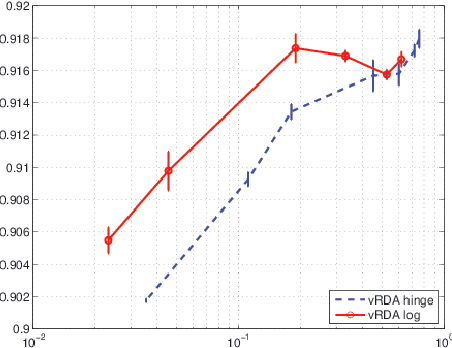
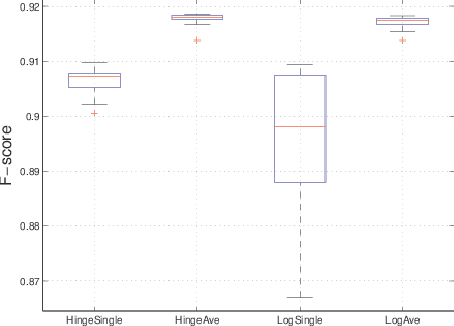
We propose a voted dual averaging method for online classification problems with explicit regularization. This method employs the update rule of the regularized dual averaging (RDA) method, but only on the subsequence of training examples where a classification error is made. We derive a bound on the number of mistakes made by this method on the training set, as well as its generalization error rate. We also introduce the concept of relative strength of regularization, and show how it affects the mistake bound and generalization performance. We experimented with the method using $\ell_1$ regularization on a large-scale natural language processing task, and obtained state-of-the-art classification performance with fairly sparse models.