Multi-Robot Routing with Time Windows: A Column Generation Approach

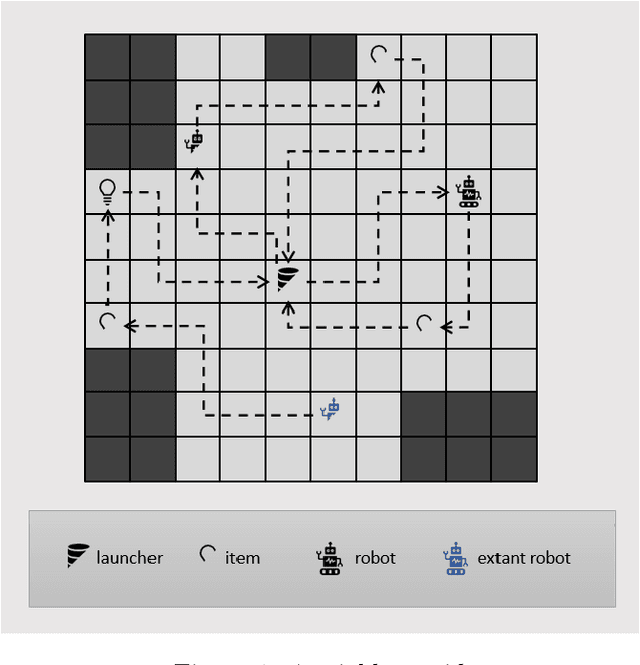
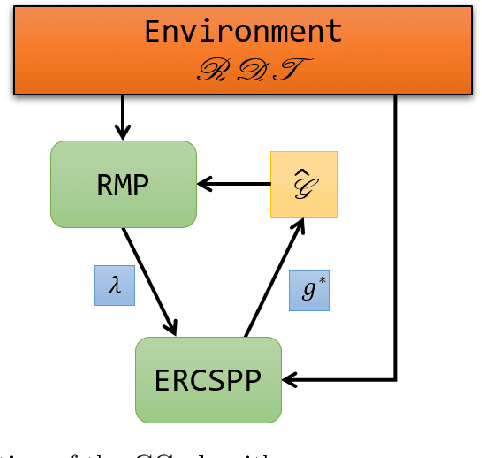
Robots performing tasks in warehouses provide the first example of wide-spread adoption of autonomous vehicles in transportation and logistics. The efficiency of these operations, which can vary widely in practice, are a key factor in the success of supply chains. In this work we consider the problem of coordinating a fleet of robots performing picking operations in a warehouse so as to maximize the net profit achieved within a time period while respecting problem- and robot-specific constraints. We formulate the problem as a weighted set packing problem where the elements in consideration are items on the warehouse floor that can be picked up and delivered within specified time windows. We enforce the constraint that robots must not collide, that each item is picked up and delivered by at most one robot, and that the number of robots active at any time does not exceed the total number available. Since the set of routes is exponential in the size of the input, we attack optimization of the resulting integer linear program using column generation, where pricing amounts to solving an elementary resource-constrained shortest-path problem. We propose an efficient optimization scheme that avoids consideration of every increment within the time windows. We also propose a heuristic pricing algorithm that can efficiently solve the pricing subproblem. While this itself is an important problem, the insights gained from solving these problems effectively can lead to new advances in other time-widow constrained vehicle routing problems.

Integer Programming for Multi-Robot Planning: A Column Generation Approach

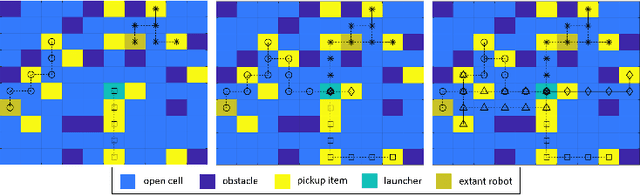
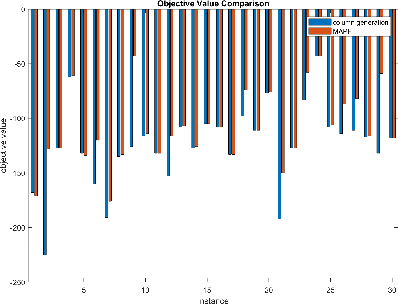
We consider the problem of coordinating a fleet of robots in a warehouse so as to maximize the reward achieved within a time limit while respecting problem and robot specific constraints. We formulate the problem as a weighted set packing problem where elements are defined as being the space-time positions a robot can occupy and the items that can be picked up and delivered. We enforce that robots do not collide, that each item is delivered at most once, and that the number of robots active at any time does not exceed the total number available. Since the set of robot routes is not enumerable, we attack optimization using column generation where pricing is a resource-constrained shortest-path problem.

Relaxed Dual Optimal Inequalities for Relaxed Columns: with Application to Vehicle Routing

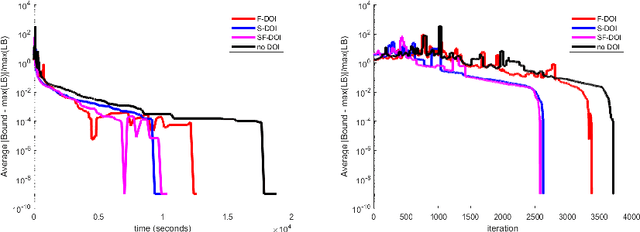
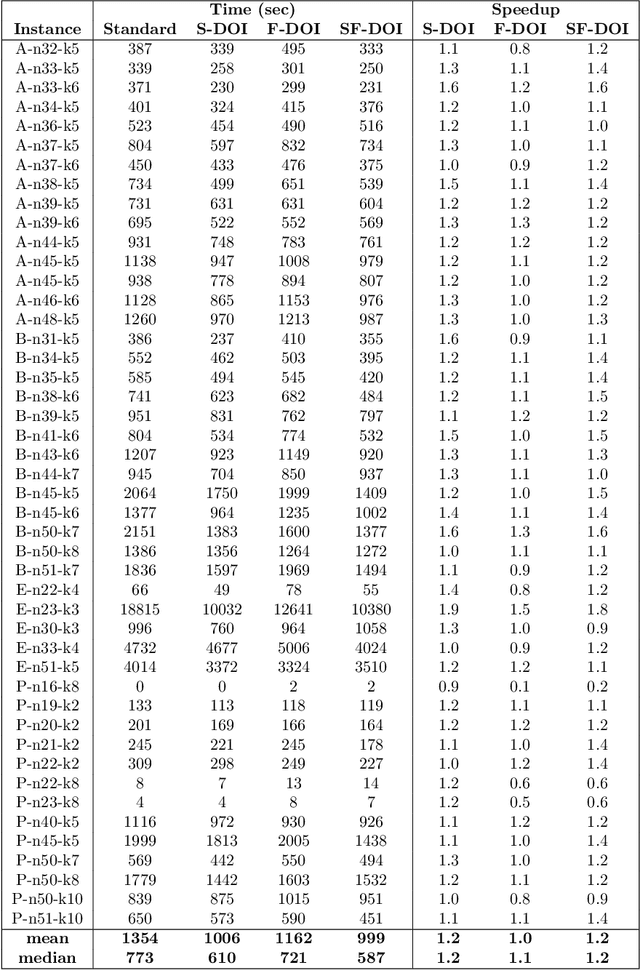
We address the problem of accelerating column generation for set cover problems in which we relax the state space of the columns to do efficient pricing. We achieve this by adapting the recently introduced smooth and flexible dual optimal inequalities (DOI) for use with relaxed columns. Smooth DOI exploit the observation that similar items are nearly fungible, and hence should be associated with similarly valued dual variables. Flexible DOI exploit the observation that the change in cost of a column induced by removing an item can be bounded. We adapt these DOI to the problem of capacitated vehicle routing in the context of ng-route relaxations. We demonstrate significant speed ups on a benchmark data set, while provably not weakening the relaxation.