Multi-Robot Routing with Time Windows: A Column Generation Approach
Paper and Code
Mar 16, 2021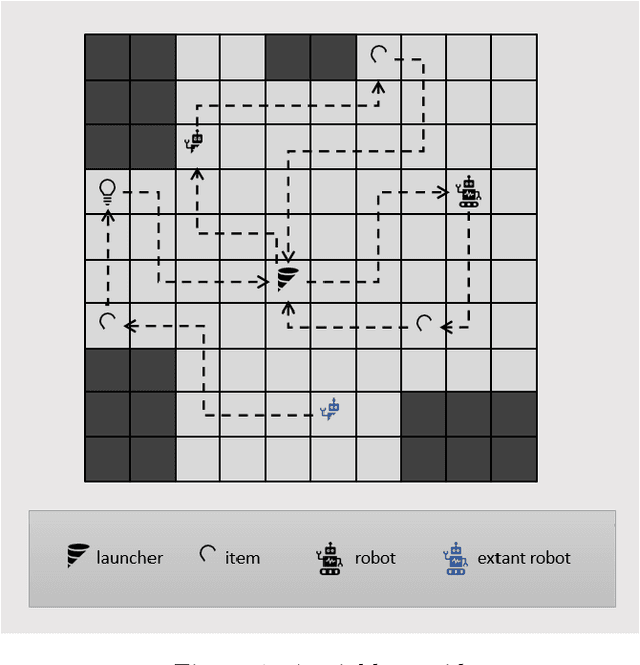

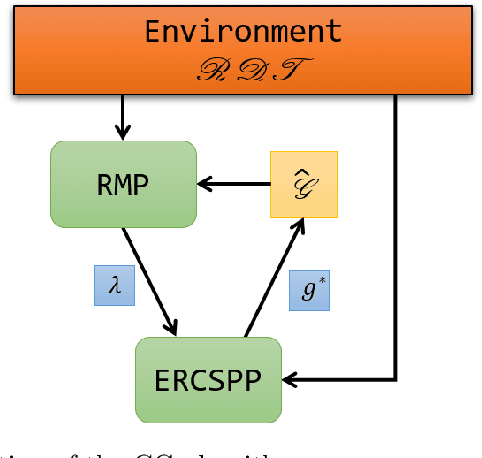

Robots performing tasks in warehouses provide the first example of wide-spread adoption of autonomous vehicles in transportation and logistics. The efficiency of these operations, which can vary widely in practice, are a key factor in the success of supply chains. In this work we consider the problem of coordinating a fleet of robots performing picking operations in a warehouse so as to maximize the net profit achieved within a time period while respecting problem- and robot-specific constraints. We formulate the problem as a weighted set packing problem where the elements in consideration are items on the warehouse floor that can be picked up and delivered within specified time windows. We enforce the constraint that robots must not collide, that each item is picked up and delivered by at most one robot, and that the number of robots active at any time does not exceed the total number available. Since the set of routes is exponential in the size of the input, we attack optimization of the resulting integer linear program using column generation, where pricing amounts to solving an elementary resource-constrained shortest-path problem. We propose an efficient optimization scheme that avoids consideration of every increment within the time windows. We also propose a heuristic pricing algorithm that can efficiently solve the pricing subproblem. While this itself is an important problem, the insights gained from solving these problems effectively can lead to new advances in other time-widow constrained vehicle routing problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge