Boosting Sample Efficiency and Generalization in Multi-agent Reinforcement Learning via Equivariance

Multi-Agent Reinforcement Learning (MARL) struggles with sample inefficiency and poor generalization [1]. These challenges are partially due to a lack of structure or inductive bias in the neural networks typically used in learning the policy. One such form of structure that is commonly observed in multi-agent scenarios is symmetry. The field of Geometric Deep Learning has developed Equivariant Graph Neural Networks (EGNN) that are equivariant (or symmetric) to rotations, translations, and reflections of nodes. Incorporating equivariance has been shown to improve learning efficiency and decrease error [ 2 ]. In this paper, we demonstrate that EGNNs improve the sample efficiency and generalization in MARL. However, we also show that a naive application of EGNNs to MARL results in poor early exploration due to a bias in the EGNN structure. To mitigate this bias, we present Exploration-enhanced Equivariant Graph Neural Networks or E2GN2. We compare E2GN2 to other common function approximators using common MARL benchmarks MPE and SMACv2. E2GN2 demonstrates a significant improvement in sample efficiency, greater final reward convergence, and a 2x-5x gain in over standard GNNs in our generalization tests. These results pave the way for more reliable and effective solutions in complex multi-agent systems.

Permutation Invariant Representations with Applications to Graph Deep Learning

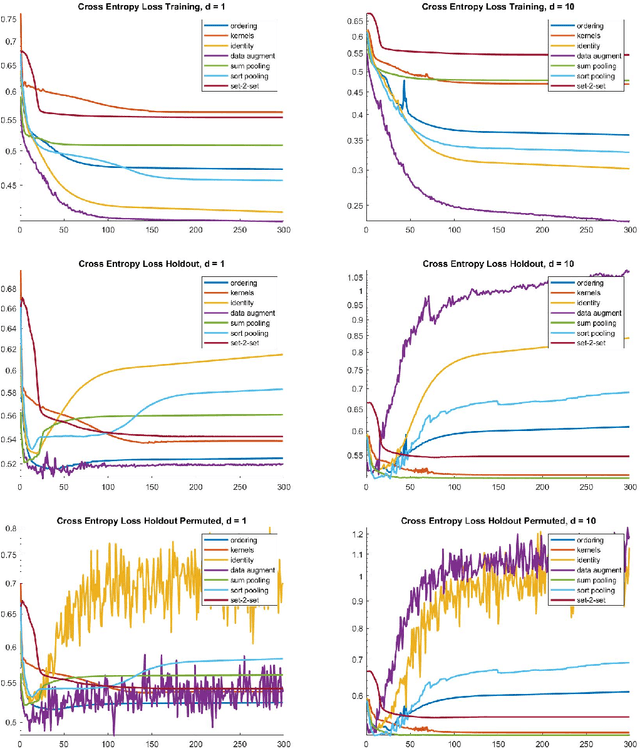
This paper presents primarily two Euclidean embeddings of the quotient space generated by matrices that are identified modulo arbitrary row permutations. The original application is in deep learning on graphs where the learning task is invariant to node relabeling. Two embedding schemes are introduced, one based on sorting and the other based on algebras of multivariate polynomials. While both embeddings exhibit a computational complexity exponential in problem size, the sorting based embedding is globally bi-Lipschitz and admits a low dimensional target space. Additionally, an almost everywhere injective scheme can be implemented with minimal redundancy and low computational cost. In turn, this proves that almost any classifier can be implemented with an arbitrary small loss of performance. Numerical experiments are carried out on two data sets, a chemical compound data set (QM9) and a proteins data set (PROTEINS).

Multi-Robot Routing with Time Windows: A Column Generation Approach

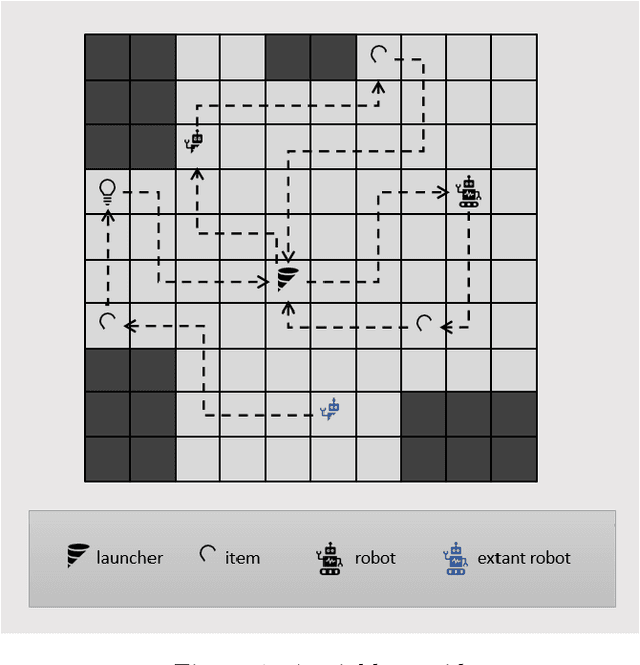
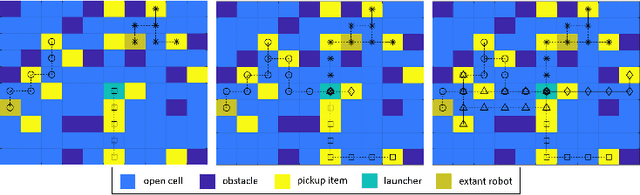
Robots performing tasks in warehouses provide the first example of wide-spread adoption of autonomous vehicles in transportation and logistics. The efficiency of these operations, which can vary widely in practice, are a key factor in the success of supply chains. In this work we consider the problem of coordinating a fleet of robots performing picking operations in a warehouse so as to maximize the net profit achieved within a time period while respecting problem- and robot-specific constraints. We formulate the problem as a weighted set packing problem where the elements in consideration are items on the warehouse floor that can be picked up and delivered within specified time windows. We enforce the constraint that robots must not collide, that each item is picked up and delivered by at most one robot, and that the number of robots active at any time does not exceed the total number available. Since the set of routes is exponential in the size of the input, we attack optimization of the resulting integer linear program using column generation, where pricing amounts to solving an elementary resource-constrained shortest-path problem. We propose an efficient optimization scheme that avoids consideration of every increment within the time windows. We also propose a heuristic pricing algorithm that can efficiently solve the pricing subproblem. While this itself is an important problem, the insights gained from solving these problems effectively can lead to new advances in other time-widow constrained vehicle routing problems.

Integer Programming for Multi-Robot Planning: A Column Generation Approach

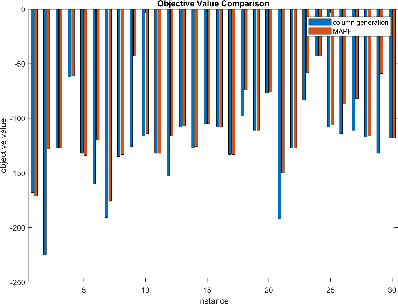
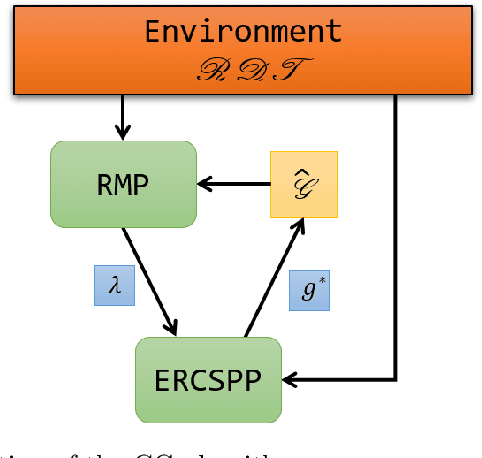
We consider the problem of coordinating a fleet of robots in a warehouse so as to maximize the reward achieved within a time limit while respecting problem and robot specific constraints. We formulate the problem as a weighted set packing problem where elements are defined as being the space-time positions a robot can occupy and the items that can be picked up and delivered. We enforce that robots do not collide, that each item is delivered at most once, and that the number of robots active at any time does not exceed the total number available. Since the set of robot routes is not enumerable, we attack optimization using column generation where pricing is a resource-constrained shortest-path problem.

Relaxed Dual Optimal Inequalities for Relaxed Columns: with Application to Vehicle Routing

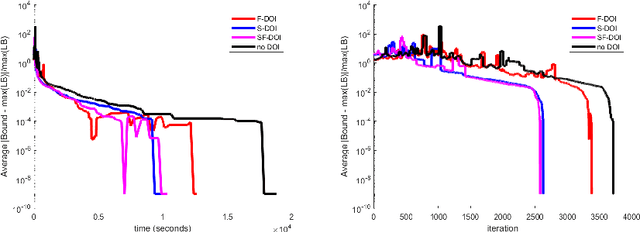
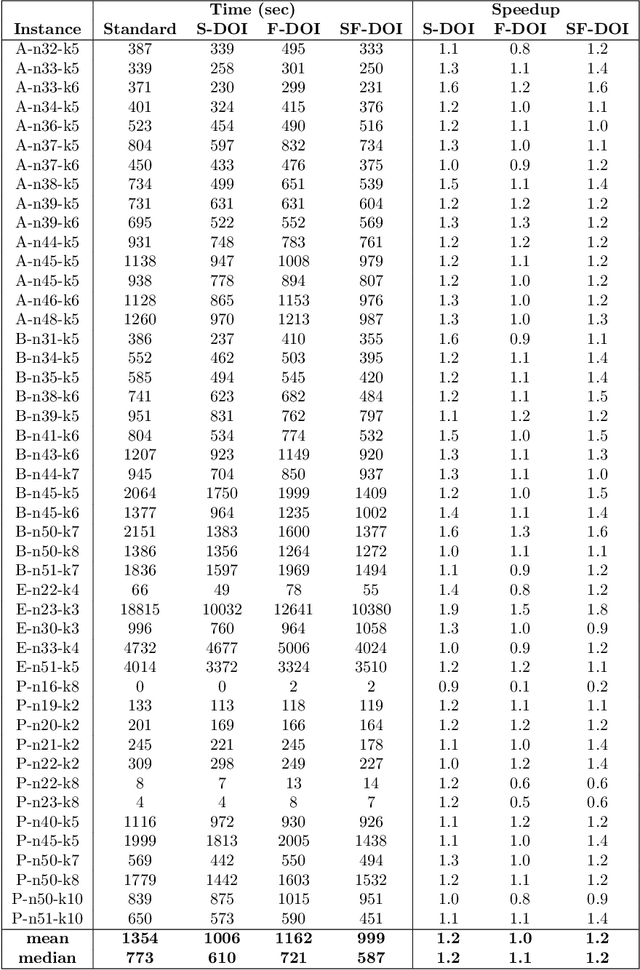
We address the problem of accelerating column generation for set cover problems in which we relax the state space of the columns to do efficient pricing. We achieve this by adapting the recently introduced smooth and flexible dual optimal inequalities (DOI) for use with relaxed columns. Smooth DOI exploit the observation that similar items are nearly fungible, and hence should be associated with similarly valued dual variables. Flexible DOI exploit the observation that the change in cost of a column induced by removing an item can be bounded. We adapt these DOI to the problem of capacitated vehicle routing in the context of ng-route relaxations. We demonstrate significant speed ups on a benchmark data set, while provably not weakening the relaxation.