Integer Programming for Multi-Robot Planning: A Column Generation Approach
Paper and Code
Jun 08, 2020

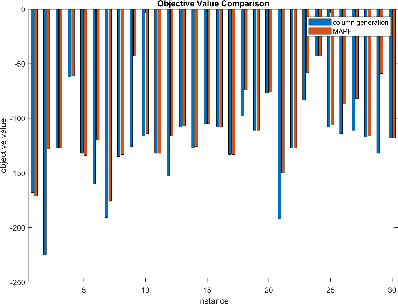
We consider the problem of coordinating a fleet of robots in a warehouse so as to maximize the reward achieved within a time limit while respecting problem and robot specific constraints. We formulate the problem as a weighted set packing problem where elements are defined as being the space-time positions a robot can occupy and the items that can be picked up and delivered. We enforce that robots do not collide, that each item is delivered at most once, and that the number of robots active at any time does not exceed the total number available. Since the set of robot routes is not enumerable, we attack optimization using column generation where pricing is a resource-constrained shortest-path problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge