Local Area Routes for Vehicle Routing Problems

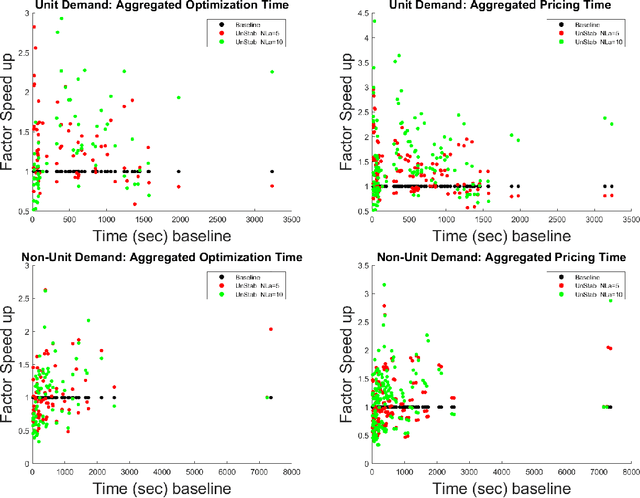
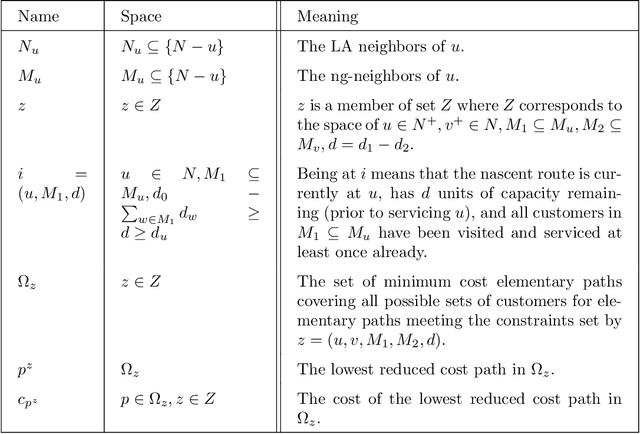
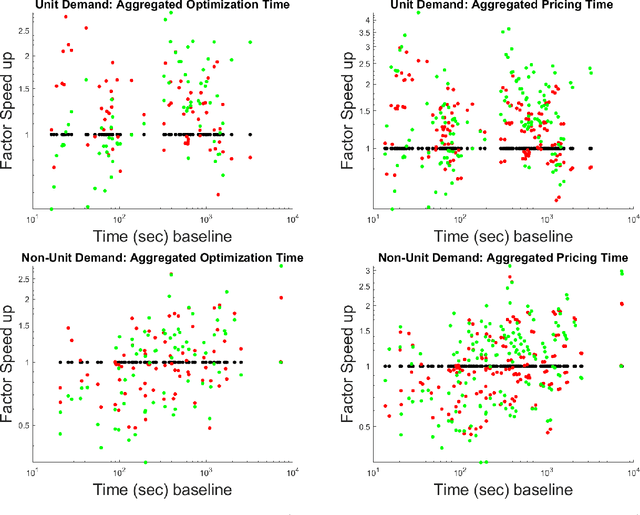
We consider an approach for improving the efficiency of column generation (CG) methods for solving vehicle routing problems. We introduce Local Area (LA) route relaxations, an alternative/complement to the commonly used ng-route relaxations and Decremental State Space Relaxations (DSSR) inside of CG formulations. LA routes are a subset of ng-routes and a super-set of elementary routes. Normally, the pricing stage of CG must produce elementary routes, which are routes without repeated customers, using processes which can be computationally expensive. Non-elementary routes visit at least one customer more than once, creating a cycle. LA routes relax the constraint of being an elementary route in such a manner as to permit efficient pricing. LA routes are best understood in terms of ng-route relaxations. Ng-routes are routes which are permitted to have non-localized cycles in space; this means that at least one intermediate customer (called a breaker) in the cycle must consider the starting customer in the cycle to be spatially far away. LA routes are described using a set of special indexes corresponding to customers on the route ordered from the start to the end of the route. LA route relaxations further restrict the set of permitted cycles beyond that of ng-routes by additionally enforcing that the breaker must be a located at a special index where the set of special indexes is defined recursively as follows. The first special index in the route is at index 1 meaning that it is associated with the first customer in the route. The k'th special index corresponds to the first customer after the k-1'th special index, that is not considered to be a neighbor of (considered spatially far from) the customer located at the k-1'th special index. We demonstrate that LA route relaxations can significantly improve the computational speed of pricing when compared to the standard DSSR.

Multi-Robot Routing with Time Windows: A Column Generation Approach

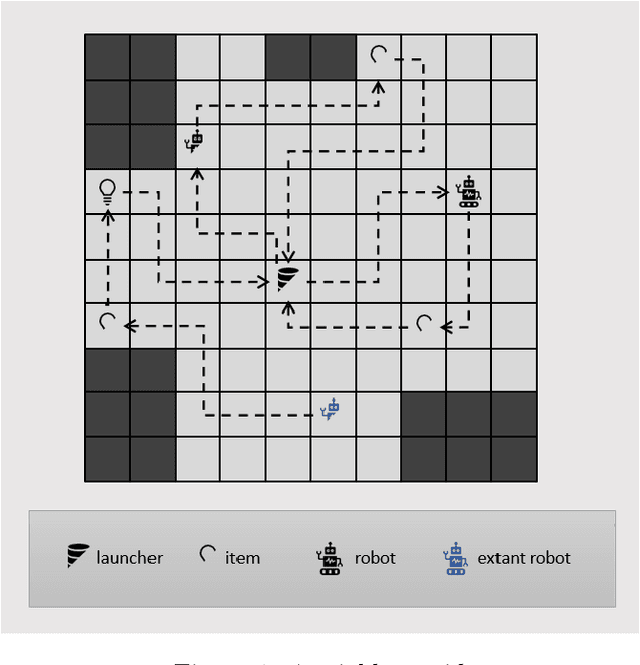
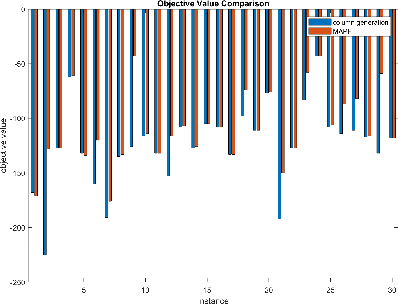
Robots performing tasks in warehouses provide the first example of wide-spread adoption of autonomous vehicles in transportation and logistics. The efficiency of these operations, which can vary widely in practice, are a key factor in the success of supply chains. In this work we consider the problem of coordinating a fleet of robots performing picking operations in a warehouse so as to maximize the net profit achieved within a time period while respecting problem- and robot-specific constraints. We formulate the problem as a weighted set packing problem where the elements in consideration are items on the warehouse floor that can be picked up and delivered within specified time windows. We enforce the constraint that robots must not collide, that each item is picked up and delivered by at most one robot, and that the number of robots active at any time does not exceed the total number available. Since the set of routes is exponential in the size of the input, we attack optimization of the resulting integer linear program using column generation, where pricing amounts to solving an elementary resource-constrained shortest-path problem. We propose an efficient optimization scheme that avoids consideration of every increment within the time windows. We also propose a heuristic pricing algorithm that can efficiently solve the pricing subproblem. While this itself is an important problem, the insights gained from solving these problems effectively can lead to new advances in other time-widow constrained vehicle routing problems.

Integer Programming for Multi-Robot Planning: A Column Generation Approach

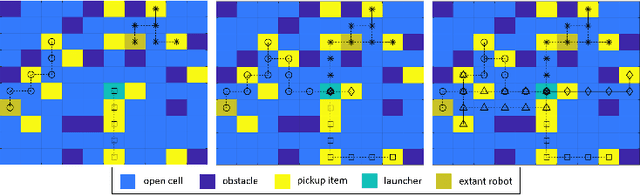
We consider the problem of coordinating a fleet of robots in a warehouse so as to maximize the reward achieved within a time limit while respecting problem and robot specific constraints. We formulate the problem as a weighted set packing problem where elements are defined as being the space-time positions a robot can occupy and the items that can be picked up and delivered. We enforce that robots do not collide, that each item is delivered at most once, and that the number of robots active at any time does not exceed the total number available. Since the set of robot routes is not enumerable, we attack optimization using column generation where pricing is a resource-constrained shortest-path problem.

Relaxed Dual Optimal Inequalities for Relaxed Columns: with Application to Vehicle Routing

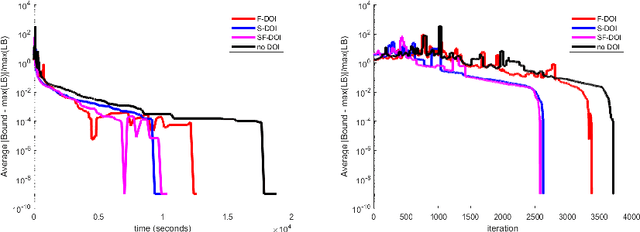
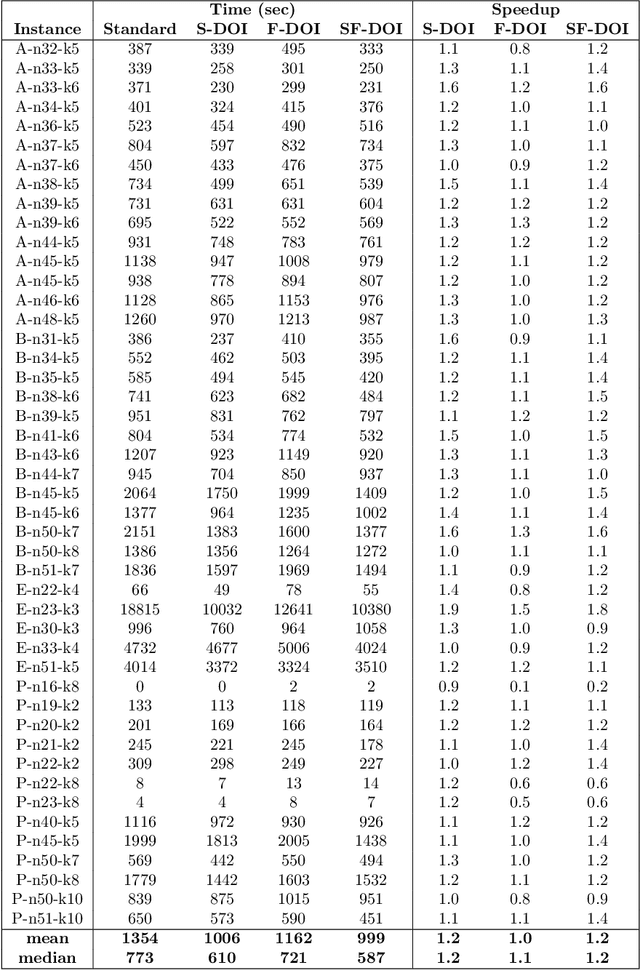
We address the problem of accelerating column generation for set cover problems in which we relax the state space of the columns to do efficient pricing. We achieve this by adapting the recently introduced smooth and flexible dual optimal inequalities (DOI) for use with relaxed columns. Smooth DOI exploit the observation that similar items are nearly fungible, and hence should be associated with similarly valued dual variables. Flexible DOI exploit the observation that the change in cost of a column induced by removing an item can be bounded. We adapt these DOI to the problem of capacitated vehicle routing in the context of ng-route relaxations. We demonstrate significant speed ups on a benchmark data set, while provably not weakening the relaxation.

End-to-end Training of CNN-CRF via Differentiable Dual-Decomposition

Modern computer vision (CV) is often based on convolutional neural networks (CNNs) that excel at hierarchical feature extraction. The previous generation of CV approaches was often based on conditional random fields (CRFs) that excel at modeling flexible higher order interactions. As their benefits are complementary they are often combined. However, these approaches generally use mean-field approximations and thus, arguably, did not directly optimize the real problem. Here we revisit dual-decomposition-based approaches to CRF optimization, an alternative to the mean-field approximation. These algorithms can efficiently and exactly solve sub-problems and directly optimize a convex upper bound of the real problem, providing optimality certificates on the way. Our approach uses a novel fixed-point iteration algorithm which enjoys dual-monotonicity, dual-differentiability and high parallelism. The whole system, CRF and CNN can thus be efficiently trained using back-propagation. We demonstrate the effectiveness of our system on semantic image segmentation, showing consistent improvement over baseline models.

Accelerating Column Generation via Flexible Dual Optimal Inequalities with Application to Entity Resolution

In this paper, we introduce a new optimization approach to Entity Resolution. Traditional approaches tackle entity resolution with hierarchical clustering, which does not benefit from a formal optimization formulation. In contrast, we model entity resolution as correlation-clustering, which we treat as a weighted set-packing problem and write as an integer linear program (ILP). In this case sources in the input data correspond to elements and entities in output data correspond to sets/clusters. We tackle optimization of weighted set packing by relaxing integrality in our ILP formulation. The set of potential sets/clusters can not be explicitly enumerated, thus motivating optimization via column generation. In addition to the novel formulation, we also introduce new dual optimal inequalities (DOI), that we call flexible dual optimal inequalities, which tightly lower-bound dual variables during optimization and accelerate column generation. We apply our formulation to entity resolution (also called de-duplication of records), and achieve state-of-the-art accuracy on two popular benchmark datasets.

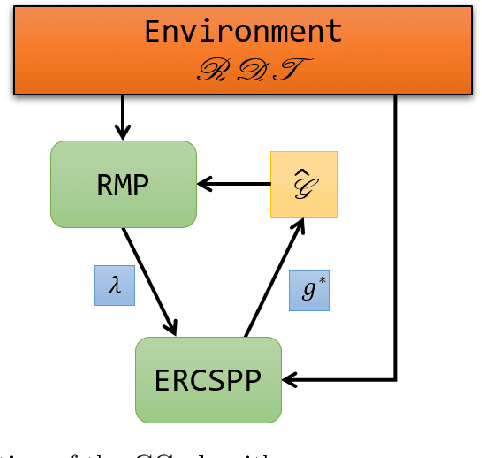
Massively Parallel Benders Decomposition for Correlation Clustering

We tackle the problem of graph partitioning for image segmentation using correlation clustering (CC), which we treat as an integer linear program (ILP). We reformulate optimization in the ILP so as to admit efficient optimization via Benders decomposition, a classic technique from operations research. Our Benders decomposition formulation has many subproblems, each associated with a node in the CC instance's graph, which are solved in parallel. Each Benders subproblem enforces the cycle inequalities corresponding to the negative weight edges attached to its corresponding node in the CC instance. We generate Magnanti-Wong Benders rows in addition to standard Benders rows, to accelerate optimization. Our Benders decomposition approach provides a promising new avenue to accelerate optimization for CC, and allows for massive parallelization.

Accelerating Message Passing for MAP with Benders Decomposition

We introduce a novel mechanism to tighten the local polytope relaxation for MAP inference in Markov random fields with low state space variables. We consider a surjection of the variables to a set of hyper-variables and apply the local polytope relaxation over these hyper-variables. The state space of each individual hyper-variable is constructed to be enumerable while the vector product of pairs is not easily enumerable making message passing inference intractable. To circumvent the difficulty of enumerating the vector product of state spaces of hyper-variables we introduce a novel Benders decomposition approach. This produces an upper envelope describing the message constructed from affine functions of the individual variables that compose the hyper-variable receiving the message. The envelope is tight at the minimizers which are shared by the true message. Benders rows are constructed to be Pareto optimal and are generated using an efficient procedure targeted for binary problems.

Efficient Multi-Person Pose Estimation with Provable Guarantees

Multi-person pose estimation (MPPE) in natural images is key to the meaningful use of visual data in many fields including movement science, security, and rehabilitation. In this paper we tackle MPPE with a bottom-up approach, starting with candidate detections of body parts from a convolutional neural network (CNN) and grouping them into people. We formulate the grouping of body part detections into people as a minimum-weight set packing (MWSP) problem where the set of potential people is the power set of body part detections. We model the quality of a hypothesis of a person which is a set in the MWSP by an augmented tree-structured Markov random field where variables correspond to body-parts and their state-spaces correspond to the power set of the detections for that part. We describe a novel algorithm that combines efficiency with provable bounds on this MWSP problem. We employ an implicit column generation strategy where the pricing problem is formulated as a dynamic program. To efficiently solve this dynamic program we exploit the problem structure utilizing a nested Bender's decomposition (NBD) exact inference strategy which we speed up by recycling Bender's rows between calls to the pricing problem. We test our approach on the MPII-Multiperson dataset, showing that our approach obtains comparable results with the state-of-the-art algorithm for joint node labeling and grouping problems, and that NBD achieves considerable speed-ups relative to a naive dynamic programming approach. Typical algorithms that solve joint node labeling and grouping problems use heuristics and thus can not obtain proofs of optimality. Our approach, in contrast, proves that for over 99 percent of problem instances we find the globally optimal solution and otherwise provide upper/lower bounds.

Efficient Column Generation for Cell Detection and Segmentation

We study the problem of instance segmentation in biological images with crowded and compact cells. We formulate this task as an integer program where variables correspond to cells and constraints enforce that cells do not overlap. To solve this integer program, we propose a column generation formulation where the pricing program is solved via exact optimization of very small scale integer programs. Column generation is tightened using odd set inequalities which fit elegantly into pricing problem optimization. Our column generation approach achieves fast stable anytime inference for our instance segmentation problems. We demonstrate on three distinct light microscopy datasets, with several hundred cells each, that our proposed algorithm rapidly achieves or exceeds state of the art accuracy.