Nothing makes sense in deep learning, except in the light of evolution

Deep Learning (DL) is a surprisingly successful branch of machine learning. The success of DL is usually explained by focusing analysis on a particular recent algorithm and its traits. Instead, we propose that an explanation of the success of DL must look at the population of all algorithms in the field and how they have evolved over time. We argue that cultural evolution is a useful framework to explain the success of DL. In analogy to biology, we use `development' to mean the process converting the pseudocode or text description of an algorithm into a fully trained model. This includes writing the programming code, compiling and running the program, and training the model. If all parts of the process don't align well then the resultant model will be useless (if the code runs at all!). This is a constraint. A core component of evolutionary developmental biology is the concept of deconstraints -- these are modification to the developmental process that avoid complete failure by automatically accommodating changes in other components. We suggest that many important innovations in DL, from neural networks themselves to hyperparameter optimization and AutoGrad, can be seen as developmental deconstraints. These deconstraints can be very helpful to both the particular algorithm in how it handles challenges in implementation and the overall field of DL in how easy it is for new ideas to be generated. We highlight how our perspective can both advance DL and lead to new insights for evolutionary biology.

PDE constraints on smooth hierarchical functions computed by neural networks

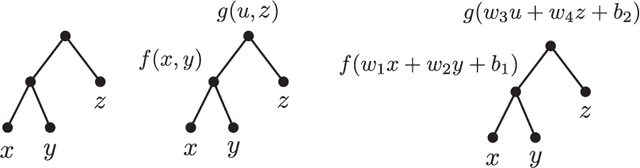
Neural networks are versatile tools for computation, having the ability to approximate a broad range of functions. An important problem in the theory of deep neural networks is expressivity; that is, we want to understand the functions that are computable by a given network. We study real infinitely differentiable (smooth) hierarchical functions implemented by feedforward neural networks via composing simpler functions in two cases: 1) each constituent function of the composition has fewer inputs than the resulting function; 2) constituent functions are in the more specific yet prevalent form of a non-linear univariate function (e.g. tanh) applied to a linear multivariate function. We establish that in each of these regimes there exist non-trivial algebraic partial differential equations (PDEs), which are satisfied by the computed functions. These PDEs are purely in terms of the partial derivatives and are dependent only on the topology of the network. For compositions of polynomial functions, the algebraic PDEs yield non-trivial equations (of degrees dependent only on the architecture) in the ambient polynomial space that are satisfied on the associated functional varieties. Conversely, we conjecture that such PDE constraints, once accompanied by appropriate non-singularity conditions and perhaps certain inequalities involving partial derivatives, guarantee that the smooth function under consideration can be represented by the network. The conjecture is verified in numerous examples including the case of tree architectures which are of neuroscientific interest. Our approach is a step toward formulating an algebraic description of functional spaces associated with specific neural networks, and may provide new, useful tools for constructing neural networks.

Learning to solve the credit assignment problem

Backpropagation is driving today's artificial neural networks (ANNs). However, despite extensive research, it remains unclear if the brain implements this algorithm. Among neuroscientists, reinforcement learning (RL) algorithms are often seen as a realistic alternative: neurons can randomly introduce change, and use unspecific feedback signals to observe their effect on the cost and thus approximate their gradient. However, the convergence rate of such learning scales poorly with the number of involved neurons (e.g. O(N)). Here we propose a hybrid learning approach. Each neuron uses an RL-type strategy to learn how to approximate the gradients that backpropagation would provide -- in this way it learns to learn. We provide proof that our approach converges to the true gradient for certain classes of networks. In both feed-forward and recurrent networks, we empirically show that our approach learns to approximate the gradient, and can match the performance of gradient-based learning. Learning to learn provides a biologically plausible mechanism of achieving good performance, without the need for precise, pre-specified learning rules.

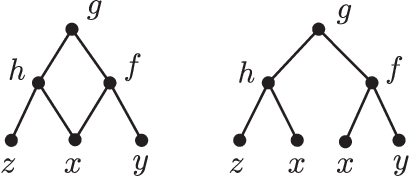
On functions computed on trees

Any function can be constructed using a hierarchy of simpler functions through compositions. Such a hierarchy can be characterized by a binary rooted tree. Each node of this tree is associated with a function which takes as inputs two numbers from its children and produces one output. Since thinking about functions in terms of computation graphs is getting popular we may want to know which functions can be implemented on a given tree. Here, we describe a set of necessary constraints in the form of a system of non-linear partial differential equations that must be satisfied. Moreover, we prove that these conditions are sufficient in both contexts of analytic and bit-value functions. In the latter case, we explicitly enumerate discrete functions and observe that there are relatively few. Our point of view allows us to compare different neural network architectures in regard to their function spaces. Our work connects the structure of computation graphs with the functions they can implement and has potential applications to neuroscience and computer science.

Towards learning-to-learn

In good old-fashioned artificial intelligence (GOFAI), humans specified systems that solved problems. Much of the recent progress in AI has come from replacing human insights by learning. However, learning itself is still usually built by humans -- specifically the choice that parameter updates should follow the gradient of a cost function. Yet, in analogy with GOFAI, there is no reason to believe that humans are particularly good at defining such learning systems: we may expect learning itself to be better if we learn it. Recent research in machine learning has started to realize the benefits of that strategy. We should thus expect this to be relevant for neuroscience: how could the correct learning rules be acquired? Indeed, behavioral science has long shown that humans learn-to-learn, which is potentially responsible for their impressive learning abilities. Here we discuss ideas across machine learning, neuroscience, and behavioral science that matter for the principle of learning-to-learn.

Efficient Multi-Person Pose Estimation with Provable Guarantees

Multi-person pose estimation (MPPE) in natural images is key to the meaningful use of visual data in many fields including movement science, security, and rehabilitation. In this paper we tackle MPPE with a bottom-up approach, starting with candidate detections of body parts from a convolutional neural network (CNN) and grouping them into people. We formulate the grouping of body part detections into people as a minimum-weight set packing (MWSP) problem where the set of potential people is the power set of body part detections. We model the quality of a hypothesis of a person which is a set in the MWSP by an augmented tree-structured Markov random field where variables correspond to body-parts and their state-spaces correspond to the power set of the detections for that part. We describe a novel algorithm that combines efficiency with provable bounds on this MWSP problem. We employ an implicit column generation strategy where the pricing problem is formulated as a dynamic program. To efficiently solve this dynamic program we exploit the problem structure utilizing a nested Bender's decomposition (NBD) exact inference strategy which we speed up by recycling Bender's rows between calls to the pricing problem. We test our approach on the MPII-Multiperson dataset, showing that our approach obtains comparable results with the state-of-the-art algorithm for joint node labeling and grouping problems, and that NBD achieves considerable speed-ups relative to a naive dynamic programming approach. Typical algorithms that solve joint node labeling and grouping problems use heuristics and thus can not obtain proofs of optimality. Our approach, in contrast, proves that for over 99 percent of problem instances we find the globally optimal solution and otherwise provide upper/lower bounds.