PDE constraints on smooth hierarchical functions computed by neural networks

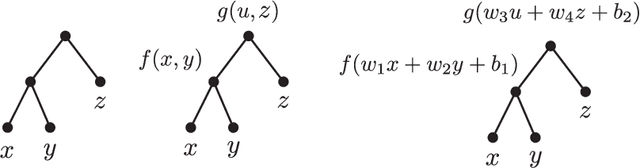
Neural networks are versatile tools for computation, having the ability to approximate a broad range of functions. An important problem in the theory of deep neural networks is expressivity; that is, we want to understand the functions that are computable by a given network. We study real infinitely differentiable (smooth) hierarchical functions implemented by feedforward neural networks via composing simpler functions in two cases: 1) each constituent function of the composition has fewer inputs than the resulting function; 2) constituent functions are in the more specific yet prevalent form of a non-linear univariate function (e.g. tanh) applied to a linear multivariate function. We establish that in each of these regimes there exist non-trivial algebraic partial differential equations (PDEs), which are satisfied by the computed functions. These PDEs are purely in terms of the partial derivatives and are dependent only on the topology of the network. For compositions of polynomial functions, the algebraic PDEs yield non-trivial equations (of degrees dependent only on the architecture) in the ambient polynomial space that are satisfied on the associated functional varieties. Conversely, we conjecture that such PDE constraints, once accompanied by appropriate non-singularity conditions and perhaps certain inequalities involving partial derivatives, guarantee that the smooth function under consideration can be represented by the network. The conjecture is verified in numerous examples including the case of tree architectures which are of neuroscientific interest. Our approach is a step toward formulating an algebraic description of functional spaces associated with specific neural networks, and may provide new, useful tools for constructing neural networks.

On functions computed on trees

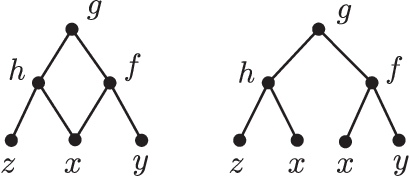
Any function can be constructed using a hierarchy of simpler functions through compositions. Such a hierarchy can be characterized by a binary rooted tree. Each node of this tree is associated with a function which takes as inputs two numbers from its children and produces one output. Since thinking about functions in terms of computation graphs is getting popular we may want to know which functions can be implemented on a given tree. Here, we describe a set of necessary constraints in the form of a system of non-linear partial differential equations that must be satisfied. Moreover, we prove that these conditions are sufficient in both contexts of analytic and bit-value functions. In the latter case, we explicitly enumerate discrete functions and observe that there are relatively few. Our point of view allows us to compare different neural network architectures in regard to their function spaces. Our work connects the structure of computation graphs with the functions they can implement and has potential applications to neuroscience and computer science.

The Roles of Supervised Machine Learning in Systems Neuroscience

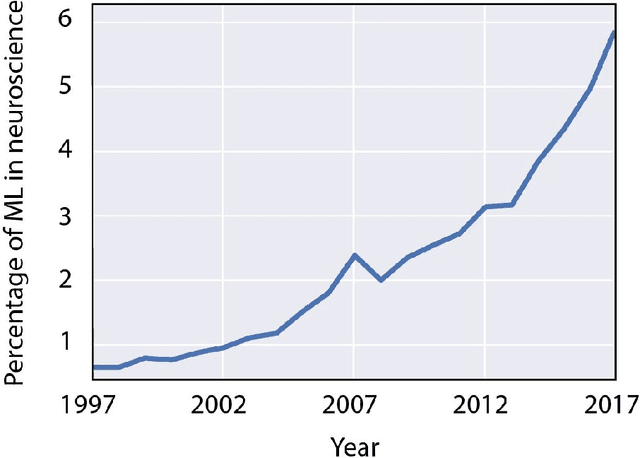
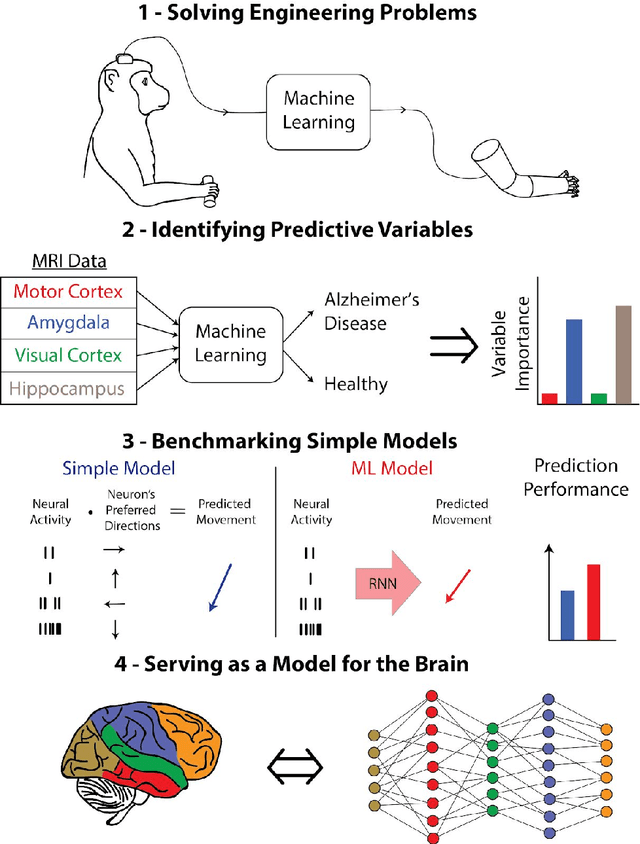
Over the last several years, the use of machine learning (ML) in neuroscience has been increasing exponentially. Here, we review ML's contributions, both realized and potential, across several areas of systems neuroscience. We describe four primary roles of ML within neuroscience: 1) creating solutions to engineering problems, 2) identifying predictive variables, 3) setting benchmarks for simple models of the brain, and 4) serving itself as a model for the brain. The breadth and ease of its applicability suggests that machine learning should be in the toolbox of most systems neuroscientists.