MBExplainer: Multilevel bandit-based explanations for downstream models with augmented graph embeddings

In many industrial applications, it is common that the graph embeddings generated from training GNNs are used in an ensemble model where the embeddings are combined with other tabular features (e.g., original node or edge features) in a downstream ML task. The tabular features may even arise naturally if, e.g., one tries to build a graph such that some of the node or edge features are stored in a tabular format. Here we address the problem of explaining the output of such ensemble models for which the input features consist of learned neural graph embeddings combined with additional tabular features. We propose MBExplainer, a model-agnostic explanation approach for downstream models with augmented graph embeddings. MBExplainer returns a human-legible triple as an explanation for an instance prediction of the whole pipeline consisting of three components: a subgraph with the highest importance, the topmost important nodal features, and the topmost important augmented downstream features. A game-theoretic formulation is used to take the contributions of each component and their interactions into account by assigning three Shapley values corresponding to their own specific games. Finding the explanation requires an efficient search through the corresponding local search spaces corresponding to each component. MBExplainer applies a novel multilevel search algorithm that enables simultaneous pruning of local search spaces in a computationally tractable way. In particular, three interweaved Monte Carlo Tree Search are utilized to iteratively prune the local search spaces. MBExplainer also includes a global search algorithm that uses contextual bandits to efficiently allocate pruning budget among the local search spaces. We show the effectiveness of MBExplainer by presenting a set of comprehensive numerical examples on multiple public graph datasets for both node and graph classification tasks.

Mechanistic interpretability of large language models with applications to the financial services industry

Large Language Models such as GPTs (Generative Pre-trained Transformers) exhibit remarkable capabilities across a broad spectrum of applications. Nevertheless, due to their intrinsic complexity, these models present substantial challenges in interpreting their internal decision-making processes. This lack of transparency poses critical challenges when it comes to their adaptation by financial institutions, where concerns and accountability regarding bias, fairness, and reliability are of paramount importance. Mechanistic interpretability aims at reverse engineering complex AI models such as transformers. In this paper, we are pioneering the use of mechanistic interpretability to shed some light on the inner workings of large language models for use in financial services applications. We offer several examples of how algorithmic tasks can be designed for compliance monitoring purposes. In particular, we investigate GPT-2 Small's attention pattern when prompted to identify potential violation of Fair Lending laws. Using direct logit attribution, we study the contributions of each layer and its corresponding attention heads to the logit difference in the residual stream. Finally, we design clean and corrupted prompts and use activation patching as a causal intervention method to localize our task completion components further. We observe that the (positive) heads $10.2$ (head $2$, layer $10$), $10.7$, and $11.3$, as well as the (negative) heads $9.6$ and $10.6$ play a significant role in the task completion.

Approximation of group explainers with coalition structure using Monte Carlo sampling on the product space of coalitions and features

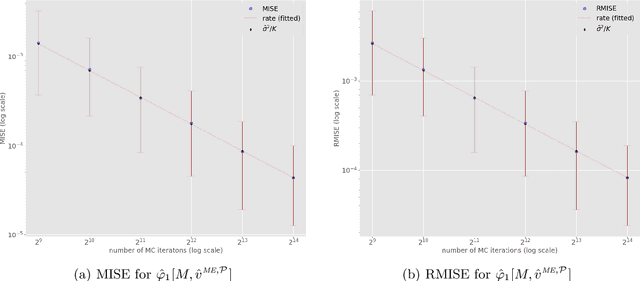
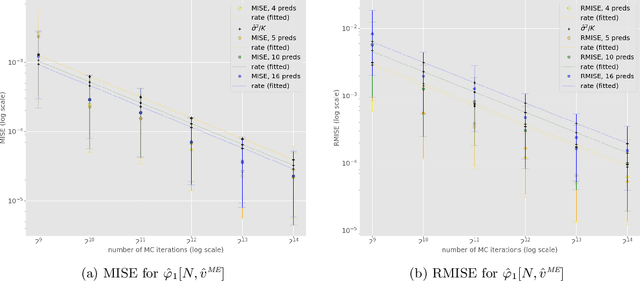
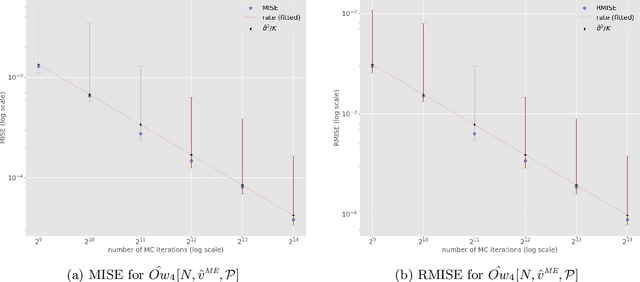
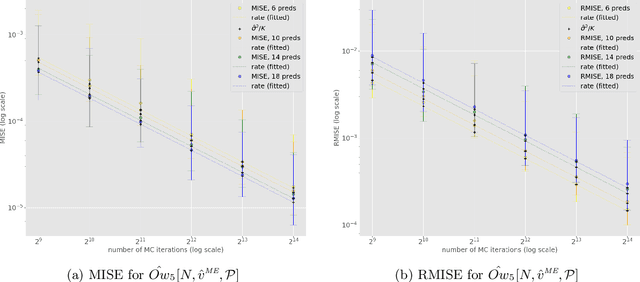
In recent years, many Machine Learning (ML) explanation techniques have been designed using ideas from cooperative game theory. These game-theoretic explainers suffer from high complexity, hindering their exact computation in practical settings. In our work, we focus on a wide class of linear game values, as well as coalitional values, for the marginal game based on a given ML model and predictor vector. By viewing these explainers as expectations over appropriate sample spaces, we design a novel Monte Carlo sampling algorithm that estimates them at a reduced complexity that depends linearly on the size of the background dataset. We set up a rigorous framework for the statistical analysis and obtain error bounds for our sampling methods. The advantage of this approach is that it is fast, easily implementable, and model-agnostic. Furthermore, it has similar statistical accuracy as other known estimation techniques that are more complex and model-specific. We provide rigorous proofs of statistical convergence, as well as numerical experiments whose results agree with our theoretical findings.

On marginal feature attributions of tree-based models

Due to their power and ease of use, tree-based machine learning models have become very popular. To interpret these models, local feature attributions based on marginal expectations e.g. marginal (interventional) Shapley, Owen or Banzhaf values may be employed. Such feature attribution methods are true to the model and implementation invariant, i.e. dependent only on the input-output function of the model. By taking advantage of the internal structure of tree-based models, we prove that their marginal Shapley values, or more generally marginal feature attributions obtained from a linear game value, are simple (piecewise-constant) functions with respect to a certain finite partition of the input space determined by the trained model. The same is true for feature attributions obtained from the famous TreeSHAP algorithm. Nevertheless, we show that the "path-dependent" TreeSHAP is not implementation invariant by presenting two (statistically similar) decision trees computing the exact same function for which the algorithm yields different rankings of features, whereas the marginal Shapley values coincide. Furthermore, we discuss how the fact that marginal feature attributions are simple functions can potentially be utilized to compute them. An important observation, showcased by experiments with XGBoost, LightGBM and CatBoost libraries, is that only a portion of all features appears in a tree from the ensemble; thus the complexity of computing marginal Shapley (or Owen or Banzhaf) feature attributions may be reduced. In particular, in the case of CatBoost models, the trees are oblivious (symmetric) and the number of features in each of them is no larger than the depth. We exploit the symmetry to derive an explicit formula with improved complexity for marginal Shapley (and Banzhaf and Owen) values which is only in terms of the internal parameters of the CatBoost model.

PDE constraints on smooth hierarchical functions computed by neural networks

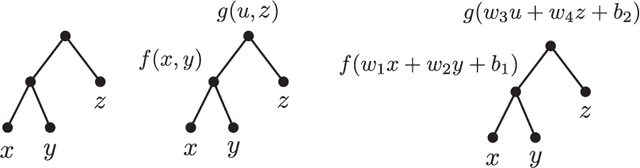
Neural networks are versatile tools for computation, having the ability to approximate a broad range of functions. An important problem in the theory of deep neural networks is expressivity; that is, we want to understand the functions that are computable by a given network. We study real infinitely differentiable (smooth) hierarchical functions implemented by feedforward neural networks via composing simpler functions in two cases: 1) each constituent function of the composition has fewer inputs than the resulting function; 2) constituent functions are in the more specific yet prevalent form of a non-linear univariate function (e.g. tanh) applied to a linear multivariate function. We establish that in each of these regimes there exist non-trivial algebraic partial differential equations (PDEs), which are satisfied by the computed functions. These PDEs are purely in terms of the partial derivatives and are dependent only on the topology of the network. For compositions of polynomial functions, the algebraic PDEs yield non-trivial equations (of degrees dependent only on the architecture) in the ambient polynomial space that are satisfied on the associated functional varieties. Conversely, we conjecture that such PDE constraints, once accompanied by appropriate non-singularity conditions and perhaps certain inequalities involving partial derivatives, guarantee that the smooth function under consideration can be represented by the network. The conjecture is verified in numerous examples including the case of tree architectures which are of neuroscientific interest. Our approach is a step toward formulating an algebraic description of functional spaces associated with specific neural networks, and may provide new, useful tools for constructing neural networks.

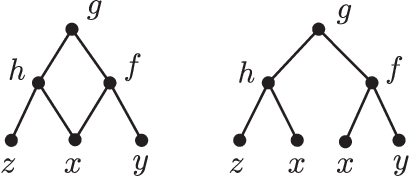
On functions computed on trees

Any function can be constructed using a hierarchy of simpler functions through compositions. Such a hierarchy can be characterized by a binary rooted tree. Each node of this tree is associated with a function which takes as inputs two numbers from its children and produces one output. Since thinking about functions in terms of computation graphs is getting popular we may want to know which functions can be implemented on a given tree. Here, we describe a set of necessary constraints in the form of a system of non-linear partial differential equations that must be satisfied. Moreover, we prove that these conditions are sufficient in both contexts of analytic and bit-value functions. In the latter case, we explicitly enumerate discrete functions and observe that there are relatively few. Our point of view allows us to compare different neural network architectures in regard to their function spaces. Our work connects the structure of computation graphs with the functions they can implement and has potential applications to neuroscience and computer science.