Approximation of group explainers with coalition structure using Monte Carlo sampling on the product space of coalitions and features

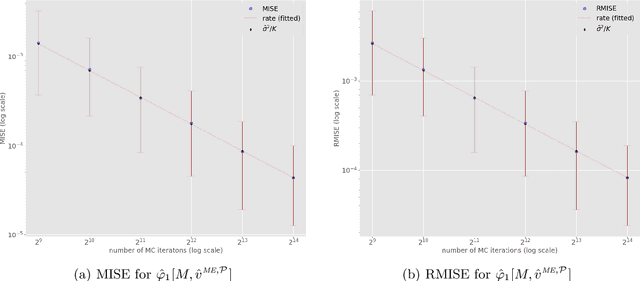
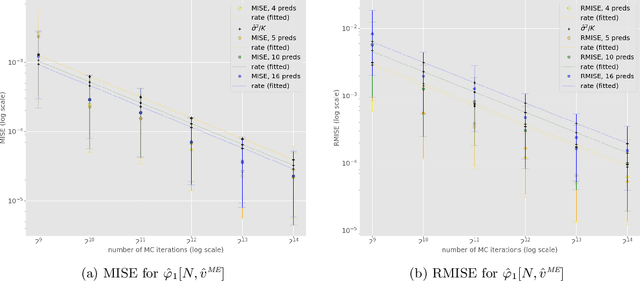
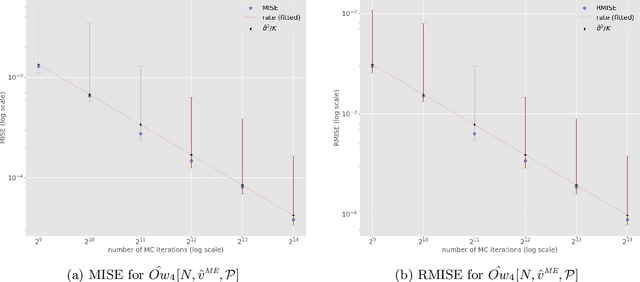
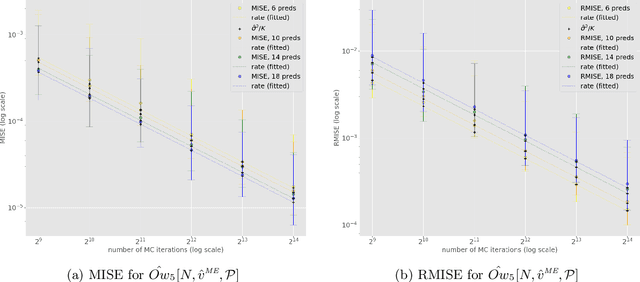
In recent years, many Machine Learning (ML) explanation techniques have been designed using ideas from cooperative game theory. These game-theoretic explainers suffer from high complexity, hindering their exact computation in practical settings. In our work, we focus on a wide class of linear game values, as well as coalitional values, for the marginal game based on a given ML model and predictor vector. By viewing these explainers as expectations over appropriate sample spaces, we design a novel Monte Carlo sampling algorithm that estimates them at a reduced complexity that depends linearly on the size of the background dataset. We set up a rigorous framework for the statistical analysis and obtain error bounds for our sampling methods. The advantage of this approach is that it is fast, easily implementable, and model-agnostic. Furthermore, it has similar statistical accuracy as other known estimation techniques that are more complex and model-specific. We provide rigorous proofs of statistical convergence, as well as numerical experiments whose results agree with our theoretical findings.

On marginal feature attributions of tree-based models

Due to their power and ease of use, tree-based machine learning models have become very popular. To interpret these models, local feature attributions based on marginal expectations e.g. marginal (interventional) Shapley, Owen or Banzhaf values may be employed. Such feature attribution methods are true to the model and implementation invariant, i.e. dependent only on the input-output function of the model. By taking advantage of the internal structure of tree-based models, we prove that their marginal Shapley values, or more generally marginal feature attributions obtained from a linear game value, are simple (piecewise-constant) functions with respect to a certain finite partition of the input space determined by the trained model. The same is true for feature attributions obtained from the famous TreeSHAP algorithm. Nevertheless, we show that the "path-dependent" TreeSHAP is not implementation invariant by presenting two (statistically similar) decision trees computing the exact same function for which the algorithm yields different rankings of features, whereas the marginal Shapley values coincide. Furthermore, we discuss how the fact that marginal feature attributions are simple functions can potentially be utilized to compute them. An important observation, showcased by experiments with XGBoost, LightGBM and CatBoost libraries, is that only a portion of all features appears in a tree from the ensemble; thus the complexity of computing marginal Shapley (or Owen or Banzhaf) feature attributions may be reduced. In particular, in the case of CatBoost models, the trees are oblivious (symmetric) and the number of features in each of them is no larger than the depth. We exploit the symmetry to derive an explicit formula with improved complexity for marginal Shapley (and Banzhaf and Owen) values which is only in terms of the internal parameters of the CatBoost model.

Model-agnostic bias mitigation methods with regressor distribution control for Wasserstein-based fairness metrics

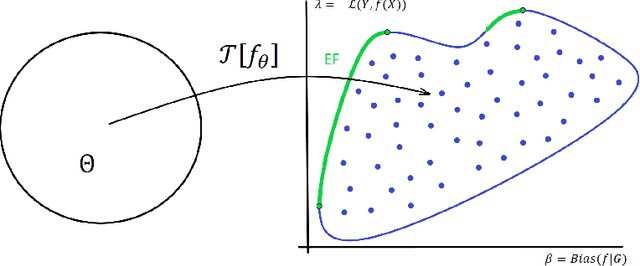
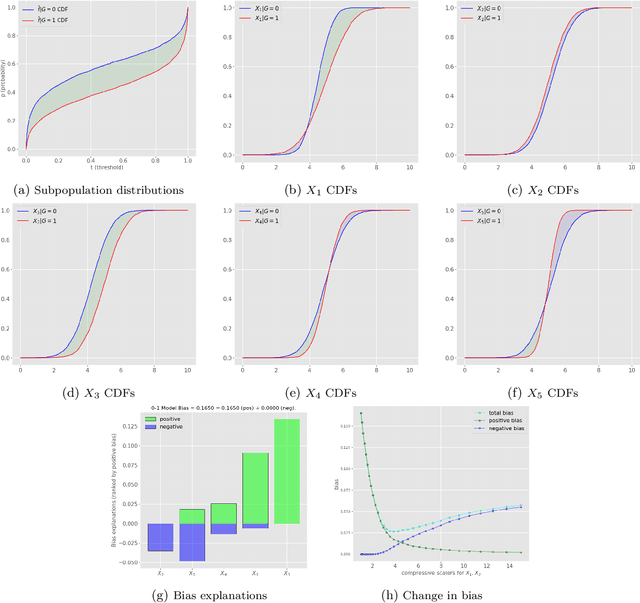
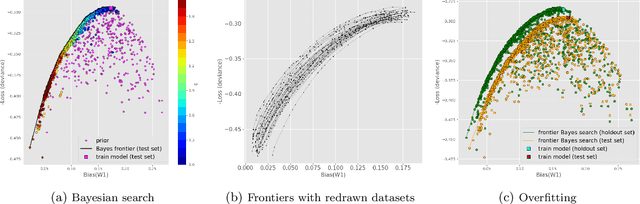
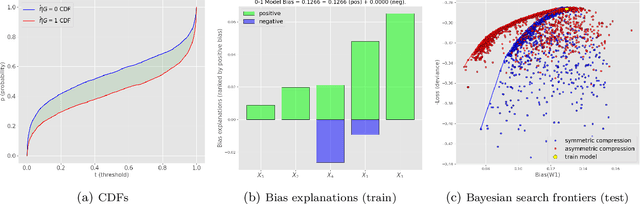
This article is a companion paper to our earlier work Miroshnikov et al. (2021) on fairness interpretability, which introduces bias explanations. In the current work, we propose a bias mitigation methodology based upon the construction of post-processed models with fairer regressor distributions for Wasserstein-based fairness metrics. By identifying the list of predictors contributing the most to the bias, we reduce the dimensionality of the problem by mitigating the bias originating from those predictors. The post-processing methodology involves reshaping the predictor distributions by balancing the positive and negative bias explanations and allows for the regressor bias to decrease. We design an algorithm that uses Bayesian optimization to construct the bias-performance efficient frontier over the family of post-processed models, from which an optimal model is selected. Our novel methodology performs optimization in low-dimensional spaces and avoids expensive model retraining.

Wasserstein-based fairness interpretability framework for machine learning models

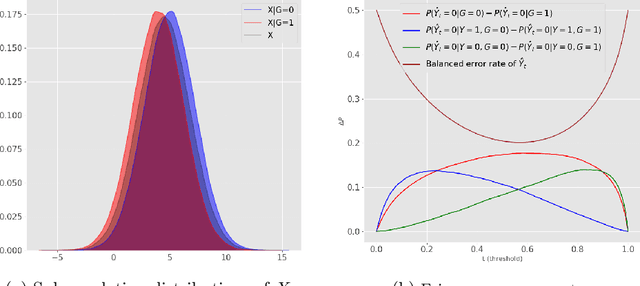
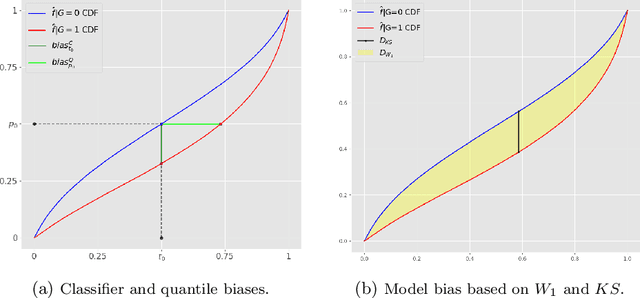
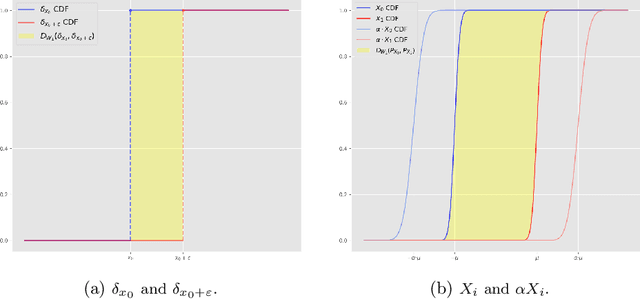
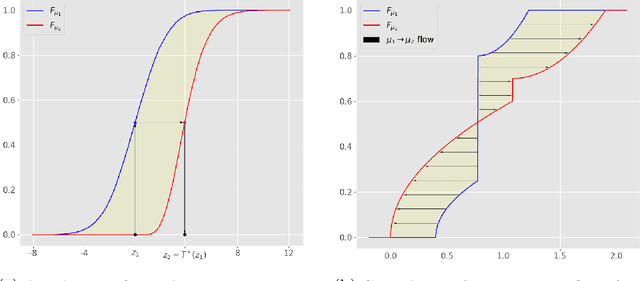
In this article, we introduce a fairness interpretability framework for measuring and explaining bias in classification and regression models at the level of a distribution. In our work, motivated by the ideas of Dwork et al. (2012), we measure the model bias across sub-population distributions using the Wasserstein metric. The transport theory characterization of the Wasserstein metric allows us to take into account the sign of the bias across the model distribution which in turn yields the decomposition of the model bias into positive and negative components. To understand how predictors contribute to the model bias, we introduce and theoretically characterize bias predictor attributions called bias explanations. We also provide the formulation for the bias explanations that take into account the impact of missing values. In addition, motivated by the works of Strumbelj and Kononenko (2014) and Lundberg and Lee (2017) we construct additive bias explanations by employing cooperative game theory.