Walking the Weight Manifold: a Topological Approach to Conditioning Inspired by Neuromodulation

One frequently wishes to learn a range of similar tasks as efficiently as possible, re-using knowledge across tasks. In artificial neural networks, this is typically accomplished by conditioning a network upon task context by injecting context as input. Brains have a different strategy: the parameters themselves are modulated as a function of various neuromodulators such as serotonin. Here, we take inspiration from neuromodulation and propose to learn weights which are smoothly parameterized functions of task context variables. Rather than optimize a weight vector, i.e. a single point in weight space, we optimize a smooth manifold in weight space with a predefined topology. To accomplish this, we derive a formal treatment of optimization of manifolds as the minimization of a loss functional subject to a constraint on volumetric movement, analogous to gradient descent. During inference, conditioning selects a single point on this manifold which serves as the effective weight matrix for a particular sub-task. This strategy for conditioning has two main advantages. First, the topology of the manifold (whether a line, circle, or torus) is a convenient lever for inductive biases about the relationship between tasks. Second, learning in one state smoothly affects the entire manifold, encouraging generalization across states. To verify this, we train manifolds with several topologies, including straight lines in weight space (for conditioning on e.g. noise level in input data) and ellipses (for rotated images). Despite their simplicity, these parameterizations outperform conditioning identical networks by input concatenation and better generalize to out-of-distribution samples. These results suggest that modulating weights over low-dimensional manifolds offers a principled and effective alternative to traditional conditioning.

Token-Level Uncertainty-Aware Objective for Language Model Post-Training

In the current work, we connect token-level uncertainty in causal language modeling to two types of training objectives: 1) masked maximum likelihood (MLE), 2) self-distillation. We show that masked MLE is effective in reducing epistemic uncertainty, and serve as an effective token-level automatic curriculum learning technique. However, masked MLE is prone to overfitting and requires self-distillation regularization to improve or maintain performance on out-of-distribution tasks. We demonstrate significant performance gain via the proposed training objective - combined masked MLE and self-distillation - across multiple architectures (Gemma, LLaMA, Phi) and datasets (Alpaca, ShareGPT, GSM8K), mitigating overfitting while maintaining adaptability during post-training. Our findings suggest that uncertainty-aware training provides an effective mechanism for enhancing language model training.

Continual learning with the neural tangent ensemble

A natural strategy for continual learning is to weigh a Bayesian ensemble of fixed functions. This suggests that if a (single) neural network could be interpreted as an ensemble, one could design effective algorithms that learn without forgetting. To realize this possibility, we observe that a neural network classifier with N parameters can be interpreted as a weighted ensemble of N classifiers, and that in the lazy regime limit these classifiers are fixed throughout learning. We term these classifiers the neural tangent experts and show they output valid probability distributions over the labels. We then derive the likelihood and posterior probability of each expert given past data. Surprisingly, we learn that the posterior updates for these experts are equivalent to a scaled and projected form of stochastic gradient descent (SGD) over the network weights. Away from the lazy regime, networks can be seen as ensembles of adaptive experts which improve over time. These results offer a new interpretation of neural networks as Bayesian ensembles of experts, providing a principled framework for understanding and mitigating catastrophic forgetting in continual learning settings.

Object Based Attention Through Internal Gating

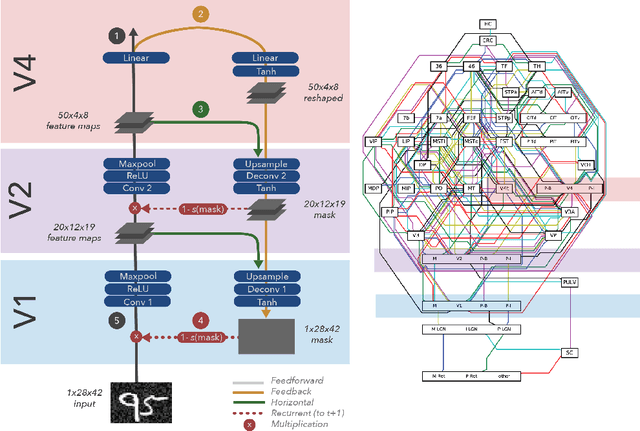
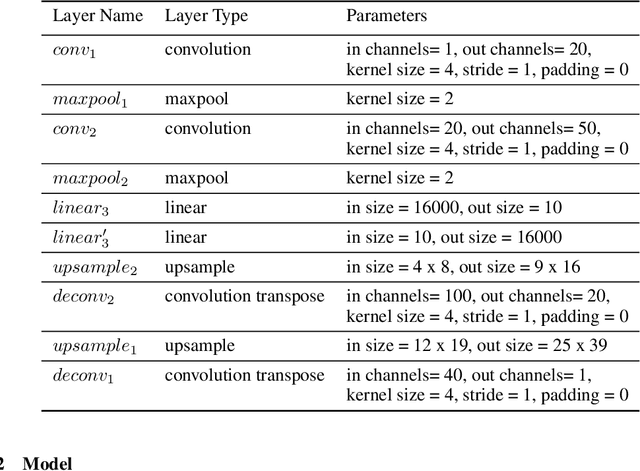
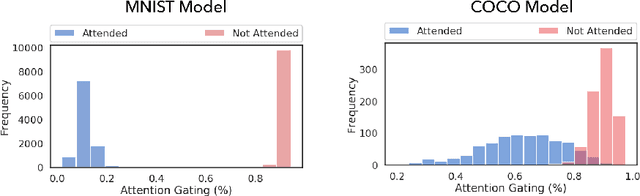
Object-based attention is a key component of the visual system, relevant for perception, learning, and memory. Neurons tuned to features of attended objects tend to be more active than those associated with non-attended objects. There is a rich set of models of this phenomenon in computational neuroscience. However, there is currently a divide between models that successfully match physiological data but can only deal with extremely simple problems and models of attention used in computer vision. For example, attention in the brain is known to depend on top-down processing, whereas self-attention in deep learning does not. Here, we propose an artificial neural network model of object-based attention that captures the way in which attention is both top-down and recurrent. Our attention model works well both on simple test stimuli, such as those using images of handwritten digits, and on more complex stimuli, such as natural images drawn from the COCO dataset. We find that our model replicates a range of findings from neuroscience, including attention-invariant tuning, inhibition of return, and attention-mediated scaling of activity. Understanding object based attention is both computationally interesting and a key problem for computational neuroscience.

An adversarial algorithm for variational inference with a new role for acetylcholine

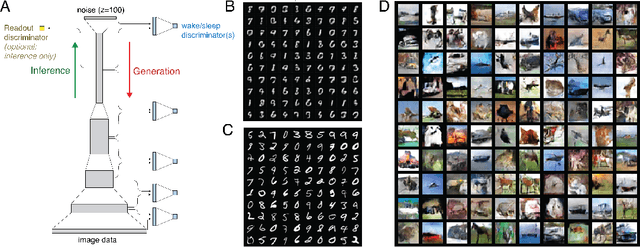
Sensory learning in the mammalian cortex has long been hypothesized to involve the objective of variational inference (VI). Likely the most well-known algorithm for cortical VI is the Wake-Sleep algorithm (Hinton et al. 1995). However Wake-Sleep problematically assumes that neural activities are independent given lower-layers during generation. Here, we construct a VI system that is both compatible with neurobiology and avoids this assumption. The core of the system is a wake-sleep discriminator that classifies network states as inferred or self-generated. Inference connections learn by opposing this discriminator. This adversarial dynamic solves a core problem within VI, which is to match the distribution of stimulus-evoked (inference) activity to that of self-generated activity. Meanwhile, generative connections learn to predict lower-level activity as in standard VI. We implement this algorithm and show that it can successfully train the approximate inference network for generative models. Our proposed algorithm makes several biological predictions that can be tested. Most importantly, it predicts a teaching signal that is remarkably similar to known properties of the cholinergic system.

Measuring and regularizing networks in function space

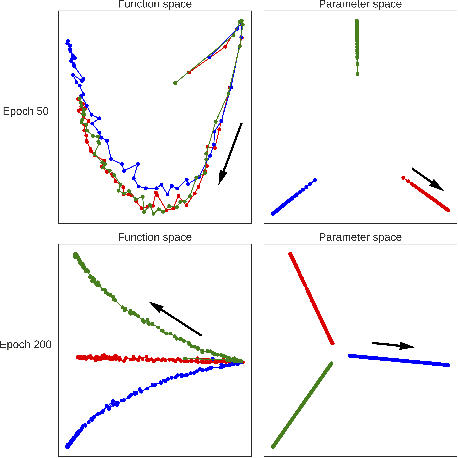
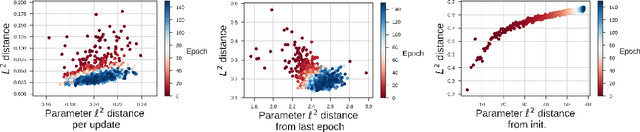
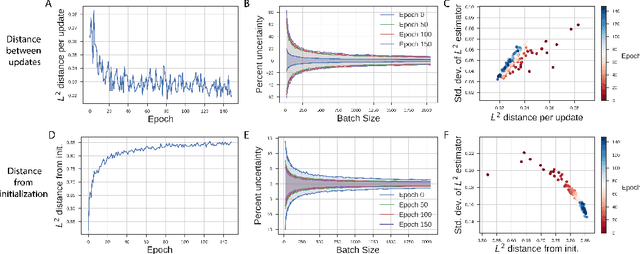
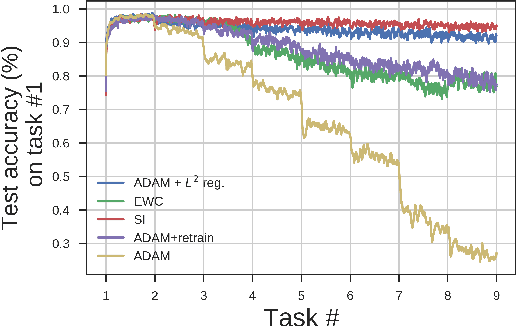
Neural network optimization is often conceptualized as optimizing parameters, but it is ultimately a matter of optimizing a function defined by inputs and outputs. However, little work has empirically evaluated network optimization in the space of possible functions and much analysis relies on Lipschitz bounds. Here, we measure the behavior of several networks in an $L^2$ Hilbert space. Lipschitz bounds appear reasonable in late optimization but not the beginning. We also observe that the function continues to change even after test error saturates. In light of this we propose a learning rule, Hilbert-constrained gradient descent (HCGD), that regularizes the distance a network can travel through $L^2$-space in any one update. HCGD should increase generalization if it is important that single updates minimally change the output function. Experiments show that HCGD reduces exploration in function space and often, but not always, improves generalization. We connect this idea to the natural gradient, which can also be derived from penalizing changes in the outputs. We conclude that decreased movement in function space is an important consideration in training neural networks.

The Roles of Supervised Machine Learning in Systems Neuroscience

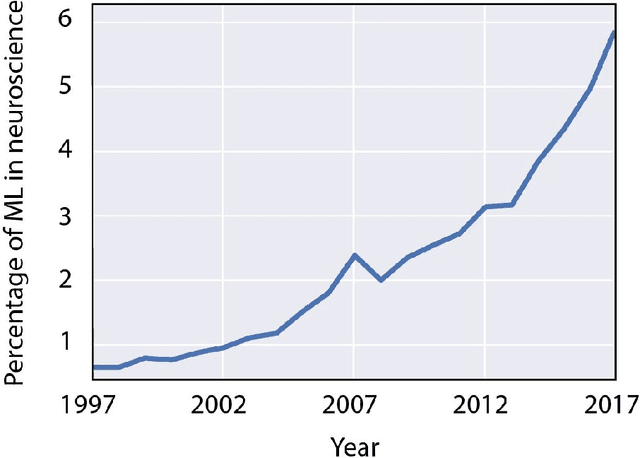
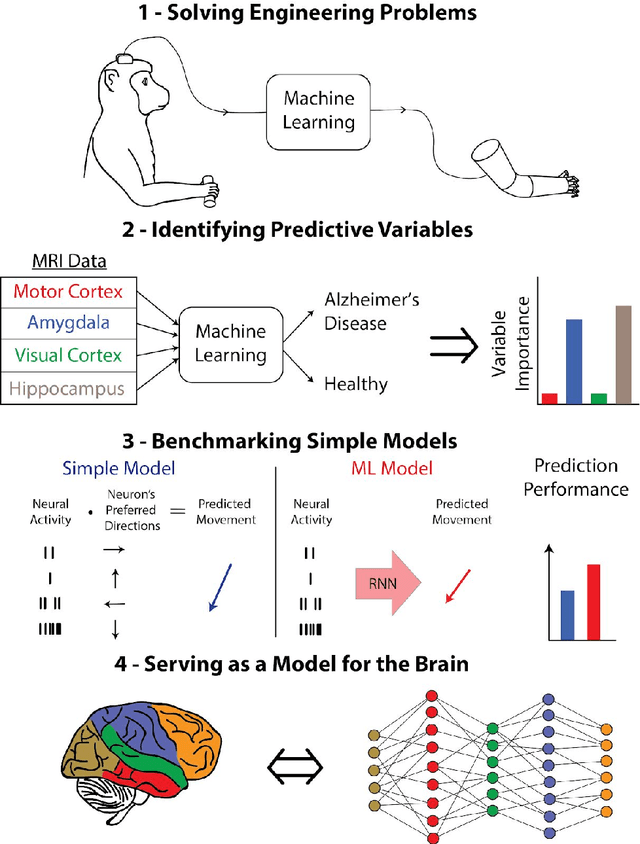
Over the last several years, the use of machine learning (ML) in neuroscience has been increasing exponentially. Here, we review ML's contributions, both realized and potential, across several areas of systems neuroscience. We describe four primary roles of ML within neuroscience: 1) creating solutions to engineering problems, 2) identifying predictive variables, 3) setting benchmarks for simple models of the brain, and 4) serving itself as a model for the brain. The breadth and ease of its applicability suggests that machine learning should be in the toolbox of most systems neuroscientists.