Continual learning with the neural tangent ensemble

A natural strategy for continual learning is to weigh a Bayesian ensemble of fixed functions. This suggests that if a (single) neural network could be interpreted as an ensemble, one could design effective algorithms that learn without forgetting. To realize this possibility, we observe that a neural network classifier with N parameters can be interpreted as a weighted ensemble of N classifiers, and that in the lazy regime limit these classifiers are fixed throughout learning. We term these classifiers the neural tangent experts and show they output valid probability distributions over the labels. We then derive the likelihood and posterior probability of each expert given past data. Surprisingly, we learn that the posterior updates for these experts are equivalent to a scaled and projected form of stochastic gradient descent (SGD) over the network weights. Away from the lazy regime, networks can be seen as ensembles of adaptive experts which improve over time. These results offer a new interpretation of neural networks as Bayesian ensembles of experts, providing a principled framework for understanding and mitigating catastrophic forgetting in continual learning settings.

Information Bottleneck-Based Hebbian Learning Rule Naturally Ties Working Memory and Synaptic Updates

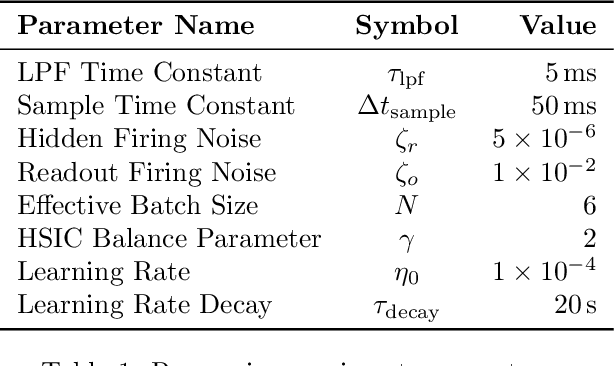
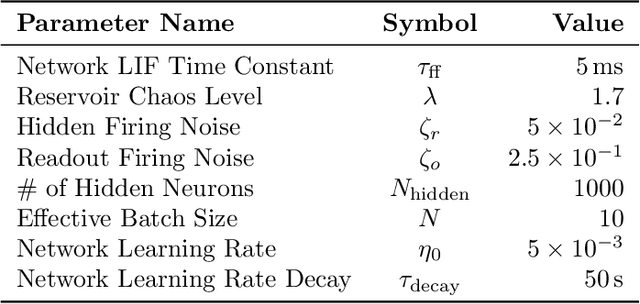
Artificial neural networks have successfully tackled a large variety of problems by training extremely deep networks via back-propagation. A direct application of back-propagation to spiking neural networks contains biologically implausible components, like the weight transport problem or separate inference and learning phases. Various methods address different components individually, but a complete solution remains intangible. Here, we take an alternate approach that avoids back-propagation and its associated issues entirely. Recent work in deep learning proposed independently training each layer of a network via the information bottleneck (IB). Subsequent studies noted that this layer-wise approach circumvents error propagation across layers, leading to a biologically plausible paradigm. Unfortunately, the IB is computed using a batch of samples. The prior work addresses this with a weight update that only uses two samples (the current and previous sample). Our work takes a different approach by decomposing the weight update into a local and global component. The local component is Hebbian and only depends on the current sample. The global component computes a layer-wise modulatory signal that depends on a batch of samples. We show that this modulatory signal can be learned by an auxiliary circuit with working memory (WM) like a reservoir. Thus, we can use batch sizes greater than two, and the batch size determines the required capacity of the WM. To the best of our knowledge, our rule is the first biologically plausible mechanism to directly couple synaptic updates with a WM of the task. We evaluate our rule on synthetic datasets and image classification datasets like MNIST, and we explore the effect of the WM capacity on learning performance. We hope our work is a first-step towards understanding the mechanistic role of memory in learning.

Accelerating Deep Learning with Dynamic Data Pruning

Deep learning's success has been attributed to the training of large, overparameterized models on massive amounts of data. As this trend continues, model training has become prohibitively costly, requiring access to powerful computing systems to train state-of-the-art networks. A large body of research has been devoted to addressing the cost per iteration of training through various model compression techniques like pruning and quantization. Less effort has been spent targeting the number of iterations. Previous work, such as forget scores and GraNd/EL2N scores, address this problem by identifying important samples within a full dataset and pruning the remaining samples, thereby reducing the iterations per epoch. Though these methods decrease the training time, they use expensive static scoring algorithms prior to training. When accounting for the scoring mechanism, the total run time is often increased. In this work, we address this shortcoming with dynamic data pruning algorithms. Surprisingly, we find that uniform random dynamic pruning can outperform the prior work at aggressive pruning rates. We attribute this to the existence of "sometimes" samples -- points that are important to the learned decision boundary only some of the training time. To better exploit the subtlety of sometimes samples, we propose two algorithms, based on reinforcement learning techniques, to dynamically prune samples and achieve even higher accuracy than the random dynamic method. We test all our methods against a full-dataset baseline and the prior work on CIFAR-10 and CIFAR-100, and we can reduce the training time by up to 2x without significant performance loss. Our results suggest that data pruning should be understood as a dynamic process that is closely tied to a model's training trajectory, instead of a static step based solely on the dataset alone.