Measuring and regularizing networks in function space

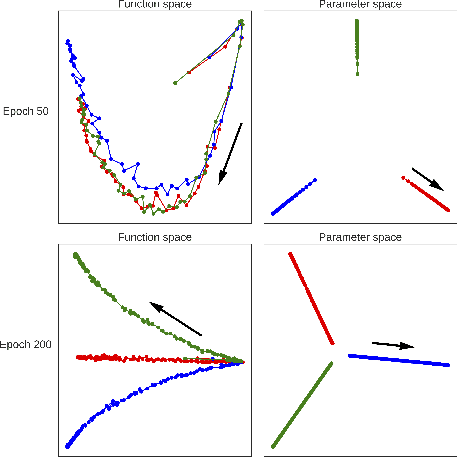
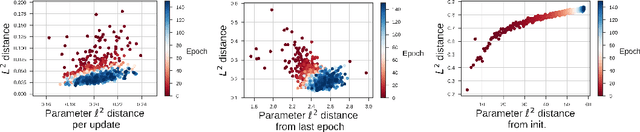
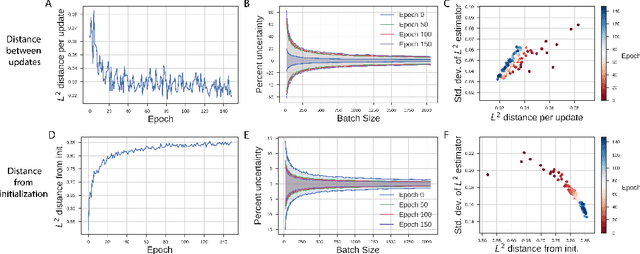
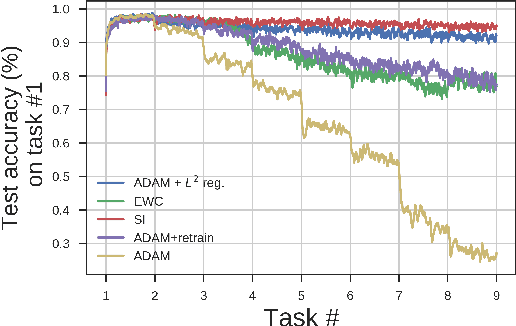
Neural network optimization is often conceptualized as optimizing parameters, but it is ultimately a matter of optimizing a function defined by inputs and outputs. However, little work has empirically evaluated network optimization in the space of possible functions and much analysis relies on Lipschitz bounds. Here, we measure the behavior of several networks in an $L^2$ Hilbert space. Lipschitz bounds appear reasonable in late optimization but not the beginning. We also observe that the function continues to change even after test error saturates. In light of this we propose a learning rule, Hilbert-constrained gradient descent (HCGD), that regularizes the distance a network can travel through $L^2$-space in any one update. HCGD should increase generalization if it is important that single updates minimally change the output function. Experiments show that HCGD reduces exploration in function space and often, but not always, improves generalization. We connect this idea to the natural gradient, which can also be derived from penalizing changes in the outputs. We conclude that decreased movement in function space is an important consideration in training neural networks.