Physics-Informed Geometry-Aware Neural Operator
Paper and Code
Aug 02, 2024
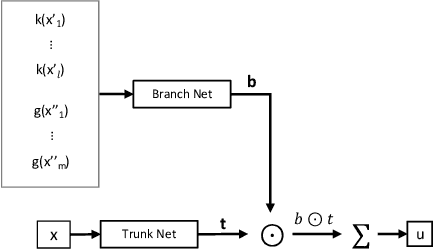
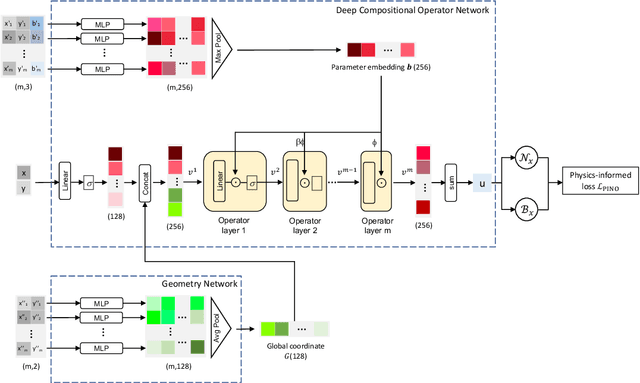

Engineering design problems often involve solving parametric Partial Differential Equations (PDEs) under variable PDE parameters and domain geometry. Recently, neural operators have shown promise in learning PDE operators and quickly predicting the PDE solutions. However, training these neural operators typically requires large datasets, the acquisition of which can be prohibitively expensive. To overcome this, physics-informed training offers an alternative way of building neural operators, eliminating the high computational costs associated with Finite Element generation of training data. Nevertheless, current physics-informed neural operators struggle with limitations, either in handling varying domain geometries or varying PDE parameters. In this research, we introduce a novel method, the Physics-Informed Geometry-Aware Neural Operator (PI-GANO), designed to simultaneously generalize across both PDE parameters and domain geometries. We adopt a geometry encoder to capture the domain geometry features, and design a novel pipeline to integrate this component within the existing DCON architecture. Numerical results demonstrate the accuracy and efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge