Design and Control of an Ultra-Slender Push-Pull Multisection Continuum Manipulator for In-Situ Inspection of Aeroengine

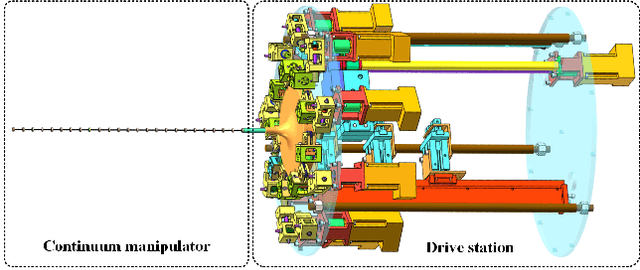
Since the shape of industrial endoscopes is passively altered according to the contact around it, manual inspection approaches of aeroengines through the inspection ports have unreachable areas, and it's difficult to traverse multistage blades and inspect them simultaneously, which requires engine disassembly or the cooperation of multiple operators, resulting in efficiency decline and increased costs. To this end, this paper proposes a novel continuum manipulator with push-pull multisection structure which provides a potential solution for the disadvantages mentioned above due to its higher flexibility, passability, and controllability in confined spaces. The ultra-slender design combined with a tendon-driven mechanism makes the manipulator acquire enough workspace and more flexible postures while maintaining a light weight. Considering the coupling between the tendons in multisection, a innovative kinematics decoupling control method is implemented, which can realize real-time control in the case of limited computational resources. A prototype is built to validate the capabilities of mechatronic design and the performance of the control algorithm. The experimental results demonstrate the advantages of our continuum manipulator in the in-situ inspection of aeroengines' multistage blades, which has the potential to be a replacement solution for industrial endoscopes.

RoboMatrix: A Skill-centric Hierarchical Framework for Scalable Robot Task Planning and Execution in Open-World

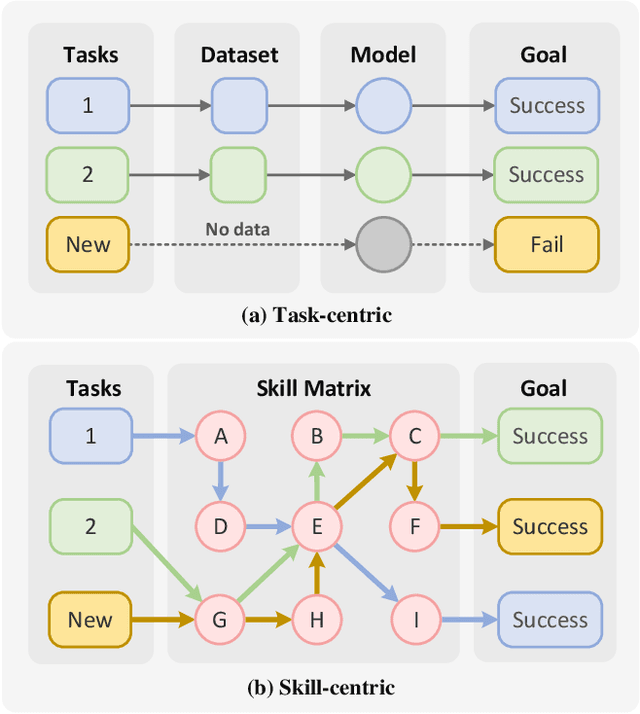
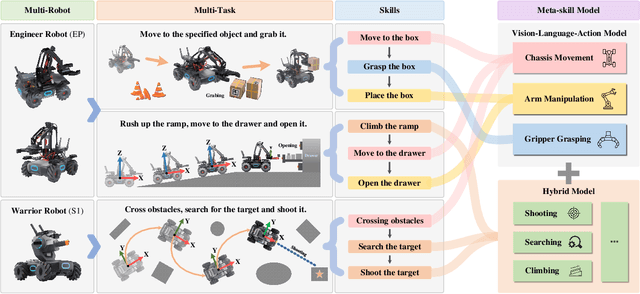
Existing policy learning methods predominantly adopt the task-centric paradigm, necessitating the collection of task data in an end-to-end manner. Consequently, the learned policy tends to fail to tackle novel tasks. Moreover, it is hard to localize the errors for a complex task with multiple stages due to end-to-end learning. To address these challenges, we propose RoboMatrix, a skill-centric and hierarchical framework for scalable task planning and execution. We first introduce a novel skill-centric paradigm that extracts the common meta-skills from different complex tasks. This allows for the capture of embodied demonstrations through a kill-centric approach, enabling the completion of open-world tasks by combining learned meta-skills. To fully leverage meta-skills, we further develop a hierarchical framework that decouples complex robot tasks into three interconnected layers: (1) a high-level modular scheduling layer; (2) a middle-level skill layer; and (3) a low-level hardware layer. Experimental results illustrate that our skill-centric and hierarchical framework achieves remarkable generalization performance across novel objects, scenes, tasks, and embodiments. This framework offers a novel solution for robot task planning and execution in open-world scenarios. Our software and hardware are available at https://github.com/WayneMao/RoboMatrix.

Physics-Informed Geometry-Aware Neural Operator

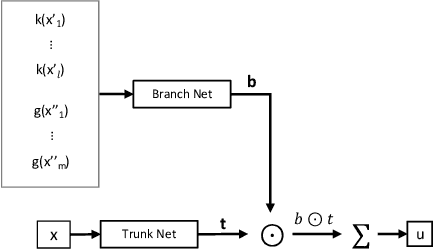
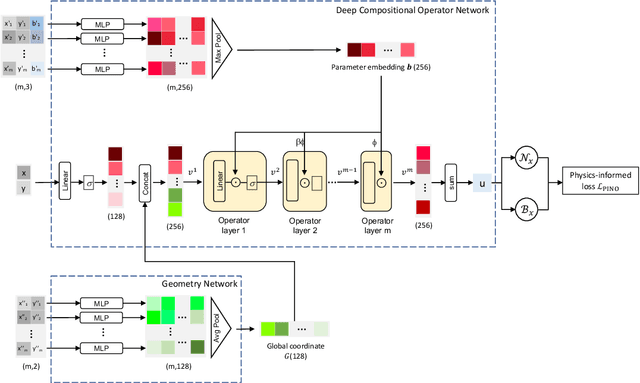
Engineering design problems often involve solving parametric Partial Differential Equations (PDEs) under variable PDE parameters and domain geometry. Recently, neural operators have shown promise in learning PDE operators and quickly predicting the PDE solutions. However, training these neural operators typically requires large datasets, the acquisition of which can be prohibitively expensive. To overcome this, physics-informed training offers an alternative way of building neural operators, eliminating the high computational costs associated with Finite Element generation of training data. Nevertheless, current physics-informed neural operators struggle with limitations, either in handling varying domain geometries or varying PDE parameters. In this research, we introduce a novel method, the Physics-Informed Geometry-Aware Neural Operator (PI-GANO), designed to simultaneously generalize across both PDE parameters and domain geometries. We adopt a geometry encoder to capture the domain geometry features, and design a novel pipeline to integrate this component within the existing DCON architecture. Numerical results demonstrate the accuracy and efficiency of the proposed method.

Physics-informed Mesh-independent Deep Compositional Operator Network

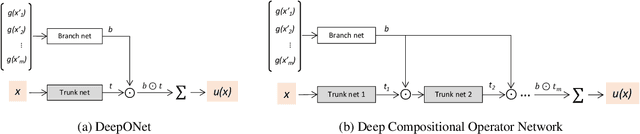
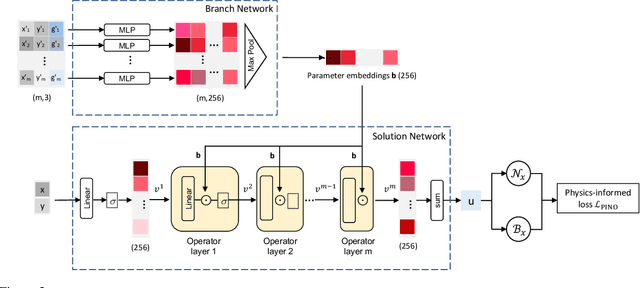
Solving parametric Partial Differential Equations (PDEs) for a broad range of parameters is a critical challenge in scientific computing. To this end, neural operators, which learn mappings from parameters to solutions, have been successfully used. However, the training of neural operators typically demands large training datasets, the acquisition of which can be prohibitively expensive. To address this challenge, physics-informed training can offer a cost-effective strategy. However, current physics-informed neural operators face limitations, either in handling irregular domain shapes or in generalization to various discretizations of PDE parameters with variable mesh sizes. In this research, we introduce a novel physics-informed model architecture which can generalize to parameter discretizations of variable size and irregular domain shapes. Particularly, inspired by deep operator neural networks, our model involves a discretization-independent learning of parameter embedding repeatedly, and this parameter embedding is integrated with the response embeddings through multiple compositional layers, for more expressivity. Numerical results demonstrate the accuracy and efficiency of the proposed method.

Attention-based Spatial-Temporal Graph Neural ODE for Traffic Prediction

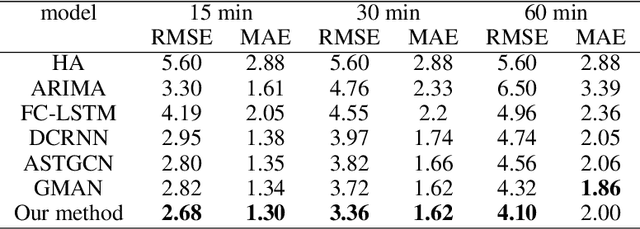
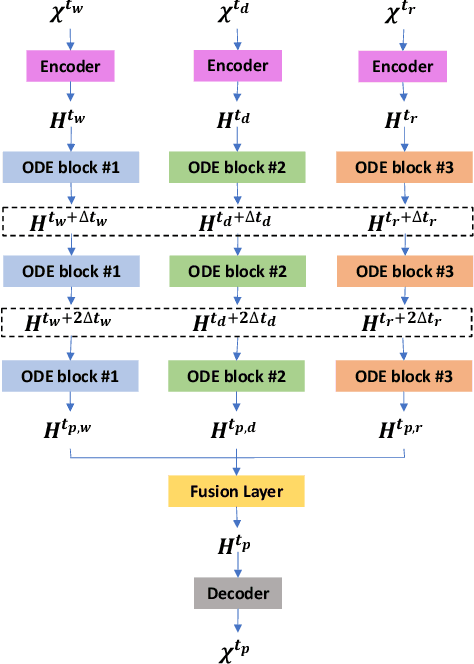
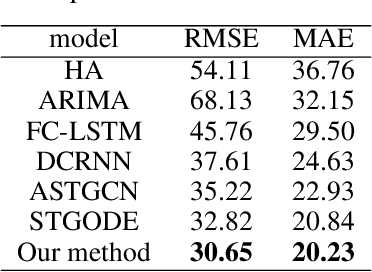
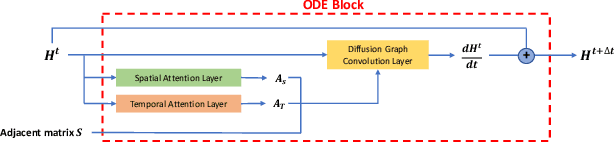
Traffic forecasting is an important issue in intelligent traffic systems (ITS). Graph neural networks (GNNs) are effective deep learning models to capture the complex spatio-temporal dependency of traffic data, achieving ideal prediction performance. In this paper, we propose attention-based graph neural ODE (ASTGODE) that explicitly learns the dynamics of the traffic system, which makes the prediction of our machine learning model more explainable. Our model aggregates traffic patterns of different periods and has satisfactory performance on two real-world traffic data sets. The results show that our model achieves the highest accuracy of the root mean square error metric among all the existing GNN models in our experiments.

Explainable Graph Pyramid Autoformer for Long-Term Traffic Forecasting

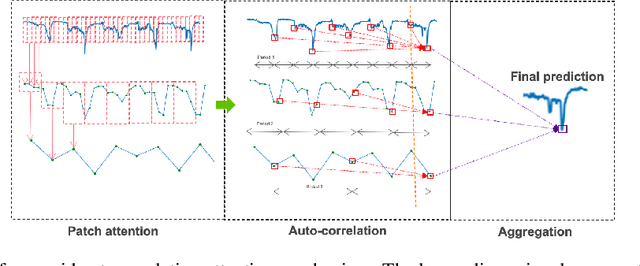
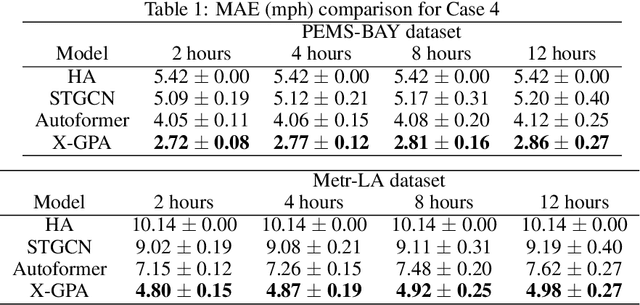
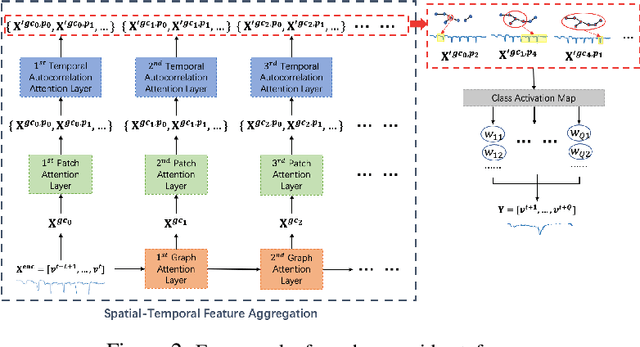
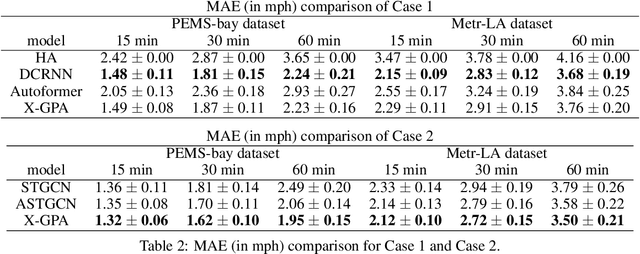
Accurate traffic forecasting is vital to an intelligent transportation system. Although many deep learning models have achieved state-of-art performance for short-term traffic forecasting of up to 1 hour, long-term traffic forecasting that spans multiple hours remains a major challenge. Moreover, most of the existing deep learning traffic forecasting models are black box, presenting additional challenges related to explainability and interpretability. We develop Graph Pyramid Autoformer (X-GPA), an explainable attention-based spatial-temporal graph neural network that uses a novel pyramid autocorrelation attention mechanism. It enables learning from long temporal sequences on graphs and improves long-term traffic forecasting accuracy. Our model can achieve up to 35 % better long-term traffic forecast accuracy than that of several state-of-the-art methods. The attention-based scores from the X-GPA model provide spatial and temporal explanations based on the traffic dynamics, which change for normal vs. peak-hour traffic and weekday vs. weekend traffic.

PI-VAE: Physics-Informed Variational Auto-Encoder for stochastic differential equations

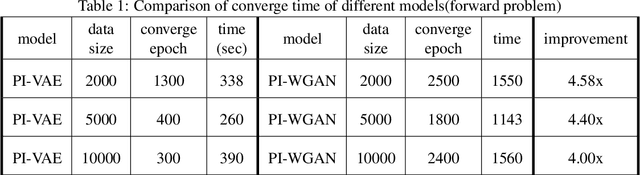
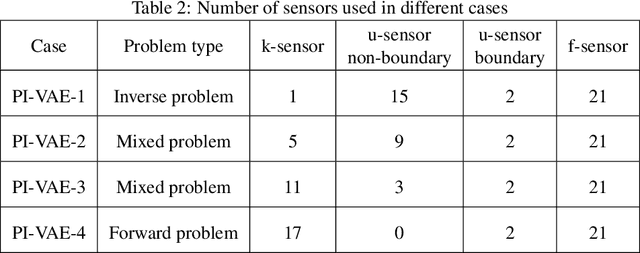
We propose a new class of physics-informed neural networks, called physics-informed Variational Autoencoder (PI-VAE), to solve stochastic differential equations (SDEs) or inverse problems involving SDEs. In these problems the governing equations are known but only a limited number of measurements of system parameters are available. PI-VAE consists of a variational autoencoder (VAE), which generates samples of system variables and parameters. This generative model is integrated with the governing equations. In this integration, the derivatives of VAE outputs are readily calculated using automatic differentiation, and used in the physics-based loss term. In this work, the loss function is chosen to be the Maximum Mean Discrepancy (MMD) for improved performance, and neural network parameters are updated iteratively using the stochastic gradient descent algorithm. We first test the proposed method on approximating stochastic processes. Then we study three types of problems related to SDEs: forward and inverse problems together with mixed problems where system parameters and solutions are simultaneously calculated. The satisfactory accuracy and efficiency of the proposed method are numerically demonstrated in comparison with physics-informed generative adversarial network (PI-WGAN).