Physics-informed Mesh-independent Deep Compositional Operator Network
Paper and Code
Apr 21, 2024
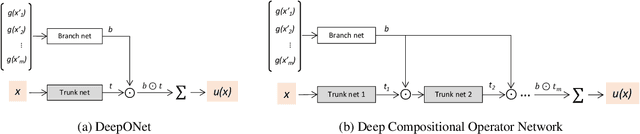
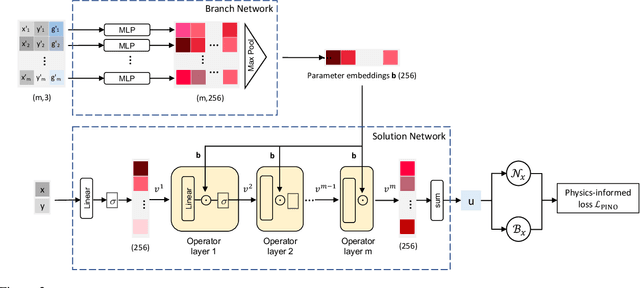

Solving parametric Partial Differential Equations (PDEs) for a broad range of parameters is a critical challenge in scientific computing. To this end, neural operators, which learn mappings from parameters to solutions, have been successfully used. However, the training of neural operators typically demands large training datasets, the acquisition of which can be prohibitively expensive. To address this challenge, physics-informed training can offer a cost-effective strategy. However, current physics-informed neural operators face limitations, either in handling irregular domain shapes or in generalization to various discretizations of PDE parameters with variable mesh sizes. In this research, we introduce a novel physics-informed model architecture which can generalize to parameter discretizations of variable size and irregular domain shapes. Particularly, inspired by deep operator neural networks, our model involves a discretization-independent learning of parameter embedding repeatedly, and this parameter embedding is integrated with the response embeddings through multiple compositional layers, for more expressivity. Numerical results demonstrate the accuracy and efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge