Structure and Distribution Metric for Quantifying the Quality of Uncertainty: Assessing Gaussian Processes, Deep Neural Nets, and Deep Neural Operators for Regression
Paper and Code
Mar 09, 2022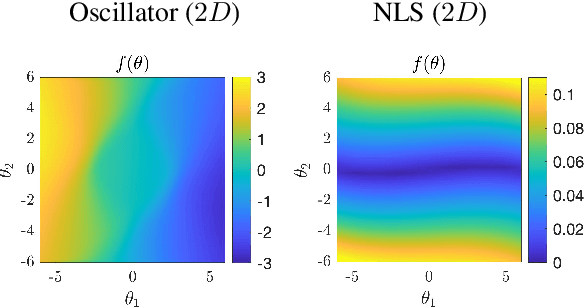
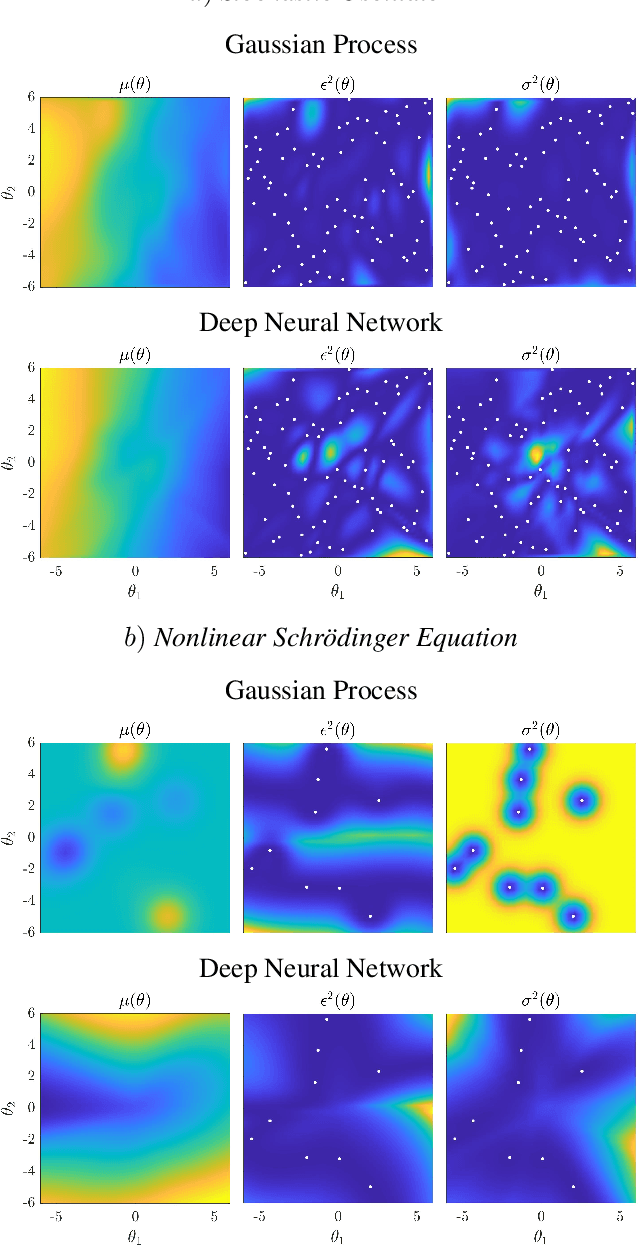
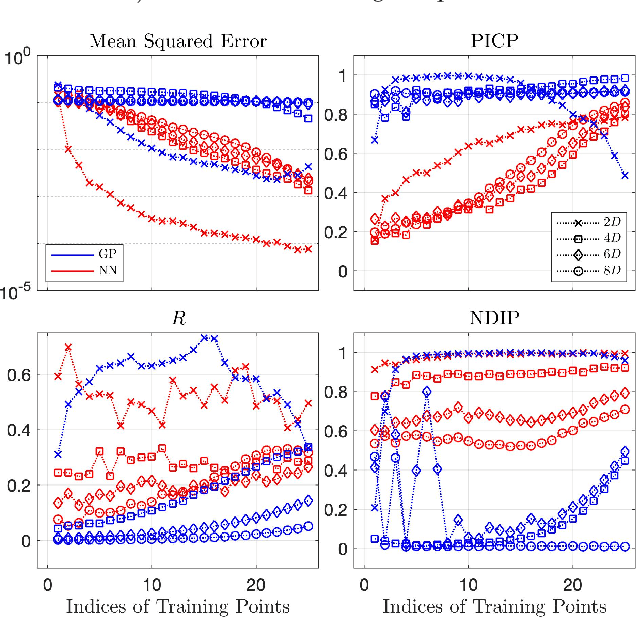
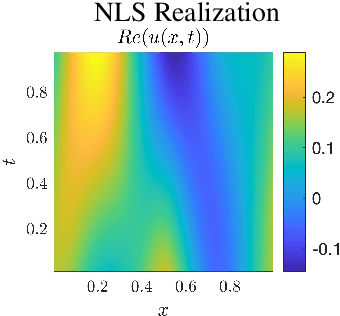
We propose two bounded comparison metrics that may be implemented to arbitrary dimensions in regression tasks. One quantifies the structure of uncertainty and the other quantifies the distribution of uncertainty. The structure metric assesses the similarity in shape and location of uncertainty with the true error, while the distribution metric quantifies the supported magnitudes between the two. We apply these metrics to Gaussian Processes (GPs), Ensemble Deep Neural Nets (DNNs), and Ensemble Deep Neural Operators (DNOs) on high-dimensional and nonlinear test cases. We find that comparing a model's uncertainty estimates with the model's squared error provides a compelling ground truth assessment. We also observe that both DNNs and DNOs, especially when compared to GPs, provide encouraging metric values in high dimensions with either sparse or plentiful data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge