The Landscape of Causal Discovery Data: Grounding Causal Discovery in Real-World Applications

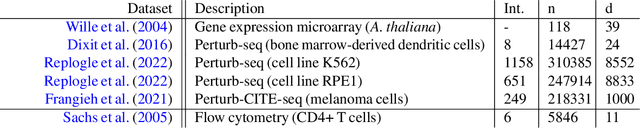
Causal discovery aims to automatically uncover causal relationships from data, a capability with significant potential across many scientific disciplines. However, its real-world applications remain limited. Current methods often rely on unrealistic assumptions and are evaluated only on simple synthetic toy datasets, often with inadequate evaluation metrics. In this paper, we substantiate these claims by performing a systematic review of the recent causal discovery literature. We present applications in biology, neuroscience, and Earth sciences - fields where causal discovery holds promise for addressing key challenges. We highlight available simulated and real-world datasets from these domains and discuss common assumption violations that have spurred the development of new methods. Our goal is to encourage the community to adopt better evaluation practices by utilizing realistic datasets and more adequate metrics.

Probably approximately correct high-dimensional causal effect estimation given a valid adjustment set

Accurate estimates of causal effects play a key role in decision-making across applications such as healthcare, economics, and operations. In the absence of randomized experiments, a common approach to estimating causal effects uses \textit{covariate adjustment}. In this paper, we study covariate adjustment for discrete distributions from the PAC learning perspective, assuming knowledge of a valid adjustment set $\bZ$, which might be high-dimensional. Our first main result PAC-bounds the estimation error of covariate adjustment by a term that is exponential in the size of the adjustment set; it is known that such a dependency is unavoidable even if one only aims to minimize the mean squared error. Motivated by this result, we introduce the notion of an \emph{$\eps$-Markov blanket}, give bounds on the misspecification error of using such a set for covariate adjustment, and provide an algorithm for $\eps$-Markov blanket discovery; our second main result upper bounds the sample complexity of this algorithm. Furthermore, we provide a misspecification error bound and a constraint-based algorithm that allow us to go beyond $\eps$-Markov blankets to even smaller adjustment sets. Our third main result upper bounds the sample complexity of this algorithm, and our final result combines the first three into an overall PAC bound. Altogether, our results highlight that one does not need to perfectly recover causal structure in order to ensure accurate estimates of causal effects.

Synthetic Potential Outcomes for Mixtures of Treatment Effects

Modern data analysis frequently relies on the use of large datasets, often constructed as amalgamations of diverse populations or data-sources. Heterogeneity across these smaller datasets constitutes two major challenges for causal inference: (1) the source of each sample can introduce latent confounding between treatment and effect, and (2) diverse populations may respond differently to the same treatment, giving rise to heterogeneous treatment effects (HTEs). The issues of latent confounding and HTEs have been studied separately but not in conjunction. In particular, previous works only report the conditional average treatment effect (CATE) among similar individuals (with respect to the measured covariates). CATEs cannot resolve mixtures of potential treatment effects driven by latent heterogeneity, which we call mixtures of treatment effects (MTEs). Inspired by method of moment approaches to mixture models, we propose "synthetic potential outcomes" (SPOs). Our new approach deconfounds heterogeneity while also guaranteeing the identifiability of MTEs. This technique bypasses full recovery of a mixture, which significantly simplifies its requirements for identifiability. We demonstrate the efficacy of SPOs on synthetic data.

Causal Imputation for Counterfactual SCMs: Bridging Graphs and Latent Factor Models

We consider the task of causal imputation, where we aim to predict the outcomes of some set of actions across a wide range of possible contexts. As a running example, we consider predicting how different drugs affect cells from different cell types. We study the index-only setting, where the actions and contexts are categorical variables with a finite number of possible values. Even in this simple setting, a practical challenge arises, since often only a small subset of possible action-context pairs have been studied. Thus, models must extrapolate to novel action-context pairs, which can be framed as a form of matrix completion with rows indexed by actions, columns indexed by contexts, and matrix entries corresponding to outcomes. We introduce a novel SCM-based model class, where the outcome is expressed as a counterfactual, actions are expressed as interventions on an instrumental variable, and contexts are defined based on the initial state of the system. We show that, under a linearity assumption, this setup induces a latent factor model over the matrix of outcomes, with an additional fixed effect term. To perform causal prediction based on this model class, we introduce simple extension to the Synthetic Interventions estimator (Agarwal et al., 2020). We evaluate several matrix completion approaches on the PRISM drug repurposing dataset, showing that our method outperforms all other considered matrix completion approaches.

Identifiability Guarantees for Causal Disentanglement from Soft Interventions

Causal disentanglement aims to uncover a representation of data using latent variables that are interrelated through a causal model. Such a representation is identifiable if the latent model that explains the data is unique. In this paper, we focus on the scenario where unpaired observational and interventional data are available, with each intervention changing the mechanism of a latent variable. When the causal variables are fully observed, statistically consistent algorithms have been developed to identify the causal model under faithfulness assumptions. We here show that identifiability can still be achieved with unobserved causal variables, given a generalized notion of faithfulness. Our results guarantee that we can recover the latent causal model up to an equivalence class and predict the effect of unseen combinations of interventions, in the limit of infinite data. We implement our causal disentanglement framework by developing an autoencoding variational Bayes algorithm and apply it to the problem of predicting combinatorial perturbation effects in genomics.

Unpaired Multi-Domain Causal Representation Learning

The goal of causal representation learning is to find a representation of data that consists of causally related latent variables. We consider a setup where one has access to data from multiple domains that potentially share a causal representation. Crucially, observations in different domains are assumed to be unpaired, that is, we only observe the marginal distribution in each domain but not their joint distribution. In this paper, we give sufficient conditions for identifiability of the joint distribution and the shared causal graph in a linear setup. Identifiability holds if we can uniquely recover the joint distribution and the shared causal representation from the marginal distributions in each domain. We transform our identifiability results into a practical method to recover the shared latent causal graph. Moreover, we study how multiple domains reduce errors in falsely detecting shared causal variables in the finite data setting.

Linear Causal Disentanglement via Interventions

Causal disentanglement seeks a representation of data involving latent variables that relate to one another via a causal model. A representation is identifiable if both the latent model and the transformation from latent to observed variables are unique. In this paper, we study observed variables that are a linear transformation of a linear latent causal model. Data from interventions are necessary for identifiability: if one latent variable is missing an intervention, we show that there exist distinct models that cannot be distinguished. Conversely, we show that a single intervention on each latent variable is sufficient for identifiability. Our proof uses a generalization of the RQ decomposition of a matrix that replaces the usual orthogonal and upper triangular conditions with analogues depending on a partial order on the rows of the matrix, with partial order determined by a latent causal model. We corroborate our theoretical results with a method for causal disentanglement that accurately recovers a latent causal model.

Active Learning for Optimal Intervention Design in Causal Models

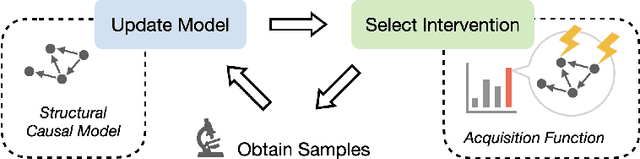
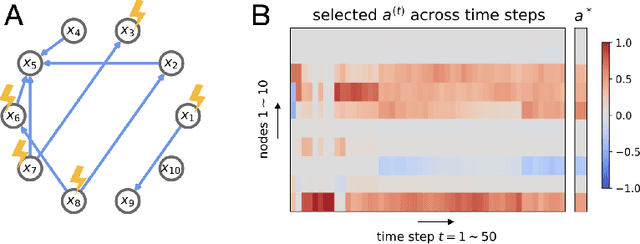
An important problem across disciplines is the discovery of interventions that produce a desired outcome. When the space of possible interventions is large, making an exhaustive search infeasible, experimental design strategies are needed. In this context, encoding the causal relationships between the variables, and thus the effect of interventions on the system, is critical in order to identify desirable interventions efficiently. We develop an iterative causal method to identify optimal interventions, as measured by the discrepancy between the post-interventional mean of the distribution and a desired target mean. We formulate an active learning strategy that uses the samples obtained so far from different interventions to update the belief about the underlying causal model, as well as to identify samples that are most informative about optimal interventions and thus should be acquired in the next batch. The approach employs a Bayesian update for the causal model and prioritizes interventions using a carefully designed, causally informed acquisition function. This acquisition function is evaluated in closed form, allowing for efficient optimization. The resulting algorithms are theoretically grounded with information-theoretic bounds and provable consistency results. We illustrate the method on both synthetic data and real-world biological data, namely gene expression data from Perturb-CITE-seq experiments, to identify optimal perturbations that induce a specific cell state transition; the proposed causal approach is observed to achieve better sample efficiency compared to several baselines. In both cases we observe that the causally informed acquisition function notably outperforms existing criteria allowing for optimal intervention design with significantly less experiments.

Causal Structure Learning: a Combinatorial Perspective

In this review, we discuss approaches for learning causal structure from data, also called causal discovery. In particular, we focus on approaches for learning directed acyclic graphs (DAGs) and various generalizations which allow for some variables to be unobserved in the available data. We devote special attention to two fundamental combinatorial aspects of causal structure learning. First, we discuss the structure of the search space over causal graphs. Second, we discuss the structure of equivalence classes over causal graphs, i.e., sets of graphs which represent what can be learned from observational data alone, and how these equivalence classes can be refined by adding interventional data.

Matching a Desired Causal State via Shift Interventions

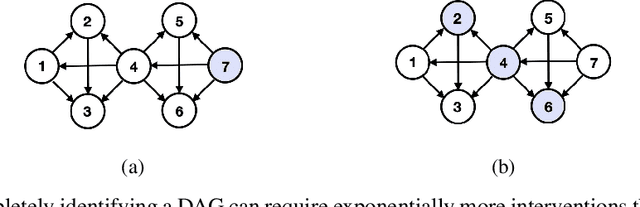
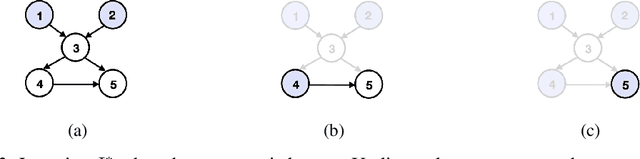
Transforming a causal system from a given initial state to a desired target state is an important task permeating multiple fields including control theory, biology, and materials science. In causal models, such transformations can be achieved by performing a set of interventions. In this paper, we consider the problem of identifying a shift intervention that matches the desired mean of a system through active learning. We define the Markov equivalence class that is identifiable from shift interventions and propose two active learning strategies that are guaranteed to exactly match a desired mean. We then derive a worst-case lower bound for the number of interventions required and show that these strategies are optimal for certain classes of graphs. In particular, we show that our strategies may require exponentially fewer interventions than the previously considered approaches, which optimize for structure learning in the underlying causal graph. In line with our theoretical results, we also demonstrate experimentally that our proposed active learning strategies require fewer interventions compared to several baselines.