Active Learning for Optimal Intervention Design in Causal Models
Paper and Code
Sep 10, 2022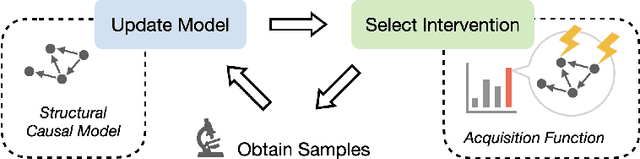
An important problem across disciplines is the discovery of interventions that produce a desired outcome. When the space of possible interventions is large, making an exhaustive search infeasible, experimental design strategies are needed. In this context, encoding the causal relationships between the variables, and thus the effect of interventions on the system, is critical in order to identify desirable interventions efficiently. We develop an iterative causal method to identify optimal interventions, as measured by the discrepancy between the post-interventional mean of the distribution and a desired target mean. We formulate an active learning strategy that uses the samples obtained so far from different interventions to update the belief about the underlying causal model, as well as to identify samples that are most informative about optimal interventions and thus should be acquired in the next batch. The approach employs a Bayesian update for the causal model and prioritizes interventions using a carefully designed, causally informed acquisition function. This acquisition function is evaluated in closed form, allowing for efficient optimization. The resulting algorithms are theoretically grounded with information-theoretic bounds and provable consistency results. We illustrate the method on both synthetic data and real-world biological data, namely gene expression data from Perturb-CITE-seq experiments, to identify optimal perturbations that induce a specific cell state transition; the proposed causal approach is observed to achieve better sample efficiency compared to several baselines. In both cases we observe that the causally informed acquisition function notably outperforms existing criteria allowing for optimal intervention design with significantly less experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge