Meta-Dependence in Conditional Independence Testing

Constraint-based causal discovery algorithms utilize many statistical tests for conditional independence to uncover networks of causal dependencies. These approaches to causal discovery rely on an assumed correspondence between the graphical properties of a causal structure and the conditional independence properties of observed variables, known as the causal Markov condition and faithfulness. Finite data yields an empirical distribution that is "close" to the actual distribution. Across these many possible empirical distributions, the correspondence to the graphical properties can break down for different conditional independencies, and multiple violations can occur at the same time. We study this "meta-dependence" between conditional independence properties using the following geometric intuition: each conditional independence property constrains the space of possible joint distributions to a manifold. The "meta-dependence" between conditional independences is informed by the position of these manifolds relative to the true probability distribution. We provide a simple-to-compute measure of this meta-dependence using information projections and consolidate our findings empirically using both synthetic and real-world data.

Synthetic Potential Outcomes for Mixtures of Treatment Effects

Modern data analysis frequently relies on the use of large datasets, often constructed as amalgamations of diverse populations or data-sources. Heterogeneity across these smaller datasets constitutes two major challenges for causal inference: (1) the source of each sample can introduce latent confounding between treatment and effect, and (2) diverse populations may respond differently to the same treatment, giving rise to heterogeneous treatment effects (HTEs). The issues of latent confounding and HTEs have been studied separately but not in conjunction. In particular, previous works only report the conditional average treatment effect (CATE) among similar individuals (with respect to the measured covariates). CATEs cannot resolve mixtures of potential treatment effects driven by latent heterogeneity, which we call mixtures of treatment effects (MTEs). Inspired by method of moment approaches to mixture models, we propose "synthetic potential outcomes" (SPOs). Our new approach deconfounds heterogeneity while also guaranteeing the identifiability of MTEs. This technique bypasses full recovery of a mixture, which significantly simplifies its requirements for identifiability. We demonstrate the efficacy of SPOs on synthetic data.

Causal Discovery under Latent Class Confounding

Directed acyclic graphs are used to model the causal structure of a system. ``Causal discovery'' describes the problem of learning this structure from data. When data is an aggregate from multiple sources (populations or environments), global confounding obscures conditional independence properties that drive many causal discovery algorithms. For this reason, existing causal discovery algorithms are not suitable for the multiple-source setting. We demonstrate that, if the confounding is of bounded cardinality (i.e. the data comes from a limited number of sources), causal discovery can still be achieved. The feasibility of this problem is governed by a trade-off between the cardinality of the global confounder, the cardinalities of the observed variables, and the sparsity of the causal structure.

Distribution Re-weighting and Voting Paradoxes

We explore a specific type of distribution shift called domain expertise, in which training is limited to a subset of all possible labels. This setting is common among specialized human experts, or specific focused studies. We show how the standard approach to distribution shift, which involves re-weighting data, can result in paradoxical disagreements among differing domain expertise. We also demonstrate how standard adjustments for causal inference lead to the same paradox. We prove that the characteristics of these paradoxes exactly mimic another set of paradoxes which arise among sets of voter preferences.

Identification of Mixtures of Discrete Product Distributions in Near-Optimal Sample and Time Complexity

We consider the problem of identifying, from statistics, a distribution of discrete random variables $X_1,\ldots,X_n$ that is a mixture of $k$ product distributions. The best previous sample complexity for $n \in O(k)$ was $(1/\zeta)^{O(k^2 \log k)}$ (under a mild separation assumption parameterized by $\zeta$). The best known lower bound was $\exp(\Omega(k))$. It is known that $n\geq 2k-1$ is necessary and sufficient for identification. We show, for any $n\geq 2k-1$, how to achieve sample complexity and run-time complexity $(1/\zeta)^{O(k)}$. We also extend the known lower bound of $e^{\Omega(k)}$ to match our upper bound across a broad range of $\zeta$. Our results are obtained by combining (a) a classic method for robust tensor decomposition, (b) a novel way of bounding the condition number of key matrices called Hadamard extensions, by studying their action only on flattened rank-1 tensors.

Causal Information Splitting: Engineering Proxy Features for Robustness to Distribution Shifts

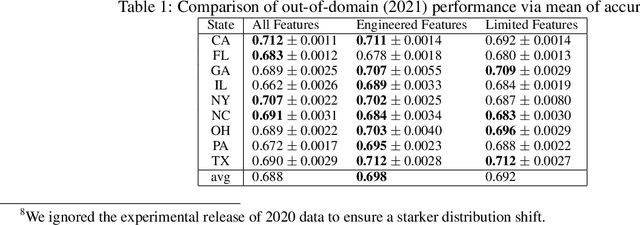
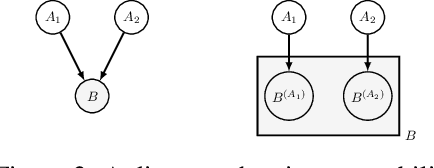
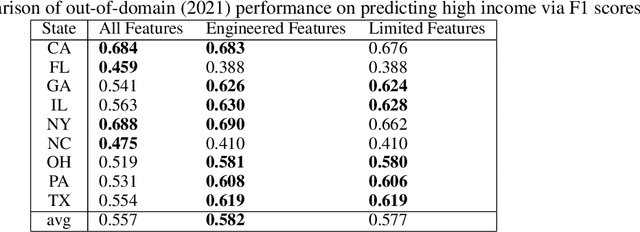
Statistical prediction models are often trained on data that is drawn from different probability distributions than their eventual use cases. One approach to proactively prepare for these shifts harnesses the intuition that causal mechanisms should remain invariant between environments. Here we focus on a challenging setting in which the causal and anticausal variables of the target are unobserved. Leaning on information theory, we develop feature selection and engineering techniques for the observed downstream variables that act as proxies. We identify proxies that help to build stable models and moreover utilize auxiliary training tasks to extract stability-enhancing information from proxies. We demonstrate the effectiveness of our techniques on synthetic and real data.

Identifying Mixtures of Bayesian Network Distributions

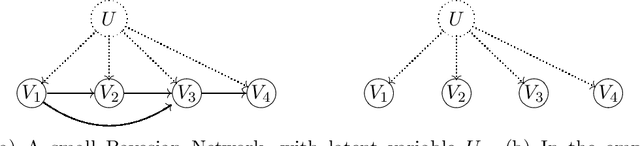
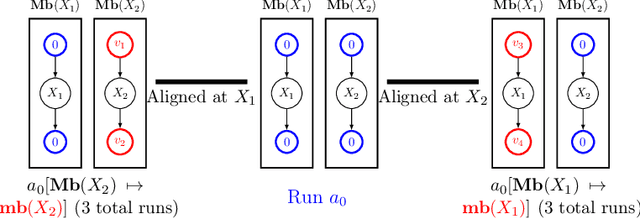
A Bayesian Network is a directed acyclic graph (DAG) on a set of $n$ random variables (identified with the vertices); a Bayesian Network Distribution (BND) is a probability distribution on the rv's that is Markovian on the graph. A finite mixture of such models is the projection on these variables of a BND on the larger graph which has an additional "hidden" (or "latent") random variable $U$, ranging in $\{1,\ldots,k\}$, and a directed edge from $U$ to every other vertex. Models of this type are fundamental to research in Causal Inference, where $U$ models a confounding effect. One extremely special case has been of longstanding interest in the theory literature: the empty graph. Such a distribution is simply a mixture of $k$ product distributions. A longstanding problem has been, given the joint distribution of a mixture of $k$ product distributions, to identify each of the product distributions, and their mixture weights. Our results are: (1) We improve the sample complexity (and runtime) for identifying mixtures of $k$ product distributions from $\exp(O(k^2))$ to $\exp(O(k \log k))$. This is almost best possible in view of a known $\exp(\Omega(k))$ lower bound. (2) We give the first algorithm for the case of non-empty graphs. The complexity for a graph of maximum degree $\Delta$ is $\exp(O(k(\Delta^2 + \log k)))$. (The above complexities are approximate and suppress dependence on secondary parameters.)

Expert Graphs: Synthesizing New Expertise via Collaboration

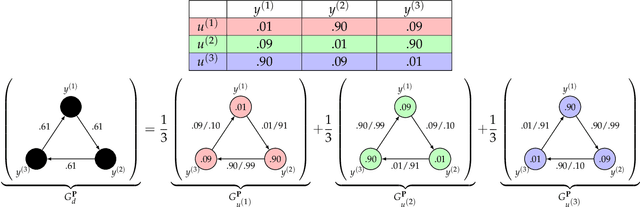
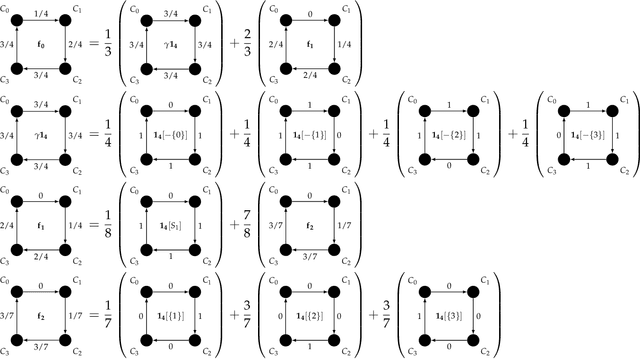
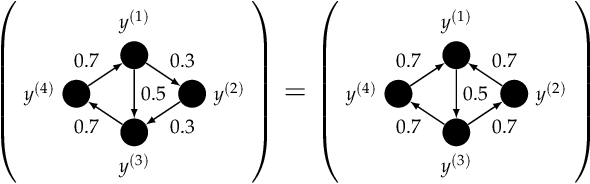
Consider multiple experts with overlapping expertise working on a classification problem under uncertain input. What constitutes a consistent set of opinions? How can we predict the opinions of experts on missing sub-domains? In this paper, we define a framework of to analyze this problem, termed "expert graphs." In an expert graph, vertices represent classes and edges represent binary opinions on the topics of their vertices. We derive necessary conditions for expert graph validity and use them to create "synthetic experts" which describe opinions consistent with the observed opinions of other experts. We show this framework to be equivalent to the well-studied linear ordering polytope. We show our conditions are not sufficient for describing all expert graphs on cliques, but are sufficient for cycles.

Source Identification for Mixtures of Product Distributions

We give an algorithm for source identification of a mixture of $k$ product distributions on $n$ bits. This is a fundamental problem in machine learning with many applications. Our algorithm identifies the source parameters of an identifiable mixture, given, as input, approximate values of multilinear moments (derived, for instance, from a sufficiently large sample), using $2^{O(k^2)} n^{O(k)}$ arithmetic operations. Our result is the first explicit bound on the computational complexity of source identification of such mixtures. The running time improves previous results by Feldman, O'Donnell, and Servedio (FOCS 2005) and Chen and Moitra (STOC 2019) that guaranteed only learning the mixture (without parametric identification of the source). Our analysis gives a quantitative version of a qualitative characterization of identifiable sources that is due to Tahmasebi, Motahari, and Maddah-Ali (ISIT 2018).

Robust Correction of Sampling Bias Using Cumulative Distribution Functions

Varying domains and biased datasets can lead to differences between the training and the target distributions, known as covariate shift. Current approaches for alleviating this often rely on estimating the ratio of training and target probability density functions. These techniques require parameter tuning and can be unstable across different datasets. We present a new method for handling covariate shift using the empirical cumulative distribution function estimates of the target distribution by a rigorous generalization of a recent idea proposed by Vapnik and Izmailov. Further, we show experimentally that our method is more robust in its predictions, is not reliant on parameter tuning and shows similar classification performance compared to the current state-of-the-art techniques on synthetic and real datasets.