Expert Graphs: Synthesizing New Expertise via Collaboration
Paper and Code
Jul 15, 2021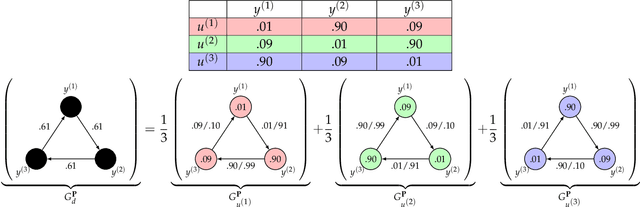

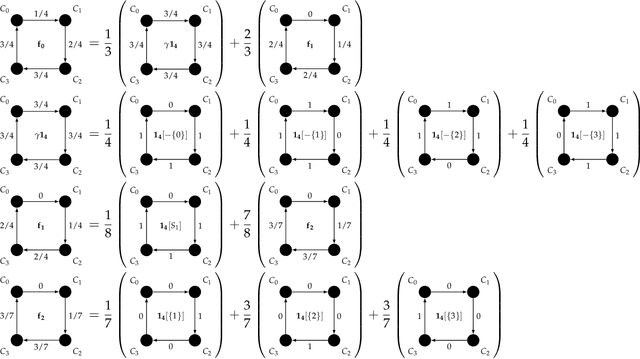
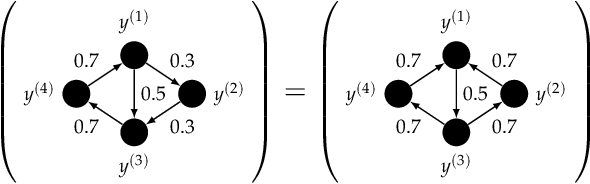
Consider multiple experts with overlapping expertise working on a classification problem under uncertain input. What constitutes a consistent set of opinions? How can we predict the opinions of experts on missing sub-domains? In this paper, we define a framework of to analyze this problem, termed "expert graphs." In an expert graph, vertices represent classes and edges represent binary opinions on the topics of their vertices. We derive necessary conditions for expert graph validity and use them to create "synthetic experts" which describe opinions consistent with the observed opinions of other experts. We show this framework to be equivalent to the well-studied linear ordering polytope. We show our conditions are not sufficient for describing all expert graphs on cliques, but are sufficient for cycles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge