Nearest Neighbor Representations of Neural Circuits

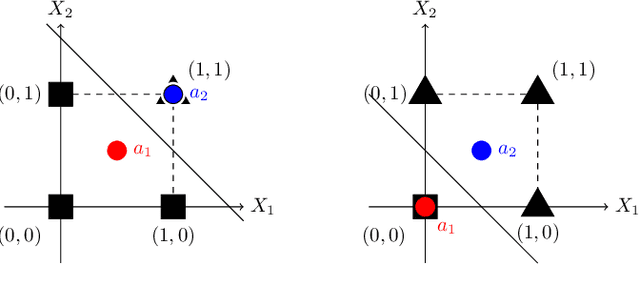
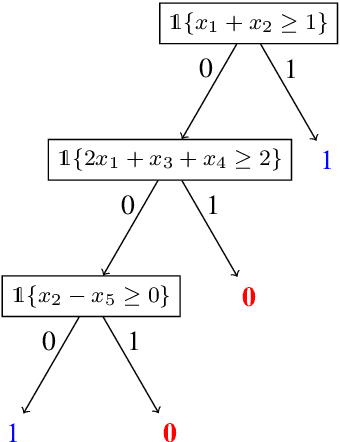
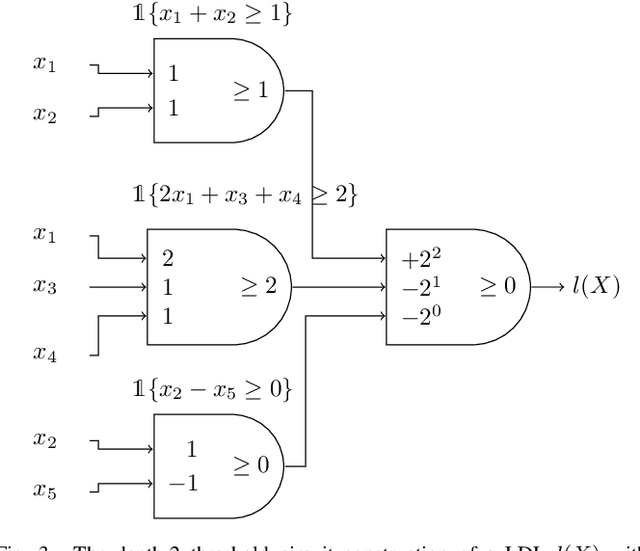
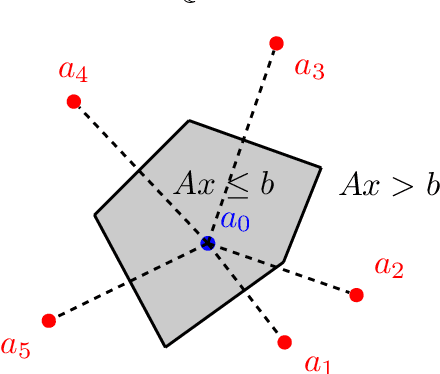
Neural networks successfully capture the computational power of the human brain for many tasks. Similarly inspired by the brain architecture, Nearest Neighbor (NN) representations is a novel approach of computation. We establish a firmer correspondence between NN representations and neural networks. Although it was known how to represent a single neuron using NN representations, there were no results even for small depth neural networks. Specifically, for depth-2 threshold circuits, we provide explicit constructions for their NN representation with an explicit bound on the number of bits to represent it. Example functions include NN representations of convex polytopes (AND of threshold gates), IP2, OR of threshold gates, and linear or exact decision lists.

Nearest Neighbor Representations of Neurons

The Nearest Neighbor (NN) Representation is an emerging computational model that is inspired by the brain. We study the complexity of representing a neuron (threshold function) using the NN representations. It is known that two anchors (the points to which NN is computed) are sufficient for a NN representation of a threshold function, however, the resolution (the maximum number of bits required for the entries of an anchor) is $O(n\log{n})$. In this work, the trade-off between the number of anchors and the resolution of a NN representation of threshold functions is investigated. We prove that the well-known threshold functions EQUALITY, COMPARISON, and ODD-MAX-BIT, which require 2 or 3 anchors and resolution of $O(n)$, can be represented by polynomially large number of anchors in $n$ and $O(\log{n})$ resolution. We conjecture that for all threshold functions, there are NN representations with polynomially large size and logarithmic resolution in $n$.

Distribution Re-weighting and Voting Paradoxes

We explore a specific type of distribution shift called domain expertise, in which training is limited to a subset of all possible labels. This setting is common among specialized human experts, or specific focused studies. We show how the standard approach to distribution shift, which involves re-weighting data, can result in paradoxical disagreements among differing domain expertise. We also demonstrate how standard adjustments for causal inference lead to the same paradox. We prove that the characteristics of these paradoxes exactly mimic another set of paradoxes which arise among sets of voter preferences.

On the Information Capacity of Nearest Neighbor Representations

The $\textit{von Neumann Computer Architecture}$ has a distinction between computation and memory. In contrast, the brain has an integrated architecture where computation and memory are indistinguishable. Motivated by the architecture of the brain, we propose a model of $\textit{associative computation}$ where memory is defined by a set of vectors in $\mathbb{R}^n$ (that we call $\textit{anchors}$), computation is performed by convergence from an input vector to a nearest neighbor anchor, and the output is a label associated with an anchor. Specifically, in this paper, we study the representation of Boolean functions in the associative computation model, where the inputs are binary vectors and the corresponding outputs are the labels ($0$ or $1$) of the nearest neighbor anchors. The information capacity of a Boolean function in this model is associated with two quantities: $\textit{(i)}$ the number of anchors (called $\textit{Nearest Neighbor (NN) Complexity}$) and $\textit{(ii)}$ the maximal number of bits representing entries of anchors (called $\textit{Resolution}$). We study symmetric Boolean functions and present constructions that have optimal NN complexity and resolution.

On Algebraic Constructions of Neural Networks with Small Weights

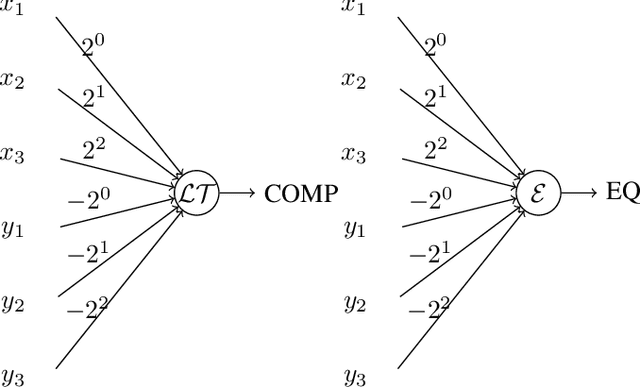
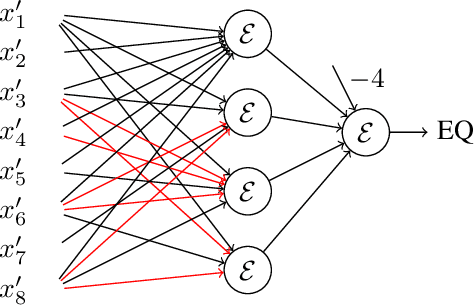
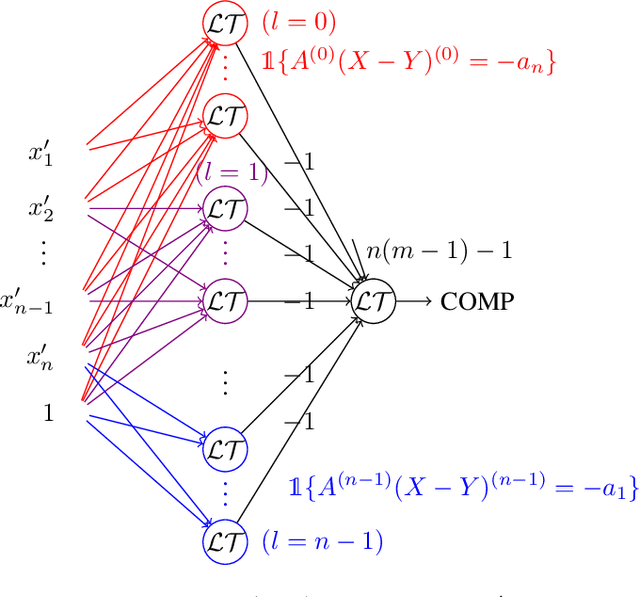
Neural gates compute functions based on weighted sums of the input variables. The expressive power of neural gates (number of distinct functions it can compute) depends on the weight sizes and, in general, large weights (exponential in the number of inputs) are required. Studying the trade-offs among the weight sizes, circuit size and depth is a well-studied topic both in circuit complexity theory and the practice of neural computation. We propose a new approach for studying these complexity trade-offs by considering a related algebraic framework. Specifically, given a single linear equation with arbitrary coefficients, we would like to express it using a system of linear equations with smaller (even constant) coefficients. The techniques we developed are based on Siegel's Lemma for the bounds, anti-concentration inequalities for the existential results and extensions of Sylvester-type Hadamard matrices for the constructions. We explicitly construct a constant weight, optimal size matrix to compute the EQUALITY function (checking if two integers expressed in binary are equal). Computing EQUALITY with a single linear equation requires exponentially large weights. In addition, we prove the existence of the best-known weight size (linear) matrices to compute the COMPARISON function (comparing between two integers expressed in binary). In the context of the circuit complexity theory, our results improve the upper bounds on the weight sizes for the best-known circuit sizes for EQUALITY and COMPARISON.

Expert Graphs: Synthesizing New Expertise via Collaboration

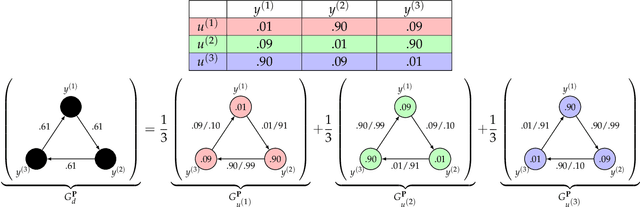
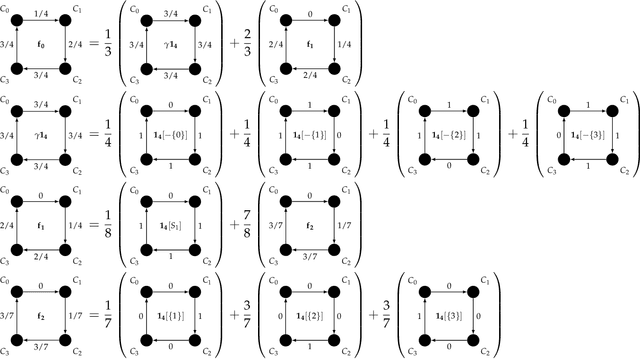
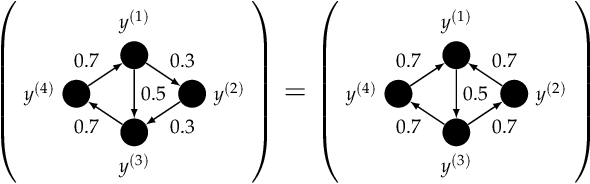
Consider multiple experts with overlapping expertise working on a classification problem under uncertain input. What constitutes a consistent set of opinions? How can we predict the opinions of experts on missing sub-domains? In this paper, we define a framework of to analyze this problem, termed "expert graphs." In an expert graph, vertices represent classes and edges represent binary opinions on the topics of their vertices. We derive necessary conditions for expert graph validity and use them to create "synthetic experts" which describe opinions consistent with the observed opinions of other experts. We show this framework to be equivalent to the well-studied linear ordering polytope. We show our conditions are not sufficient for describing all expert graphs on cliques, but are sufficient for cycles.

Robust Correction of Sampling Bias Using Cumulative Distribution Functions

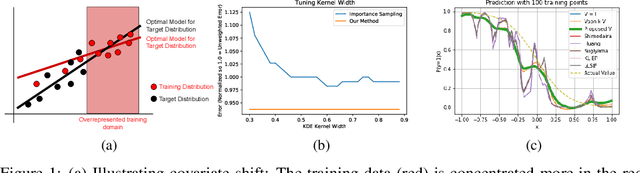
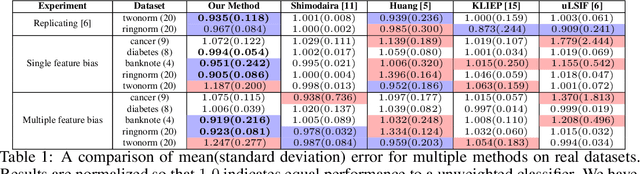
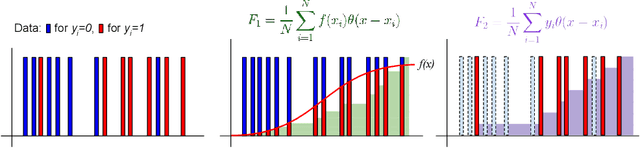
Varying domains and biased datasets can lead to differences between the training and the target distributions, known as covariate shift. Current approaches for alleviating this often rely on estimating the ratio of training and target probability density functions. These techniques require parameter tuning and can be unstable across different datasets. We present a new method for handling covariate shift using the empirical cumulative distribution function estimates of the target distribution by a rigorous generalization of a recent idea proposed by Vapnik and Izmailov. Further, we show experimentally that our method is more robust in its predictions, is not reliant on parameter tuning and shows similar classification performance compared to the current state-of-the-art techniques on synthetic and real datasets.

CodNN -- Robust Neural Networks From Coded Classification

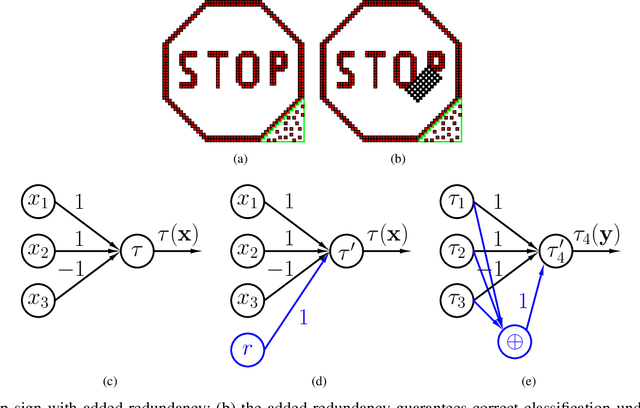
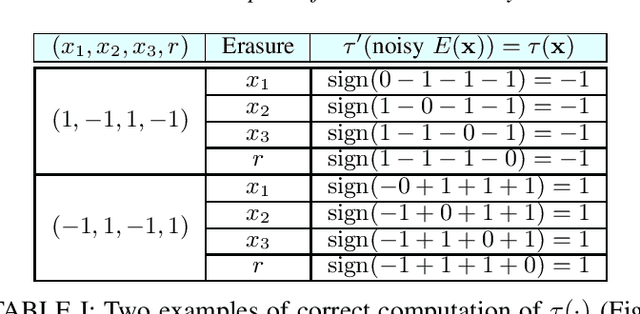
Deep Neural Networks (DNNs) are a revolutionary force in the ongoing information revolution, and yet their intrinsic properties remain a mystery. In particular, it is widely known that DNNs are highly sensitive to noise, whether adversarial or random. This poses a fundamental challenge for hardware implementations of DNNs, and for their deployment in critical applications such as autonomous driving. In this paper we construct robust DNNs via error correcting codes. By our approach, either the data or internal layers of the DNN are coded with error correcting codes, and successful computation under noise is guaranteed. Since DNNs can be seen as a layered concatenation of classification tasks, our research begins with the core task of classifying noisy coded inputs, and progresses towards robust DNNs. We focus on binary data and linear codes. Our main result is that the prevalent parity code can guarantee robustness for a large family of DNNs, which includes the recently popularized binarized neural networks. Further, we show that the coded classification problem has a deep connection to Fourier analysis of Boolean functions. In contrast to existing solutions in the literature, our results do not rely on altering the training process of the DNN, and provide mathematically rigorous guarantees rather than experimental evidence.

What is the Value of Data? On Mathematical Methods for Data Quality Estimation

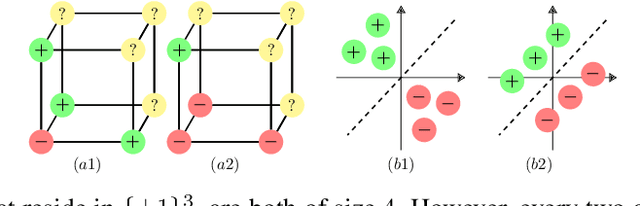
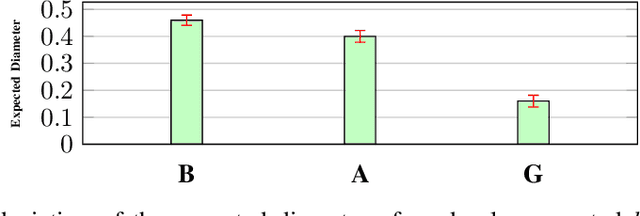
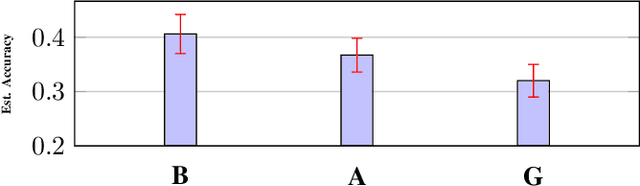
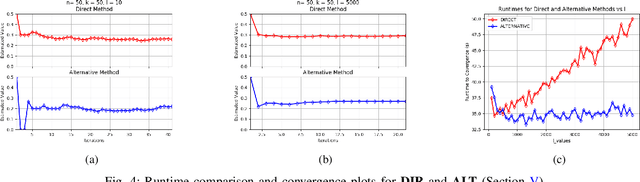
Data is one of the most important assets of the information age, and its societal impact is undisputed. Yet, rigorous methods of assessing the quality of data are lacking. In this paper, we propose a formal definition for the quality of a given dataset. We assess a dataset's quality by a quantity we call the expected diameter, which measures the expected disagreement between two randomly chosen hypotheses that explain it, and has recently found applications in active learning. We focus on Boolean hyperplanes, and utilize a collection of Fourier analytic, algebraic, and probabilistic methods to come up with theoretical guarantees and practical solutions for the computation of the expected diameter. We also study the behaviour of the expected diameter on algebraically structured datasets, conduct experiments that validate this notion of quality, and demonstrate the feasibility of our techniques.

The Capacity of String-Replication Systems

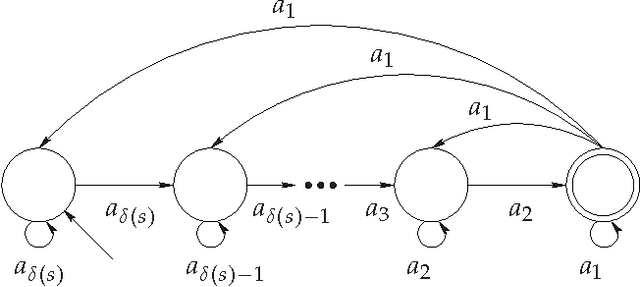
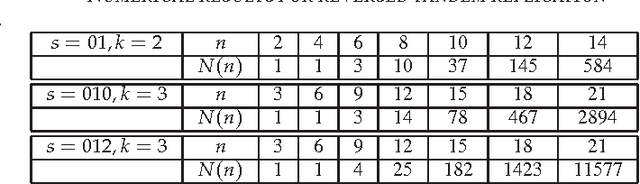
It is known that the majority of the human genome consists of repeated sequences. Furthermore, it is believed that a significant part of the rest of the genome also originated from repeated sequences and has mutated to its current form. In this paper, we investigate the possibility of constructing an exponentially large number of sequences from a short initial sequence and simple replication rules, including those resembling genomic replication processes. In other words, our goal is to find out the capacity, or the expressive power, of these string-replication systems. Our results include exact capacities, and bounds on the capacities, of four fundamental string-replication systems.