CodNN -- Robust Neural Networks From Coded Classification
Paper and Code
Apr 29, 2020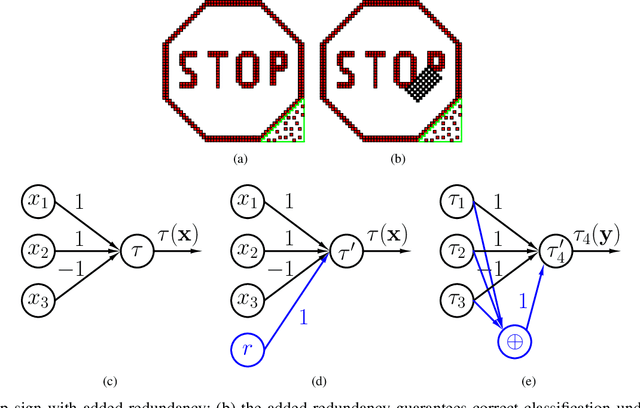
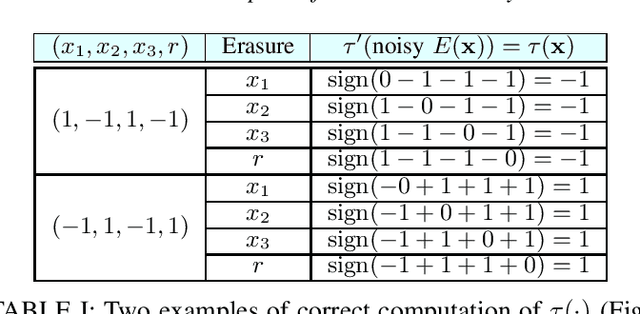
Deep Neural Networks (DNNs) are a revolutionary force in the ongoing information revolution, and yet their intrinsic properties remain a mystery. In particular, it is widely known that DNNs are highly sensitive to noise, whether adversarial or random. This poses a fundamental challenge for hardware implementations of DNNs, and for their deployment in critical applications such as autonomous driving. In this paper we construct robust DNNs via error correcting codes. By our approach, either the data or internal layers of the DNN are coded with error correcting codes, and successful computation under noise is guaranteed. Since DNNs can be seen as a layered concatenation of classification tasks, our research begins with the core task of classifying noisy coded inputs, and progresses towards robust DNNs. We focus on binary data and linear codes. Our main result is that the prevalent parity code can guarantee robustness for a large family of DNNs, which includes the recently popularized binarized neural networks. Further, we show that the coded classification problem has a deep connection to Fourier analysis of Boolean functions. In contrast to existing solutions in the literature, our results do not rely on altering the training process of the DNN, and provide mathematically rigorous guarantees rather than experimental evidence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge