Anxiao Jiang
CODA: Temporal Domain Generalization via Concept Drift Simulator
Oct 02, 2023Abstract:In real-world applications, machine learning models often become obsolete due to shifts in the joint distribution arising from underlying temporal trends, a phenomenon known as the "concept drift". Existing works propose model-specific strategies to achieve temporal generalization in the near-future domain. However, the diverse characteristics of real-world datasets necessitate customized prediction model architectures. To this end, there is an urgent demand for a model-agnostic temporal domain generalization approach that maintains generality across diverse data modalities and architectures. In this work, we aim to address the concept drift problem from a data-centric perspective to bypass considering the interaction between data and model. Developing such a framework presents non-trivial challenges: (i) existing generative models struggle to generate out-of-distribution future data, and (ii) precisely capturing the temporal trends of joint distribution along chronological source domains is computationally infeasible. To tackle the challenges, we propose the COncept Drift simulAtor (CODA) framework incorporating a predicted feature correlation matrix to simulate future data for model training. Specifically, CODA leverages feature correlations to represent data characteristics at specific time points, thereby circumventing the daunting computational costs. Experimental results demonstrate that using CODA-generated data as training input effectively achieves temporal domain generalization across different model architectures.
CodNN -- Robust Neural Networks From Coded Classification
Apr 29, 2020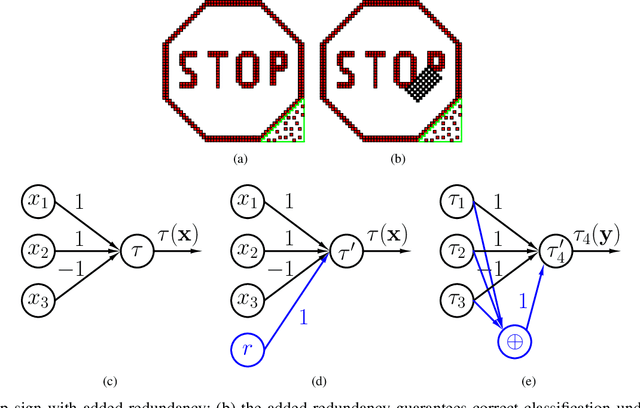
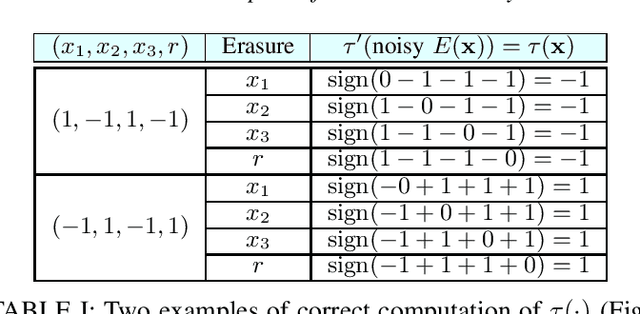
Abstract:Deep Neural Networks (DNNs) are a revolutionary force in the ongoing information revolution, and yet their intrinsic properties remain a mystery. In particular, it is widely known that DNNs are highly sensitive to noise, whether adversarial or random. This poses a fundamental challenge for hardware implementations of DNNs, and for their deployment in critical applications such as autonomous driving. In this paper we construct robust DNNs via error correcting codes. By our approach, either the data or internal layers of the DNN are coded with error correcting codes, and successful computation under noise is guaranteed. Since DNNs can be seen as a layered concatenation of classification tasks, our research begins with the core task of classifying noisy coded inputs, and progresses towards robust DNNs. We focus on binary data and linear codes. Our main result is that the prevalent parity code can guarantee robustness for a large family of DNNs, which includes the recently popularized binarized neural networks. Further, we show that the coded classification problem has a deep connection to Fourier analysis of Boolean functions. In contrast to existing solutions in the literature, our results do not rely on altering the training process of the DNN, and provide mathematically rigorous guarantees rather than experimental evidence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge