Linear Codes for Hyperdimensional Computing

Hyperdimensional Computing (HDC) is an emerging computational paradigm for representing compositional information as high-dimensional vectors, and has a promising potential in applications ranging from machine learning to neuromorphic computing. One of the long-standing challenges in HDC is factoring a compositional representation to its constituent factors, also known as the recovery problem. In this paper we take a novel approach to solve the recovery problem, and propose the use of random linear codes. These codes are subspaces over the Boolean field, and are a well-studied topic in information theory with various applications in digital communication. We begin by showing that hyperdimensional encoding using random linear codes retains favorable properties of the prevalent (ordinary) random codes, and hence HD representations using the two methods have comparable information storage capabilities. We proceed to show that random linear codes offer a rich subcode structure that can be used to form key-value stores, which encapsulate most use cases of HDC. Most importantly, we show that under the framework we develop, random linear codes admit simple recovery algorithms to factor (either bundled or bound) compositional representations. The former relies on constructing certain linear equation systems over the Boolean field, the solution to which reduces the search space dramatically and strictly outperforms exhaustive search in many cases. The latter employs the subspace structure of these codes to achieve provably correct factorization. Both methods are strictly faster than the state-of-the-art resonator networks, often by an order of magnitude. We implemented our techniques in Python using a benchmark software library, and demonstrated promising experimental results.

Beyond PCA: A Probabilistic Gram-Schmidt Approach to Feature Extraction

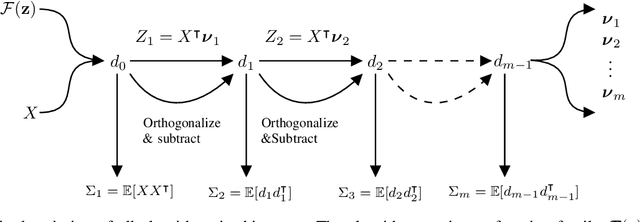
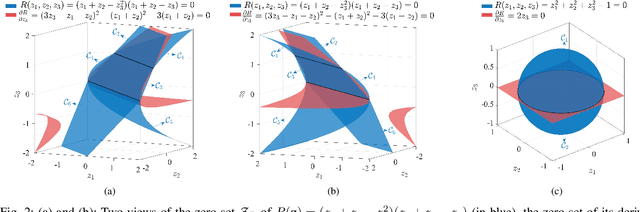
Linear feature extraction at the presence of nonlinear dependencies among the data is a fundamental challenge in unsupervised learning. We propose using a Probabilistic Gram-Schmidt (PGS) type orthogonalization process in order to detect and map out redundant dimensions. Specifically, by applying the PGS process over any family of functions which presumably captures the nonlinear dependencies in the data, we construct a series of covariance matrices that can either be used to remove those dependencies from the principal components, or to identify new large-variance directions. In the former case, we prove that under certain assumptions the resulting algorithms detect and remove nonlinear dependencies whenever those dependencies lie in the linear span of the chosen function family. In the latter, we provide information-theoretic guarantees in terms of entropy reduction. Both proposed methods extract linear features from the data while removing nonlinear redundancies. We provide simulation results on synthetic and real-world datasets which show improved performance over PCA and state-of-the-art linear feature extraction algorithms, both in terms of variance maximization of the extracted features, and in terms of improved performance of classification algorithms.

Enhancing Robustness of Neural Networks through Fourier Stabilization

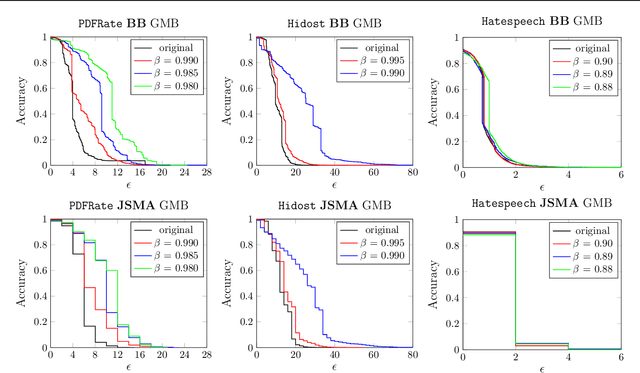
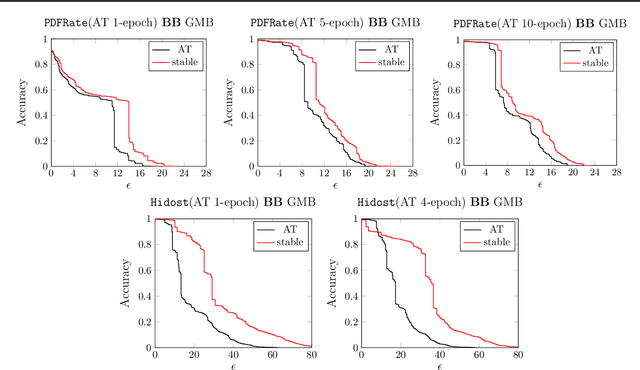
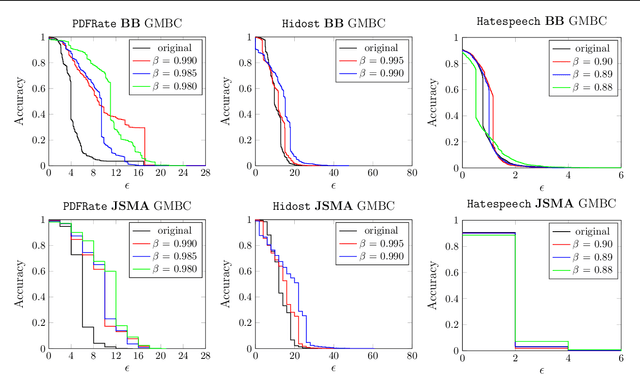
Despite the considerable success of neural networks in security settings such as malware detection, such models have proved vulnerable to evasion attacks, in which attackers make slight changes to inputs (e.g., malware) to bypass detection. We propose a novel approach, \emph{Fourier stabilization}, for designing evasion-robust neural networks with binary inputs. This approach, which is complementary to other forms of defense, replaces the weights of individual neurons with robust analogs derived using Fourier analytic tools. The choice of which neurons to stabilize in a neural network is then a combinatorial optimization problem, and we propose several methods for approximately solving it. We provide a formal bound on the per-neuron drop in accuracy due to Fourier stabilization, and experimentally demonstrate the effectiveness of the proposed approach in boosting robustness of neural networks in several detection settings. Moreover, we show that our approach effectively composes with adversarial training.

CodNN -- Robust Neural Networks From Coded Classification

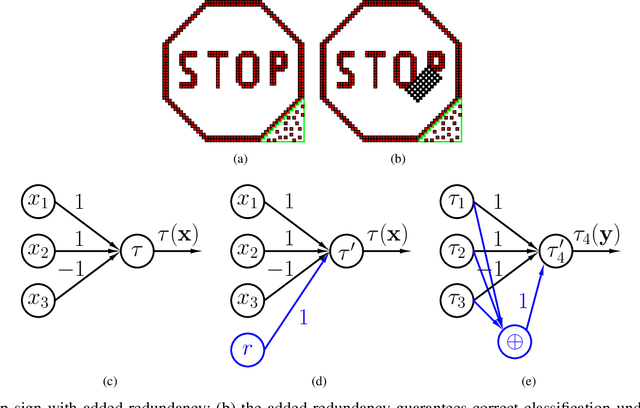
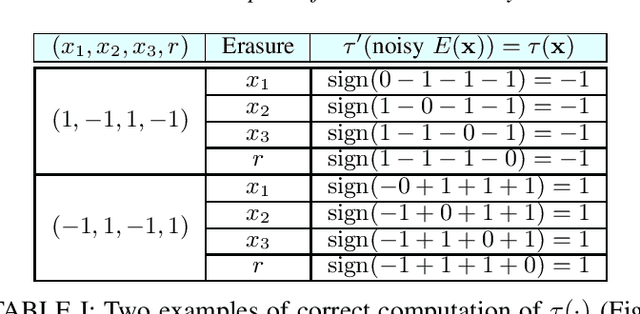
Deep Neural Networks (DNNs) are a revolutionary force in the ongoing information revolution, and yet their intrinsic properties remain a mystery. In particular, it is widely known that DNNs are highly sensitive to noise, whether adversarial or random. This poses a fundamental challenge for hardware implementations of DNNs, and for their deployment in critical applications such as autonomous driving. In this paper we construct robust DNNs via error correcting codes. By our approach, either the data or internal layers of the DNN are coded with error correcting codes, and successful computation under noise is guaranteed. Since DNNs can be seen as a layered concatenation of classification tasks, our research begins with the core task of classifying noisy coded inputs, and progresses towards robust DNNs. We focus on binary data and linear codes. Our main result is that the prevalent parity code can guarantee robustness for a large family of DNNs, which includes the recently popularized binarized neural networks. Further, we show that the coded classification problem has a deep connection to Fourier analysis of Boolean functions. In contrast to existing solutions in the literature, our results do not rely on altering the training process of the DNN, and provide mathematically rigorous guarantees rather than experimental evidence.

What is the Value of Data? On Mathematical Methods for Data Quality Estimation

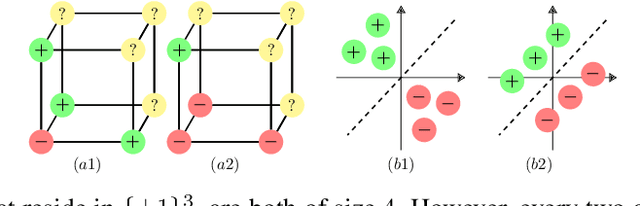
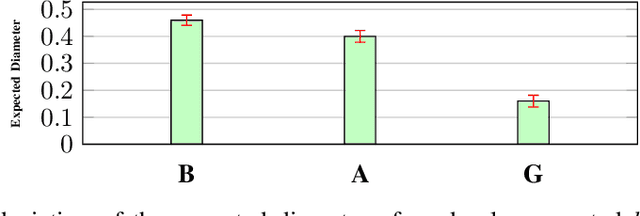
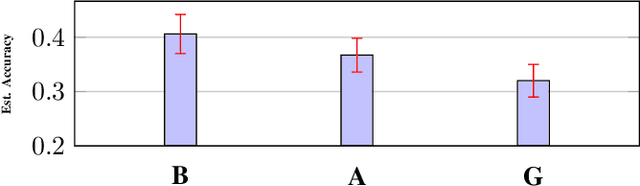
Data is one of the most important assets of the information age, and its societal impact is undisputed. Yet, rigorous methods of assessing the quality of data are lacking. In this paper, we propose a formal definition for the quality of a given dataset. We assess a dataset's quality by a quantity we call the expected diameter, which measures the expected disagreement between two randomly chosen hypotheses that explain it, and has recently found applications in active learning. We focus on Boolean hyperplanes, and utilize a collection of Fourier analytic, algebraic, and probabilistic methods to come up with theoretical guarantees and practical solutions for the computation of the expected diameter. We also study the behaviour of the expected diameter on algebraically structured datasets, conduct experiments that validate this notion of quality, and demonstrate the feasibility of our techniques.

Gradient Coding from Cyclic MDS Codes and Expander Graphs

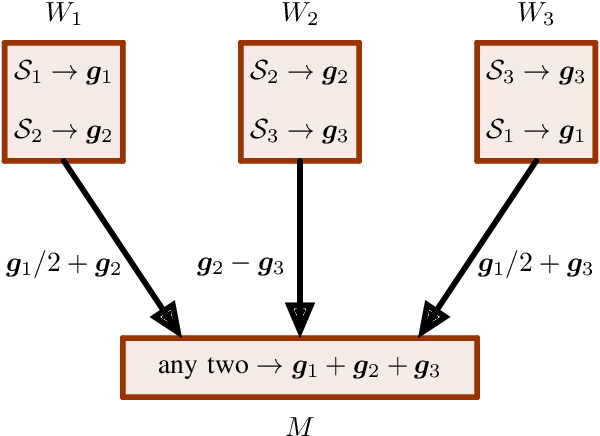
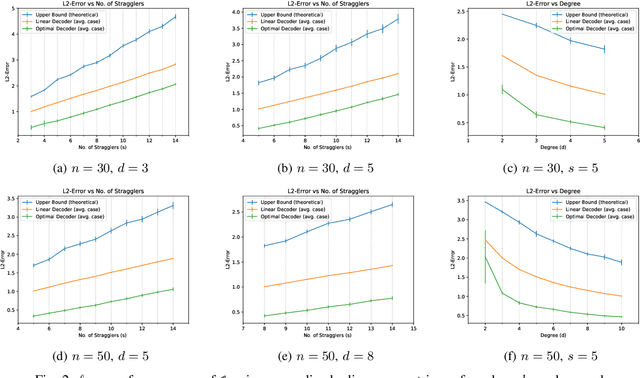
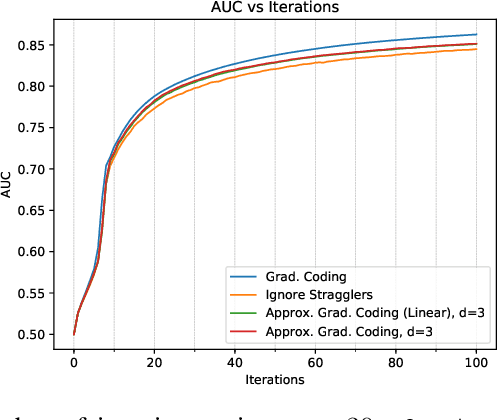
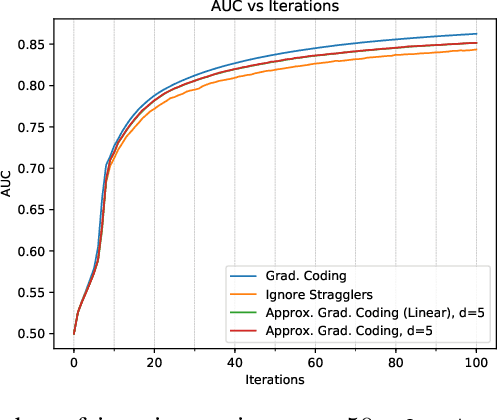
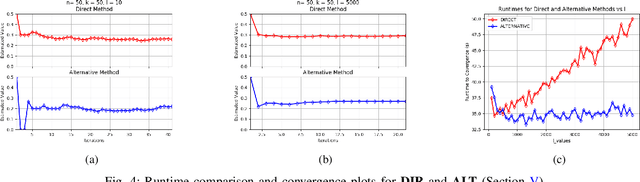
Gradient coding is a technique for straggler mitigation in distributed learning. In this paper we design novel gradient codes using tools from classical coding theory, namely, cyclic MDS codes, which compare favourably with existing solutions, both in the applicable range of parameters and in the complexity of the involved algorithms. Second, we introduce an approximate variant of the gradient coding problem, in which we settle for approximate gradient computation instead of the exact one. This approach enables graceful degradation, i.e., the $\ell_2$ error of the approximate gradient is a decreasing function of the number of stragglers. Our main result is that the normalized adjacency matrix of an expander graph can yield excellent approximate gradient codes, and that this approach allows us to perform significantly less computation compared to exact gradient coding. We experimentally test our approach on Amazon EC2, and show that the generalization error of approximate gradient coding is very close to the full gradient while requiring significantly less computation from the workers.

Lagrange Coded Computing: Optimal Design for Resiliency, Security and Privacy

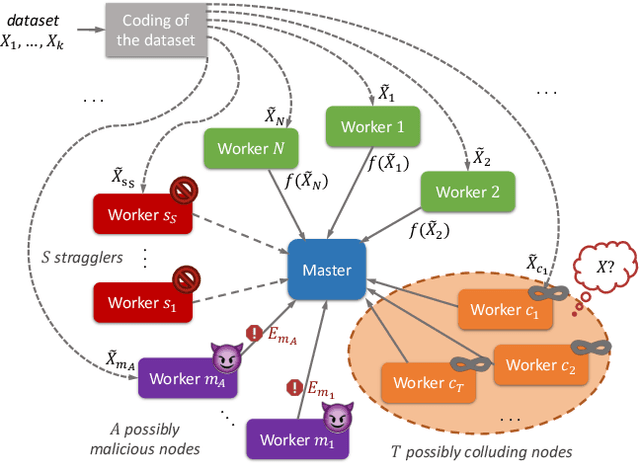
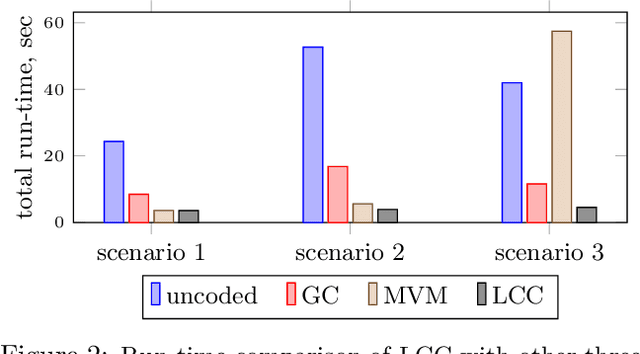
We consider a distributed computing scenario that involves computations over a massive dataset that is stored distributedly across multiple workers. We propose Lagrange Coded Computing, a new framework to simultaneously provide (1) resiliency against straggler workers that may prolong computations; (2) security against Byzantine (or malicious) workers that deliberately modify the computation for their benefit; and (3) (information-theoretic) privacy of the dataset amidst possible collusion of workers. Lagrange Coded Computing, which leverages the well-known Lagrange polynomial to create computation redundancy in a novel coded form across the workers, can be applied to any computation scenario in which the function of interest is an arbitrary multivariate polynomial of the input dataset, hence covering many computations of interest in machine learning. Lagrange Coded Computing significantly generalizes prior works to go beyond linear computations that have so far been the main focus in this area. We prove the optimality of Lagrange Coded Computing by developing matching converses, and empirically demonstrate its impact in mitigating stragglers and malicious workers.