Rashish Tandon
Gradient Coding from Cyclic MDS Codes and Expander Graphs
Sep 18, 2018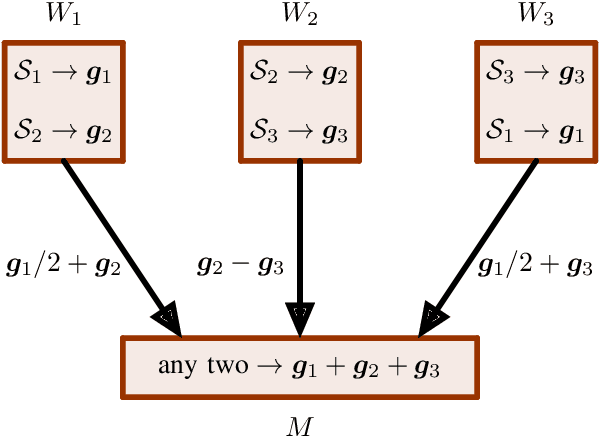
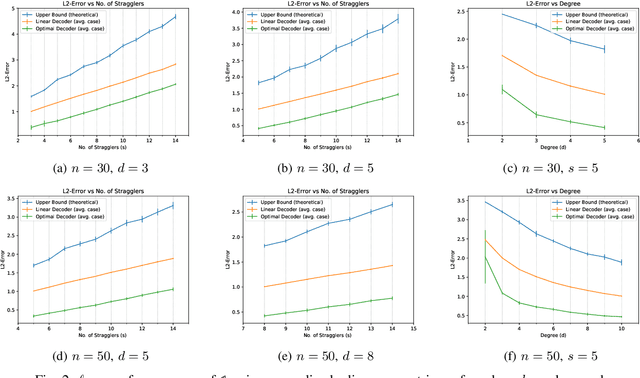
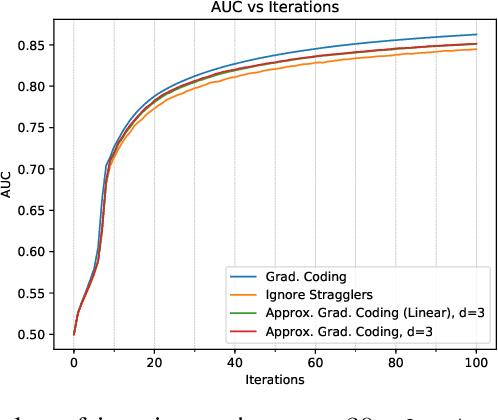
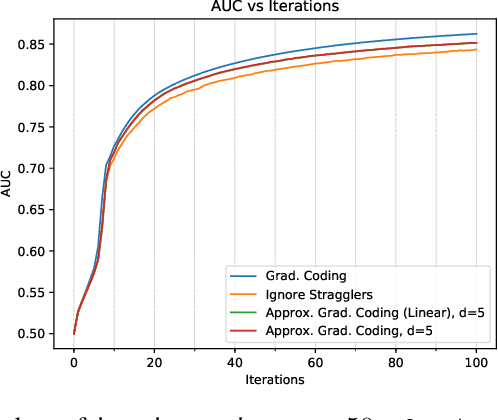
Abstract:Gradient coding is a technique for straggler mitigation in distributed learning. In this paper we design novel gradient codes using tools from classical coding theory, namely, cyclic MDS codes, which compare favourably with existing solutions, both in the applicable range of parameters and in the complexity of the involved algorithms. Second, we introduce an approximate variant of the gradient coding problem, in which we settle for approximate gradient computation instead of the exact one. This approach enables graceful degradation, i.e., the $\ell_2$ error of the approximate gradient is a decreasing function of the number of stragglers. Our main result is that the normalized adjacency matrix of an expander graph can yield excellent approximate gradient codes, and that this approach allows us to perform significantly less computation compared to exact gradient coding. We experimentally test our approach on Amazon EC2, and show that the generalization error of approximate gradient coding is very close to the full gradient while requiring significantly less computation from the workers.
Gradient Coding
Mar 08, 2017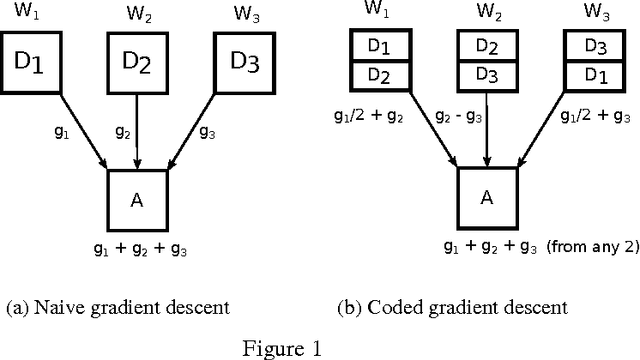
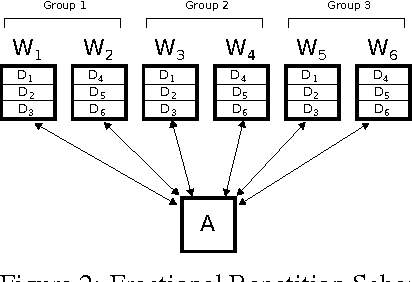
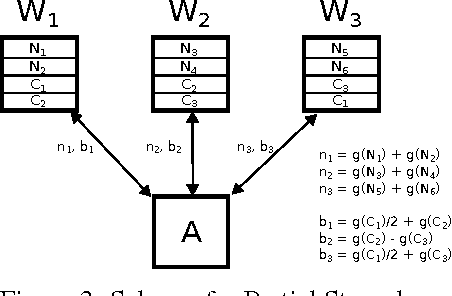
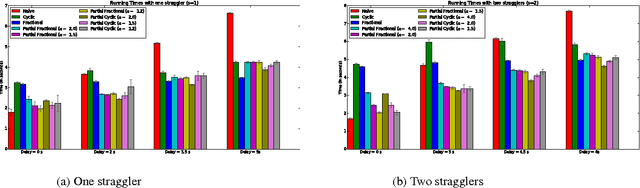
Abstract:We propose a novel coding theoretic framework for mitigating stragglers in distributed learning. We show how carefully replicating data blocks and coding across gradients can provide tolerance to failures and stragglers for Synchronous Gradient Descent. We implement our schemes in python (using MPI) to run on Amazon EC2, and show how we compare against baseline approaches in running time and generalization error.
Kernel Ridge Regression via Partitioning
Aug 05, 2016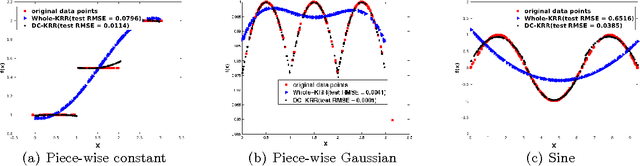
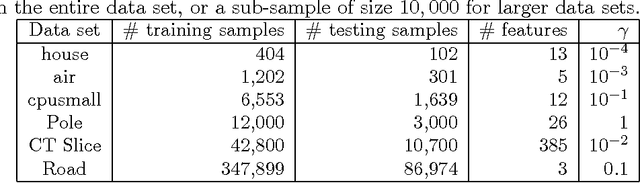
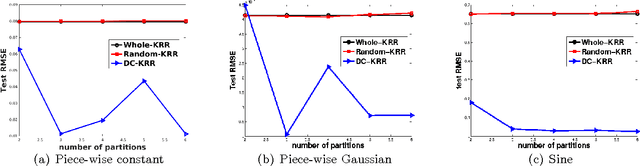

Abstract:In this paper, we investigate a divide and conquer approach to Kernel Ridge Regression (KRR). Given n samples, the division step involves separating the points based on some underlying disjoint partition of the input space (possibly via clustering), and then computing a KRR estimate for each partition. The conquering step is simple: for each partition, we only consider its own local estimate for prediction. We establish conditions under which we can give generalization bounds for this estimator, as well as achieve optimal minimax rates. We also show that the approximation error component of the generalization error is lesser than when a single KRR estimate is fit on the data: thus providing both statistical and computational advantages over a single KRR estimate over the entire data (or an averaging over random partitions as in other recent work, [30]). Lastly, we provide experimental validation for our proposed estimator and our assumptions.
On the Information Theoretic Limits of Learning Ising Models
Dec 05, 2014Abstract:We provide a general framework for computing lower-bounds on the sample complexity of recovering the underlying graphs of Ising models, given i.i.d samples. While there have been recent results for specific graph classes, these involve fairly extensive technical arguments that are specialized to each specific graph class. In contrast, we isolate two key graph-structural ingredients that can then be used to specify sample complexity lower-bounds. Presence of these structural properties makes the graph class hard to learn. We derive corollaries of our main result that not only recover existing recent results, but also provide lower bounds for novel graph classes not considered previously. We also extend our framework to the random graph setting and derive corollaries for Erd\H{o}s-R\'{e}nyi graphs in a certain dense setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge