Regret minimization in Linear Bandits with offline data via extended D-optimal exploration

We consider the problem of online regret minimization in linear bandits with access to prior observations (offline data) from the underlying bandit model. There are numerous applications where extensive offline data is often available, such as in recommendation systems, online advertising. Consequently, this problem has been studied intensively in recent literature. Our algorithm, Offline-Online Phased Elimination (OOPE), effectively incorporates the offline data to substantially reduce the online regret compared to prior work. To leverage offline information prudently, OOPE uses an extended D-optimal design within each exploration phase. OOPE achieves an online regret is $\tilde{O}(\sqrt{\deff T \log \left(|\mathcal{A}|T\right)}+d^2)$. $\deff \leq d)$ is the effective problem dimension which measures the number of poorly explored directions in offline data and depends on the eigen-spectrum $(\lambda_k)_{k \in [d]}$ of the Gram matrix of the offline data. The eigen-spectrum $(\lambda_k)_{k \in [d]}$ is a quantitative measure of the \emph{quality} of offline data. If the offline data is poorly explored ($\deff \approx d$), we recover the established regret bounds for purely online setting while, when offline data is abundant ($\Toff >> T$) and well-explored ($\deff = o(1) $), the online regret reduces substantially. Additionally, we provide the first known minimax regret lower bounds in this setting that depend explicitly on the quality of the offline data. These lower bounds establish the optimality of our algorithm in regimes where offline data is either well-explored or poorly explored. Finally, by using a Frank-Wolfe approximation to the extended optimal design we further improve the $O(d^{2})$ term to $O\left(\frac{d^{2}}{\deff} \min \{ \deff,1\} \right)$, which can be substantial in high dimensions with moderate quality of offline data $\deff = \Omega(1)$.

Efficient Approximate Posterior Sampling with Annealed Langevin Monte Carlo

We study the problem of posterior sampling in the context of score based generative models. We have a trained score network for a prior $p(x)$, a measurement model $p(y|x)$, and are tasked with sampling from the posterior $p(x|y)$. Prior work has shown this to be intractable in KL (in the worst case) under well-accepted computational hardness assumptions. Despite this, popular algorithms for tasks such as image super-resolution, stylization, and reconstruction enjoy empirical success. Rather than establishing distributional assumptions or restricted settings under which exact posterior sampling is tractable, we view this as a more general "tilting" problem of biasing a distribution towards a measurement. Under minimal assumptions, we show that one can tractably sample from a distribution that is simultaneously close to the posterior of a noised prior in KL divergence and the true posterior in Fisher divergence. Intuitively, this combination ensures that the resulting sample is consistent with both the measurement and the prior. To the best of our knowledge these are the first formal results for (approximate) posterior sampling in polynomial time.

Path-specific effects for pulse-oximetry guided decisions in critical care

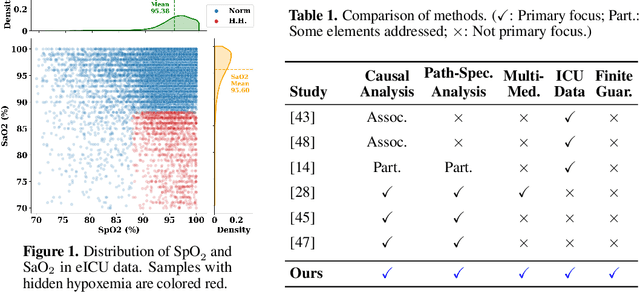
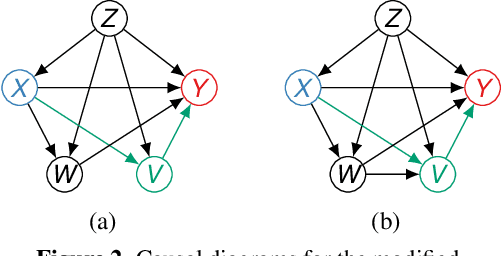
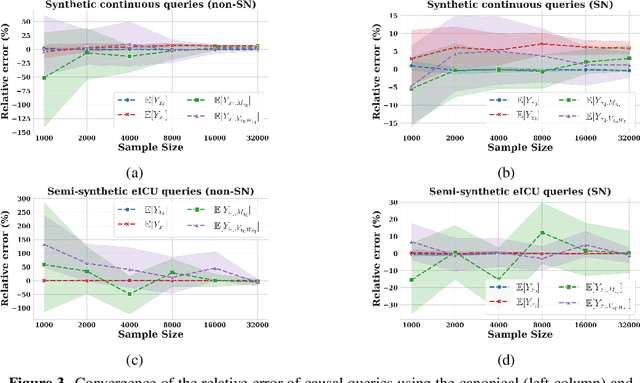
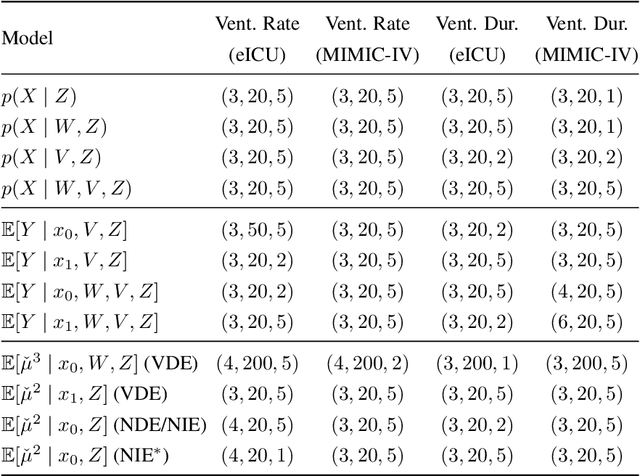
Identifying and measuring biases associated with sensitive attributes is a crucial consideration in healthcare to prevent treatment disparities. One prominent issue is inaccurate pulse oximeter readings, which tend to overestimate oxygen saturation for dark-skinned patients and misrepresent supplemental oxygen needs. Most existing research has revealed statistical disparities linking device errors to patient outcomes in intensive care units (ICUs) without causal formalization. In contrast, this study causally investigates how racial discrepancies in oximetry measurements affect invasive ventilation in ICU settings. We employ a causal inference-based approach using path-specific effects to isolate the impact of bias by race on clinical decision-making. To estimate these effects, we leverage a doubly robust estimator, propose its self-normalized variant for improved sample efficiency, and provide novel finite-sample guarantees. Our methodology is validated on semi-synthetic data and applied to two large real-world health datasets: MIMIC-IV and eICU. Contrary to prior work, our analysis reveals minimal impact of racial discrepancies on invasive ventilation rates. However, path-specific effects mediated by oxygen saturation disparity are more pronounced on ventilation duration, and the severity differs by dataset. Our work provides a novel and practical pipeline for investigating potential disparities in the ICU and, more crucially, highlights the necessity of causal methods to robustly assess fairness in decision-making.

Preference-centric Bandits: Optimality of Mixtures and Regret-efficient Algorithms

The objective of canonical multi-armed bandits is to identify and repeatedly select an arm with the largest reward, often in the form of the expected value of the arm's probability distribution. Such a utilitarian perspective and focus on the probability models' first moments, however, is agnostic to the distributions' tail behavior and their implications for variability and risks in decision-making. This paper introduces a principled framework for shifting from expectation-based evaluation to an alternative reward formulation, termed a preference metric (PM). The PMs can place the desired emphasis on different reward realization and can encode a richer modeling of preferences that incorporate risk aversion, robustness, or other desired attitudes toward uncertainty. A fundamentally distinct observation in such a PM-centric perspective is that designing bandit algorithms will have a significantly different principle: as opposed to the reward-based models in which the optimal sampling policy converges to repeatedly sampling from the single best arm, in the PM-centric framework the optimal policy converges to selecting a mix of arms based on specific mixing weights. Designing such mixture policies departs from the principles for designing bandit algorithms in significant ways, primarily because of uncountable mixture possibilities. The paper formalizes the PM-centric framework and presents two algorithm classes (horizon-dependent and anytime) that learn and track mixtures in a regret-efficient fashion. These algorithms have two distinctions from their canonical counterparts: (i) they involve an estimation routine to form reliable estimates of optimal mixtures, and (ii) they are equipped with tracking mechanisms to navigate arm selection fractions to track the optimal mixtures. These algorithms' regret guarantees are investigated under various algebraic forms of the PMs.

Representation Learning Preserving Ignorability and Covariate Matching for Treatment Effects

Estimating treatment effects from observational data is challenging due to two main reasons: (a) hidden confounding, and (b) covariate mismatch (control and treatment groups not having identical distributions). Long lines of works exist that address only either of these issues. To address the former, conventional techniques that require detailed knowledge in the form of causal graphs have been proposed. For the latter, covariate matching and importance weighting methods have been used. Recently, there has been progress in combining testable independencies with partial side information for tackling hidden confounding. A common framework to address both hidden confounding and selection bias is missing. We propose neural architectures that aim to learn a representation of pre-treatment covariates that is a valid adjustment and also satisfies covariate matching constraints. We combine two different neural architectures: one based on gradient matching across domains created by subsampling a suitable anchor variable that assumes causal side information, followed by the other, a covariate matching transformation. We prove that approximately invariant representations yield approximate valid adjustment sets which would enable an interval around the true causal effect. In contrast to usual sensitivity analysis, where an unknown nuisance parameter is varied, we have a testable approximation yielding a bound on the effect estimate. We also outperform various baselines with respect to ATE and PEHE errors on causal benchmarks that include IHDP, Jobs, Cattaneo, and an image-based Crowd Management dataset.

Risk-sensitive Bandits: Arm Mixture Optimality and Regret-efficient Algorithms

This paper introduces a general framework for risk-sensitive bandits that integrates the notions of risk-sensitive objectives by adopting a rich class of distortion riskmetrics. The introduced framework subsumes the various existing risk-sensitive models. An important and hitherto unknown observation is that for a wide range of riskmetrics, the optimal bandit policy involves selecting a mixture of arms. This is in sharp contrast to the convention in the multi-arm bandit algorithms that there is generally a solitary arm that maximizes the utility, whether purely reward-centric or risk-sensitive. This creates a major departure from the principles for designing bandit algorithms since there are uncountable mixture possibilities. The contributions of the paper are as follows: (i) it formalizes a general framework for risk-sensitive bandits, (ii) identifies standard risk-sensitive bandit models for which solitary arm selections is not optimal, (iii) and designs regret-efficient algorithms whose sampling strategies can accurately track optimal arm mixtures (when mixture is optimal) or the solitary arms (when solitary is optimal). The algorithms are shown to achieve a regret that scales according to $O((\log T/T )^{\nu})$, where $T$ is the horizon, and $\nu>0$ is a riskmetric-specific constant.

Online Bidding under RoS Constraints without Knowing the Value

We consider the problem of bidding in online advertising, where an advertiser aims to maximize value while adhering to budget and Return-on-Spend (RoS) constraints. Unlike prior work that assumes knowledge of the value generated by winning each impression ({e.g.,} conversions), we address the more realistic setting where the advertiser must simultaneously learn the optimal bidding strategy and the value of each impression opportunity. This introduces a challenging exploration-exploitation dilemma: the advertiser must balance exploring different bids to estimate impression values with exploiting current knowledge to bid effectively. To address this, we propose a novel Upper Confidence Bound (UCB)-style algorithm that carefully manages this trade-off. Via a rigorous theoretical analysis, we prove that our algorithm achieves $\widetilde{O}(\sqrt{T\log(|\mathcal{B}|T)})$ regret and constraint violation, where $T$ is the number of bidding rounds and $\mathcal{B}$ is the domain of possible bids. This establishes the first optimal regret and constraint violation bounds for bidding in the online setting with unknown impression values. Moreover, our algorithm is computationally efficient and simple to implement. We validate our theoretical findings through experiments on synthetic data, demonstrating that our algorithm exhibits strong empirical performance compared to existing approaches.

Interleaved Gibbs Diffusion for Constrained Generation

We introduce Interleaved Gibbs Diffusion (IGD), a novel generative modeling framework for mixed continuous-discrete data, focusing on constrained generation problems. Prior works on discrete and continuous-discrete diffusion models assume factorized denoising distribution for fast generation, which can hinder the modeling of strong dependencies between random variables encountered in constrained generation. IGD moves beyond this by interleaving continuous and discrete denoising algorithms via a discrete time Gibbs sampling type Markov chain. IGD provides flexibility in the choice of denoisers, allows conditional generation via state-space doubling and inference time scaling via the ReDeNoise method. Empirical evaluations on three challenging tasks-solving 3-SAT, generating molecule structures, and generating layouts-demonstrate state-of-the-art performance. Notably, IGD achieves a 7% improvement on 3-SAT out of the box and achieves state-of-the-art results in molecule generation without relying on equivariant diffusion or domain-specific architectures. We explore a wide range of modeling, and interleaving strategies along with hyperparameters in each of these problems.

Does Safety Training of LLMs Generalize to Semantically Related Natural Prompts?

Large Language Models (LLMs) are known to be susceptible to crafted adversarial attacks or jailbreaks that lead to the generation of objectionable content despite being aligned to human preferences using safety fine-tuning methods. While the large dimensionality of input token space makes it inevitable to find adversarial prompts that can jailbreak these models, we aim to evaluate whether safety fine-tuned LLMs are safe against natural prompts which are semantically related to toxic seed prompts that elicit safe responses after alignment. We surprisingly find that popular aligned LLMs such as GPT-4 can be compromised using naive prompts that are NOT even crafted with an objective of jailbreaking the model. Furthermore, we empirically show that given a seed prompt that elicits a toxic response from an unaligned model, one can systematically generate several semantically related natural prompts that can jailbreak aligned LLMs. Towards this, we propose a method of Response Guided Question Augmentation (ReG-QA) to evaluate the generalization of safety aligned LLMs to natural prompts, that first generates several toxic answers given a seed question using an unaligned LLM (Q to A), and further leverages an LLM to generate questions that are likely to produce these answers (A to Q). We interestingly find that safety fine-tuned LLMs such as GPT-4o are vulnerable to producing natural jailbreak questions from unsafe content (without denial) and can thus be used for the latter (A to Q) step. We obtain attack success rates that are comparable to/ better than leading adversarial attack methods on the JailbreakBench leaderboard, while being significantly more stable against defenses such as Smooth-LLM and Synonym Substitution, which are effective against existing all attacks on the leaderboard.

Time-Reversal Provides Unsupervised Feedback to LLMs

Large Language Models (LLMs) are typically trained to predict in the forward direction of time. However, recent works have shown that prompting these models to look back and critique their own generations can produce useful feedback. Motivated by this, we explore the question of whether LLMs can be empowered to think (predict and score) backwards to provide unsupervised feedback that complements forward LLMs. Towards this, we introduce Time Reversed Language Models (TRLMs), which can score and generate queries when conditioned on responses, effectively functioning in the reverse direction of time. Further, to effectively infer in the response to query direction, we pre-train and fine-tune a language model (TRLM-Ba) in the reverse token order from scratch. We show empirically (and theoretically in a stylized setting) that time-reversed models can indeed complement forward model predictions when used to score the query given response for re-ranking multiple forward generations. We obtain up to 5\% improvement on the widely used AlpacaEval Leaderboard over the competent baseline of best-of-N re-ranking using self log-perplexity scores. We further show that TRLM scoring outperforms conventional forward scoring of response given query, resulting in significant gains in applications such as citation generation and passage retrieval. We next leverage the generative ability of TRLM to augment or provide unsupervised feedback to input safety filters of LLMs, demonstrating a drastic reduction in false negative rate with negligible impact on false positive rates against several attacks published on the popular JailbreakBench leaderboard.