Preference-centric Bandits: Optimality of Mixtures and Regret-efficient Algorithms

The objective of canonical multi-armed bandits is to identify and repeatedly select an arm with the largest reward, often in the form of the expected value of the arm's probability distribution. Such a utilitarian perspective and focus on the probability models' first moments, however, is agnostic to the distributions' tail behavior and their implications for variability and risks in decision-making. This paper introduces a principled framework for shifting from expectation-based evaluation to an alternative reward formulation, termed a preference metric (PM). The PMs can place the desired emphasis on different reward realization and can encode a richer modeling of preferences that incorporate risk aversion, robustness, or other desired attitudes toward uncertainty. A fundamentally distinct observation in such a PM-centric perspective is that designing bandit algorithms will have a significantly different principle: as opposed to the reward-based models in which the optimal sampling policy converges to repeatedly sampling from the single best arm, in the PM-centric framework the optimal policy converges to selecting a mix of arms based on specific mixing weights. Designing such mixture policies departs from the principles for designing bandit algorithms in significant ways, primarily because of uncountable mixture possibilities. The paper formalizes the PM-centric framework and presents two algorithm classes (horizon-dependent and anytime) that learn and track mixtures in a regret-efficient fashion. These algorithms have two distinctions from their canonical counterparts: (i) they involve an estimation routine to form reliable estimates of optimal mixtures, and (ii) they are equipped with tracking mechanisms to navigate arm selection fractions to track the optimal mixtures. These algorithms' regret guarantees are investigated under various algebraic forms of the PMs.

Real-Time Risky Fault-Chain Search using Time-Varying Graph RNNs

This paper introduces a data-driven graphical framework for the real-time search of risky cascading fault chains (FCs) in power-grids, crucial for enhancing grid resiliency in the face of climate change. As extreme weather events driven by climate change increase, identifying risky FCs becomes crucial for mitigating cascading failures and ensuring grid stability. However, the complexity of the spatio-temporal dependencies among grid components and the exponential growth of the search space with system size pose significant challenges to modeling and risky FC search. To tackle this, we model the search process as a partially observable Markov decision process (POMDP), which is subsequently solved via a time-varying graph recurrent neural network (GRNN). This approach captures the spatial and temporal structure induced by the system's topology and dynamics, while efficiently summarizing the system's history in the GRNN's latent space, enabling scalable and effective identification of risky FCs.

Risk-sensitive Bandits: Arm Mixture Optimality and Regret-efficient Algorithms

This paper introduces a general framework for risk-sensitive bandits that integrates the notions of risk-sensitive objectives by adopting a rich class of distortion riskmetrics. The introduced framework subsumes the various existing risk-sensitive models. An important and hitherto unknown observation is that for a wide range of riskmetrics, the optimal bandit policy involves selecting a mixture of arms. This is in sharp contrast to the convention in the multi-arm bandit algorithms that there is generally a solitary arm that maximizes the utility, whether purely reward-centric or risk-sensitive. This creates a major departure from the principles for designing bandit algorithms since there are uncountable mixture possibilities. The contributions of the paper are as follows: (i) it formalizes a general framework for risk-sensitive bandits, (ii) identifies standard risk-sensitive bandit models for which solitary arm selections is not optimal, (iii) and designs regret-efficient algorithms whose sampling strategies can accurately track optimal arm mixtures (when mixture is optimal) or the solitary arms (when solitary is optimal). The algorithms are shown to achieve a regret that scales according to $O((\log T/T )^{\nu})$, where $T$ is the horizon, and $\nu>0$ is a riskmetric-specific constant.

RL for Mitigating Cascading Failures: Targeted Exploration via Sensitivity Factors

Electricity grid's resiliency and climate change strongly impact one another due to an array of technical and policy-related decisions that impact both. This paper introduces a physics-informed machine learning-based framework to enhance grid's resiliency. Specifically, when encountering disruptive events, this paper designs remedial control actions to prevent blackouts. The proposed Physics-Guided Reinforcement Learning (PG-RL) framework determines effective real-time remedial line-switching actions, considering their impact on power balance, system security, and grid reliability. To identify an effective blackout mitigation policy, PG-RL leverages power-flow sensitivity factors to guide the RL exploration during agent training. Comprehensive evaluations using the Grid2Op platform demonstrate that incorporating physical signals into RL significantly improves resource utilization within electric grids and achieves better blackout mitigation policies - both of which are critical in addressing climate change.

Linear Causal Bandits: Unknown Graph and Soft Interventions

Designing causal bandit algorithms depends on two central categories of assumptions: (i) the extent of information about the underlying causal graphs and (ii) the extent of information about interventional statistical models. There have been extensive recent advances in dispensing with assumptions on either category. These include assuming known graphs but unknown interventional distributions, and the converse setting of assuming unknown graphs but access to restrictive hard/$\operatorname{do}$ interventions, which removes the stochasticity and ancestral dependencies. Nevertheless, the problem in its general form, i.e., unknown graph and unknown stochastic intervention models, remains open. This paper addresses this problem and establishes that in a graph with $N$ nodes, maximum in-degree $d$ and maximum causal path length $L$, after $T$ interaction rounds the regret upper bound scales as $\tilde{\mathcal{O}}((cd)^{L-\frac{1}{2}}\sqrt{T} + d + RN)$ where $c>1$ is a constant and $R$ is a measure of intervention power. A universal minimax lower bound is also established, which scales as $\Omega(d^{L-\frac{3}{2}}\sqrt{T})$. Importantly, the graph size $N$ has a diminishing effect on the regret as $T$ grows. These bounds have matching behavior in $T$, exponential dependence on $L$, and polynomial dependence on $d$ (with the gap $d\ $). On the algorithmic aspect, the paper presents a novel way of designing a computationally efficient CB algorithm, addressing a challenge that the existing CB algorithms using soft interventions face.

Cascading Failure Prediction via Causal Inference

Causal inference provides an analytical framework to identify and quantify cause-and-effect relationships among a network of interacting agents. This paper offers a novel framework for analyzing cascading failures in power transmission networks. This framework generates a directed latent graph in which the nodes represent the transmission lines and the directed edges encode the cause-effect relationships. This graph has a structure distinct from the system's topology, signifying the intricate fact that both local and non-local interdependencies exist among transmission lines, which are more general than only the local interdependencies that topological graphs can present. This paper formalizes a causal inference framework for predicting how an emerging anomaly propagates throughout the system. Using this framework, two algorithms are designed, providing an analytical framework to identify the most likely and most costly cascading scenarios. The framework's effectiveness is evaluated compared to the pertinent literature on the IEEE 14-bus, 39-bus, and 118-bus systems.

Combinatorial Multi-armed Bandits: Arm Selection via Group Testing

This paper considers the problem of combinatorial multi-armed bandits with semi-bandit feedback and a cardinality constraint on the super-arm size. Existing algorithms for solving this problem typically involve two key sub-routines: (1) a parameter estimation routine that sequentially estimates a set of base-arm parameters, and (2) a super-arm selection policy for selecting a subset of base arms deemed optimal based on these parameters. State-of-the-art algorithms assume access to an exact oracle for super-arm selection with unbounded computational power. At each instance, this oracle evaluates a list of score functions, the number of which grows as low as linearly and as high as exponentially with the number of arms. This can be prohibitive in the regime of a large number of arms. This paper introduces a novel realistic alternative to the perfect oracle. This algorithm uses a combination of group-testing for selecting the super arms and quantized Thompson sampling for parameter estimation. Under a general separability assumption on the reward function, the proposed algorithm reduces the complexity of the super-arm-selection oracle to be logarithmic in the number of base arms while achieving the same regret order as the state-of-the-art algorithms that use exact oracles. This translates to at least an exponential reduction in complexity compared to the oracle-based approaches.

Interventional Causal Discovery in a Mixture of DAGs

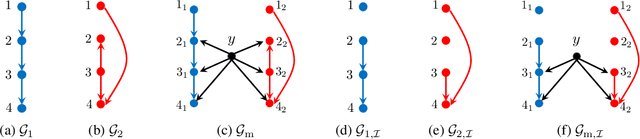
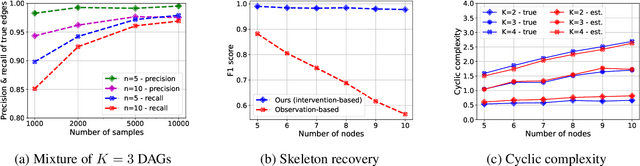
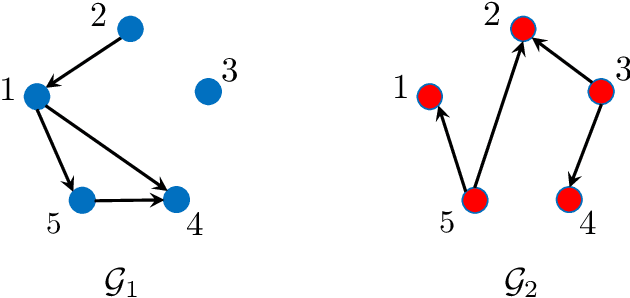
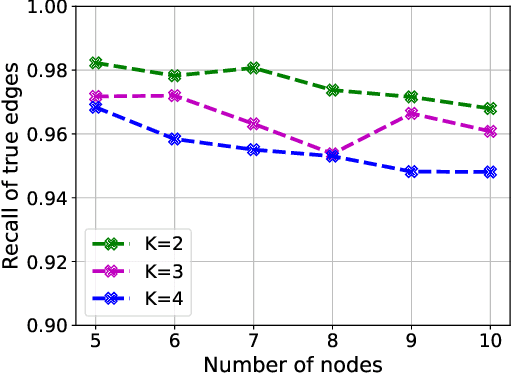
Causal interactions among a group of variables are often modeled by a single causal graph. In some domains, however, these interactions are best described by multiple co-existing causal graphs, e.g., in dynamical systems or genomics. This paper addresses the hitherto unknown role of interventions in learning causal interactions among variables governed by a mixture of causal systems, each modeled by one directed acyclic graph (DAG). Causal discovery from mixtures is fundamentally more challenging than single-DAG causal discovery. Two major difficulties stem from (i) inherent uncertainty about the skeletons of the component DAGs that constitute the mixture and (ii) possibly cyclic relationships across these component DAGs. This paper addresses these challenges and aims to identify edges that exist in at least one component DAG of the mixture, referred to as true edges. First, it establishes matching necessary and sufficient conditions on the size of interventions required to identify the true edges. Next, guided by the necessity results, an adaptive algorithm is designed that learns all true edges using ${\cal O}(n^2)$ interventions, where $n$ is the number of nodes. Remarkably, the size of the interventions is optimal if the underlying mixture model does not contain cycles across its components. More generally, the gap between the intervention size used by the algorithm and the optimal size is quantified. It is shown to be bounded by the cyclic complexity number of the mixture model, defined as the size of the minimal intervention that can break the cycles in the mixture, which is upper bounded by the number of cycles among the ancestors of a node.

Linear Causal Representation Learning from Unknown Multi-node Interventions

Despite the multifaceted recent advances in interventional causal representation learning (CRL), they primarily focus on the stylized assumption of single-node interventions. This assumption is not valid in a wide range of applications, and generally, the subset of nodes intervened in an interventional environment is fully unknown. This paper focuses on interventional CRL under unknown multi-node (UMN) interventional environments and establishes the first identifiability results for general latent causal models (parametric or nonparametric) under stochastic interventions (soft or hard) and linear transformation from the latent to observed space. Specifically, it is established that given sufficiently diverse interventional environments, (i) identifiability up to ancestors is possible using only soft interventions, and (ii) perfect identifiability is possible using hard interventions. Remarkably, these guarantees match the best-known results for more restrictive single-node interventions. Furthermore, CRL algorithms are also provided that achieve the identifiability guarantees. A central step in designing these algorithms is establishing the relationships between UMN interventional CRL and score functions associated with the statistical models of different interventional environments. Establishing these relationships also serves as constructive proof of the identifiability guarantees.

Improved Bound for Robust Causal Bandits with Linear Models

This paper investigates the robustness of causal bandits (CBs) in the face of temporal model fluctuations. This setting deviates from the existing literature's widely-adopted assumption of constant causal models. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown and subject to variations over time. The goal is to design a sequence of interventions that incur the smallest cumulative regret compared to an oracle aware of the entire causal model and its fluctuations. A robust CB algorithm is proposed, and its cumulative regret is analyzed by establishing both upper and lower bounds on the regret. It is shown that in a graph with maximum in-degree $d$, length of the largest causal path $L$, and an aggregate model deviation $C$, the regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{T} + C))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T}\; ,\; d^2C\})$. The proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$, maintaining sub-linear regret for a broad range of $C$.