Interventional Causal Discovery in a Mixture of DAGs

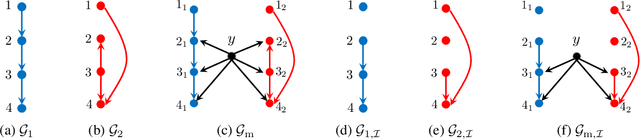
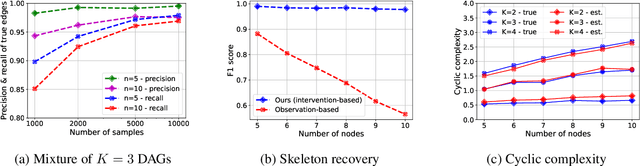
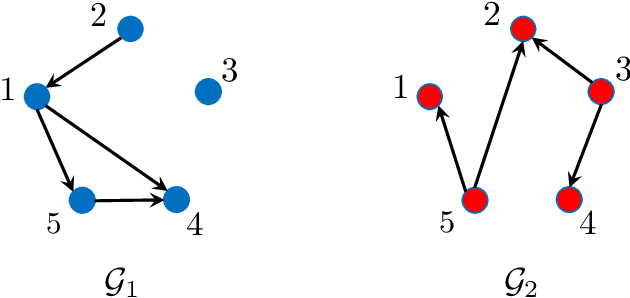
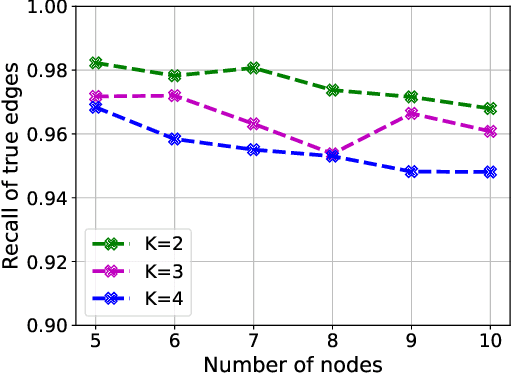
Causal interactions among a group of variables are often modeled by a single causal graph. In some domains, however, these interactions are best described by multiple co-existing causal graphs, e.g., in dynamical systems or genomics. This paper addresses the hitherto unknown role of interventions in learning causal interactions among variables governed by a mixture of causal systems, each modeled by one directed acyclic graph (DAG). Causal discovery from mixtures is fundamentally more challenging than single-DAG causal discovery. Two major difficulties stem from (i) inherent uncertainty about the skeletons of the component DAGs that constitute the mixture and (ii) possibly cyclic relationships across these component DAGs. This paper addresses these challenges and aims to identify edges that exist in at least one component DAG of the mixture, referred to as true edges. First, it establishes matching necessary and sufficient conditions on the size of interventions required to identify the true edges. Next, guided by the necessity results, an adaptive algorithm is designed that learns all true edges using ${\cal O}(n^2)$ interventions, where $n$ is the number of nodes. Remarkably, the size of the interventions is optimal if the underlying mixture model does not contain cycles across its components. More generally, the gap between the intervention size used by the algorithm and the optimal size is quantified. It is shown to be bounded by the cyclic complexity number of the mixture model, defined as the size of the minimal intervention that can break the cycles in the mixture, which is upper bounded by the number of cycles among the ancestors of a node.

Causal Bandits with General Causal Models and Interventions

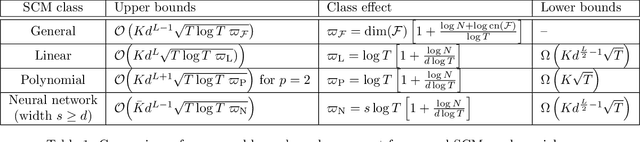
This paper considers causal bandits (CBs) for the sequential design of interventions in a causal system. The objective is to optimize a reward function via minimizing a measure of cumulative regret with respect to the best sequence of interventions in hindsight. The paper advances the results on CBs in three directions. First, the structural causal models (SCMs) are assumed to be unknown and drawn arbitrarily from a general class $\mathcal{F}$ of Lipschitz-continuous functions. Existing results are often focused on (generalized) linear SCMs. Second, the interventions are assumed to be generalized soft with any desired level of granularity, resulting in an infinite number of possible interventions. The existing literature, in contrast, generally adopts atomic and hard interventions. Third, we provide general upper and lower bounds on regret. The upper bounds subsume (and improve) known bounds for special cases. The lower bounds are generally hitherto unknown. These bounds are characterized as functions of the (i) graph parameters, (ii) eluder dimension of the space of SCMs, denoted by $\operatorname{dim}(\mathcal{F})$, and (iii) the covering number of the function space, denoted by ${\rm cn}(\mathcal{F})$. Specifically, the cumulative achievable regret over horizon $T$ is $\mathcal{O}(K d^{L-1}\sqrt{T\operatorname{dim}(\mathcal{F}) \log({\rm cn}(\mathcal{F}))})$, where $K$ is related to the Lipschitz constants, $d$ is the graph's maximum in-degree, and $L$ is the length of the longest causal path. The upper bound is further refined for special classes of SCMs (neural network, polynomial, and linear), and their corresponding lower bounds are provided.

High-Dimensional Feature Selection for Sample Efficient Treatment Effect Estimation

The estimation of causal treatment effects from observational data is a fundamental problem in causal inference. To avoid bias, the effect estimator must control for all confounders. Hence practitioners often collect data for as many covariates as possible to raise the chances of including the relevant confounders. While this addresses the bias, this has the side effect of significantly increasing the number of data samples required to accurately estimate the effect due to the increased dimensionality. In this work, we consider the setting where out of a large number of covariates $X$ that satisfy strong ignorability, an unknown sparse subset $S$ is sufficient to include to achieve zero bias, i.e. $c$-equivalent to $X$. We propose a common objective function involving outcomes across treatment cohorts with nonconvex joint sparsity regularization that is guaranteed to recover $S$ with high probability under a linear outcome model for $Y$ and subgaussian covariates for each of the treatment cohort. This improves the effect estimation sample complexity so that it scales with the cardinality of the sparse subset $S$ and $\log |X|$, as opposed to the cardinality of the full set $X$. We validate our approach with experiments on treatment effect estimation.