Linear Causal Bandits: Unknown Graph and Soft Interventions

Designing causal bandit algorithms depends on two central categories of assumptions: (i) the extent of information about the underlying causal graphs and (ii) the extent of information about interventional statistical models. There have been extensive recent advances in dispensing with assumptions on either category. These include assuming known graphs but unknown interventional distributions, and the converse setting of assuming unknown graphs but access to restrictive hard/$\operatorname{do}$ interventions, which removes the stochasticity and ancestral dependencies. Nevertheless, the problem in its general form, i.e., unknown graph and unknown stochastic intervention models, remains open. This paper addresses this problem and establishes that in a graph with $N$ nodes, maximum in-degree $d$ and maximum causal path length $L$, after $T$ interaction rounds the regret upper bound scales as $\tilde{\mathcal{O}}((cd)^{L-\frac{1}{2}}\sqrt{T} + d + RN)$ where $c>1$ is a constant and $R$ is a measure of intervention power. A universal minimax lower bound is also established, which scales as $\Omega(d^{L-\frac{3}{2}}\sqrt{T})$. Importantly, the graph size $N$ has a diminishing effect on the regret as $T$ grows. These bounds have matching behavior in $T$, exponential dependence on $L$, and polynomial dependence on $d$ (with the gap $d\ $). On the algorithmic aspect, the paper presents a novel way of designing a computationally efficient CB algorithm, addressing a challenge that the existing CB algorithms using soft interventions face.

Improved Bound for Robust Causal Bandits with Linear Models

This paper investigates the robustness of causal bandits (CBs) in the face of temporal model fluctuations. This setting deviates from the existing literature's widely-adopted assumption of constant causal models. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown and subject to variations over time. The goal is to design a sequence of interventions that incur the smallest cumulative regret compared to an oracle aware of the entire causal model and its fluctuations. A robust CB algorithm is proposed, and its cumulative regret is analyzed by establishing both upper and lower bounds on the regret. It is shown that in a graph with maximum in-degree $d$, length of the largest causal path $L$, and an aggregate model deviation $C$, the regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{T} + C))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T}\; ,\; d^2C\})$. The proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$, maintaining sub-linear regret for a broad range of $C$.

Causal Bandits with General Causal Models and Interventions

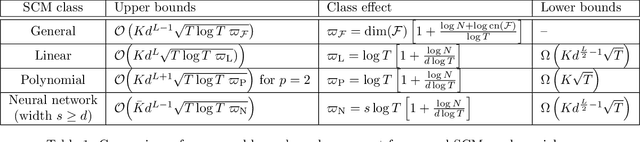
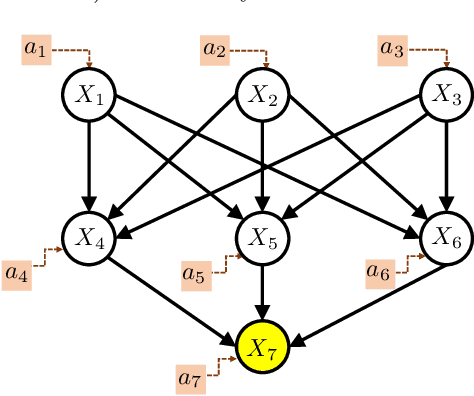
This paper considers causal bandits (CBs) for the sequential design of interventions in a causal system. The objective is to optimize a reward function via minimizing a measure of cumulative regret with respect to the best sequence of interventions in hindsight. The paper advances the results on CBs in three directions. First, the structural causal models (SCMs) are assumed to be unknown and drawn arbitrarily from a general class $\mathcal{F}$ of Lipschitz-continuous functions. Existing results are often focused on (generalized) linear SCMs. Second, the interventions are assumed to be generalized soft with any desired level of granularity, resulting in an infinite number of possible interventions. The existing literature, in contrast, generally adopts atomic and hard interventions. Third, we provide general upper and lower bounds on regret. The upper bounds subsume (and improve) known bounds for special cases. The lower bounds are generally hitherto unknown. These bounds are characterized as functions of the (i) graph parameters, (ii) eluder dimension of the space of SCMs, denoted by $\operatorname{dim}(\mathcal{F})$, and (iii) the covering number of the function space, denoted by ${\rm cn}(\mathcal{F})$. Specifically, the cumulative achievable regret over horizon $T$ is $\mathcal{O}(K d^{L-1}\sqrt{T\operatorname{dim}(\mathcal{F}) \log({\rm cn}(\mathcal{F}))})$, where $K$ is related to the Lipschitz constants, $d$ is the graph's maximum in-degree, and $L$ is the length of the longest causal path. The upper bound is further refined for special classes of SCMs (neural network, polynomial, and linear), and their corresponding lower bounds are provided.

Robust Causal Bandits for Linear Models

Sequential design of experiments for optimizing a reward function in causal systems can be effectively modeled by the sequential design of interventions in causal bandits (CBs). In the existing literature on CBs, a critical assumption is that the causal models remain constant over time. However, this assumption does not necessarily hold in complex systems, which constantly undergo temporal model fluctuations. This paper addresses the robustness of CBs to such model fluctuations. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown. Cumulative regret is adopted as the design criteria, based on which the objective is to design a sequence of interventions that incur the smallest cumulative regret with respect to an oracle aware of the entire causal model and its fluctuations. First, it is established that the existing approaches fail to maintain regret sub-linearity with even a few instances of model deviation. Specifically, when the number of instances with model deviation is as few as $T^\frac{1}{2L}$, where $T$ is the time horizon and $L$ is the longest causal path in the graph, the existing algorithms will have linear regret in $T$. Next, a robust CB algorithm is designed, and its regret is analyzed, where upper and information-theoretic lower bounds on the regret are established. Specifically, in a graph with $N$ nodes and maximum degree $d$, under a general measure of model deviation $C$, the cumulative regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{NT} + NC))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T},d^2C\})$. Comparing these bounds establishes that the proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$ and maintains sub-linear regret for a broader range of $C$.

Image denoising via K-SVD with primal-dual active set algorithm

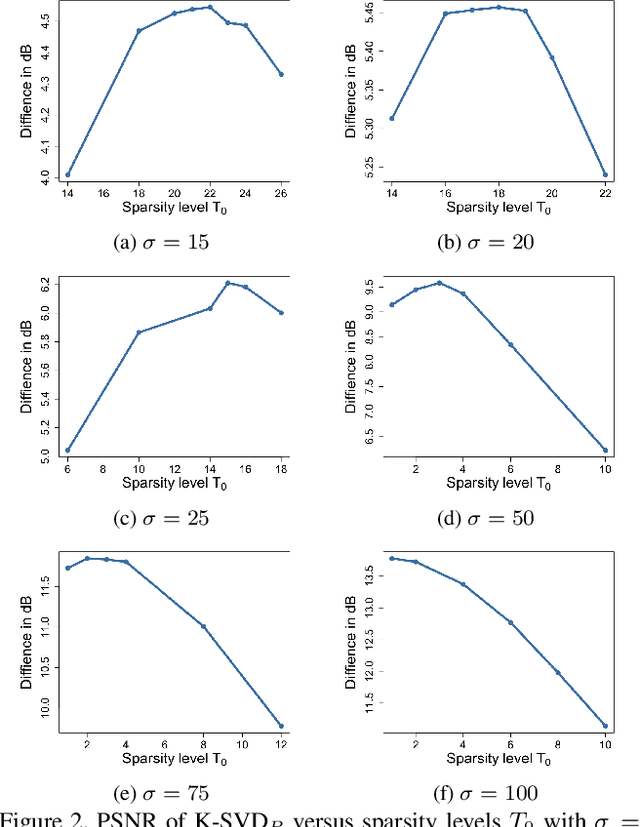
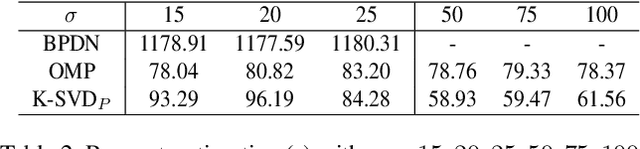
K-SVD algorithm has been successfully applied to image denoising tasks dozens of years but the big bottleneck in speed and accuracy still needs attention to break. For the sparse coding stage in K-SVD, which involves $\ell_{0}$ constraint, prevailing methods usually seek approximate solutions greedily but are less effective once the noise level is high. The alternative $\ell_{1}$ optimization is proved to be powerful than $\ell_{0}$, however, the time consumption prevents it from the implementation. In this paper, we propose a new K-SVD framework called K-SVD$_P$ by applying the Primal-dual active set (PDAS) algorithm to it. Different from the greedy algorithms based K-SVD, the K-SVD$_P$ algorithm develops a selection strategy motivated by KKT (Karush-Kuhn-Tucker) condition and yields to an efficient update in the sparse coding stage. Since the K-SVD$_P$ algorithm seeks for an equivalent solution to the dual problem iteratively with simple explicit expression in this denoising problem, speed and quality of denoising can be reached simultaneously. Experiments are carried out and demonstrate the comparable denoising performance of our K-SVD$_P$ with state-of-the-art methods.