Simultaneous Best Subset Selection and Dimension Reduction via Primal-Dual Iterations

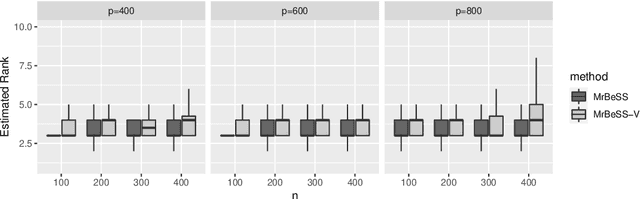
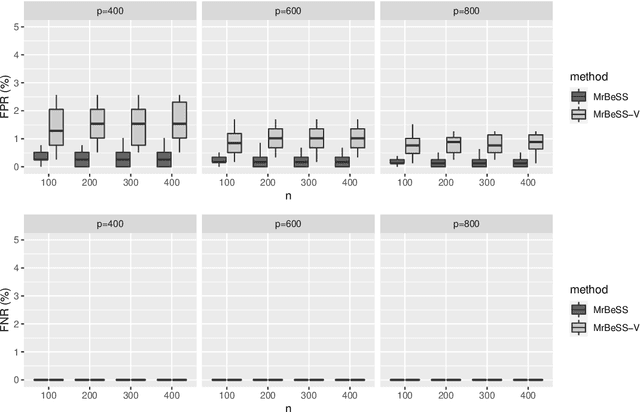
Sparse reduced rank regression is an essential statistical learning method. In the contemporary literature, estimation is typically formulated as a nonconvex optimization that often yields to a local optimum in numerical computation. Yet, their theoretical analysis is always centered on the global optimum, resulting in a discrepancy between the statistical guarantee and the numerical computation. In this research, we offer a new algorithm to address the problem and establish an almost optimal rate for the algorithmic solution. We also demonstrate that the algorithm achieves the estimation with a polynomial number of iterations. In addition, we present a generalized information criterion to simultaneously ensure the consistency of support set recovery and rank estimation. Under the proposed criterion, we show that our algorithm can achieve the oracle reduced rank estimation with a significant probability. The numerical studies and an application in the ovarian cancer genetic data demonstrate the effectiveness and scalability of our approach.

Image denoising via K-SVD with primal-dual active set algorithm

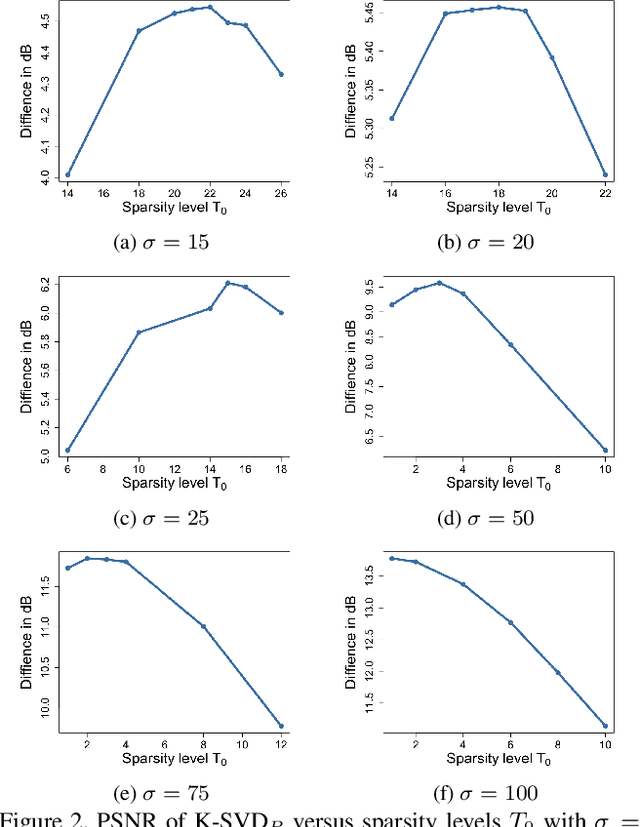
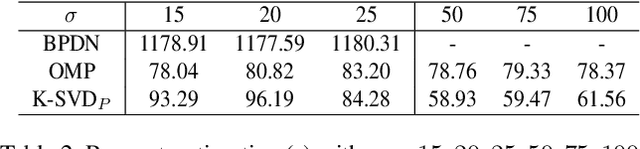
K-SVD algorithm has been successfully applied to image denoising tasks dozens of years but the big bottleneck in speed and accuracy still needs attention to break. For the sparse coding stage in K-SVD, which involves $\ell_{0}$ constraint, prevailing methods usually seek approximate solutions greedily but are less effective once the noise level is high. The alternative $\ell_{1}$ optimization is proved to be powerful than $\ell_{0}$, however, the time consumption prevents it from the implementation. In this paper, we propose a new K-SVD framework called K-SVD$_P$ by applying the Primal-dual active set (PDAS) algorithm to it. Different from the greedy algorithms based K-SVD, the K-SVD$_P$ algorithm develops a selection strategy motivated by KKT (Karush-Kuhn-Tucker) condition and yields to an efficient update in the sparse coding stage. Since the K-SVD$_P$ algorithm seeks for an equivalent solution to the dual problem iteratively with simple explicit expression in this denoising problem, speed and quality of denoising can be reached simultaneously. Experiments are carried out and demonstrate the comparable denoising performance of our K-SVD$_P$ with state-of-the-art methods.