Image denoising via K-SVD with primal-dual active set algorithm
Paper and Code
Jan 19, 2020

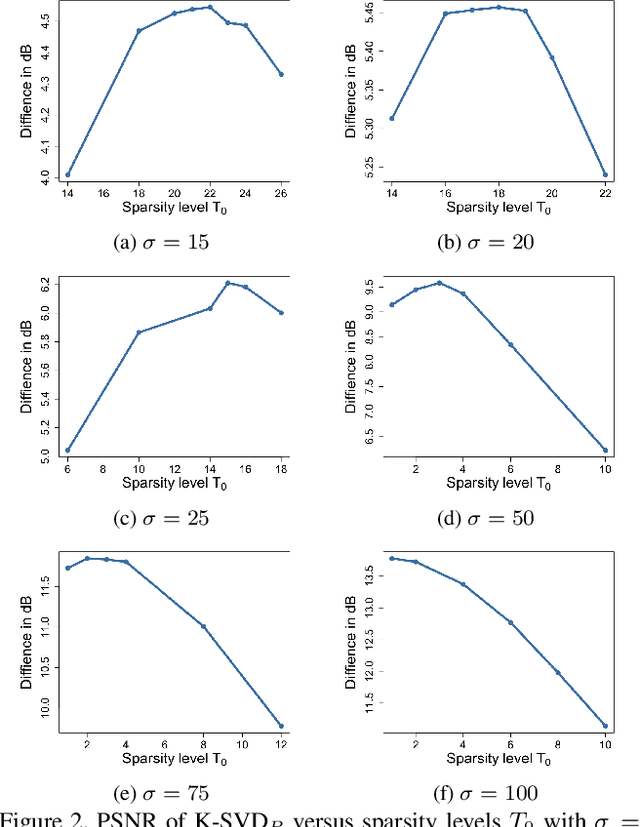
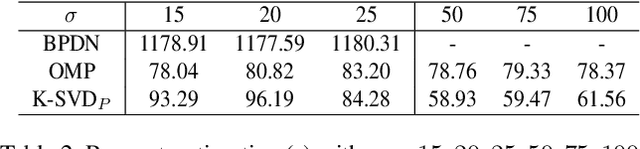
K-SVD algorithm has been successfully applied to image denoising tasks dozens of years but the big bottleneck in speed and accuracy still needs attention to break. For the sparse coding stage in K-SVD, which involves $\ell_{0}$ constraint, prevailing methods usually seek approximate solutions greedily but are less effective once the noise level is high. The alternative $\ell_{1}$ optimization is proved to be powerful than $\ell_{0}$, however, the time consumption prevents it from the implementation. In this paper, we propose a new K-SVD framework called K-SVD$_P$ by applying the Primal-dual active set (PDAS) algorithm to it. Different from the greedy algorithms based K-SVD, the K-SVD$_P$ algorithm develops a selection strategy motivated by KKT (Karush-Kuhn-Tucker) condition and yields to an efficient update in the sparse coding stage. Since the K-SVD$_P$ algorithm seeks for an equivalent solution to the dual problem iteratively with simple explicit expression in this denoising problem, speed and quality of denoising can be reached simultaneously. Experiments are carried out and demonstrate the comparable denoising performance of our K-SVD$_P$ with state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge