A Consistent and Scalable Algorithm for Best Subset Selection in Single Index Models

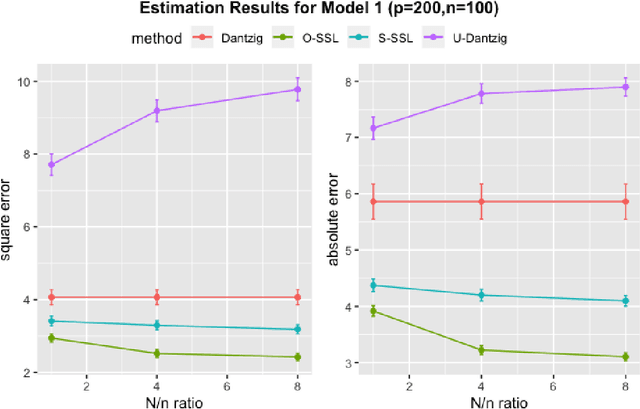
Analysis of high-dimensional data has led to increased interest in both single index models (SIMs) and best subset selection. SIMs provide an interpretable and flexible modeling framework for high-dimensional data, while best subset selection aims to find a sparse model from a large set of predictors. However, best subset selection in high-dimensional models is known to be computationally intractable. Existing methods tend to relax the selection, but do not yield the best subset solution. In this paper, we directly tackle the intractability by proposing the first provably scalable algorithm for best subset selection in high-dimensional SIMs. Our algorithmic solution enjoys the subset selection consistency and has the oracle property with a high probability. The algorithm comprises a generalized information criterion to determine the support size of the regression coefficients, eliminating the model selection tuning. Moreover, our method does not assume an error distribution or a specific link function and hence is flexible to apply. Extensive simulation results demonstrate that our method is not only computationally efficient but also able to exactly recover the best subset in various settings (e.g., linear regression, Poisson regression, heteroscedastic models).

Simultaneous Best Subset Selection and Dimension Reduction via Primal-Dual Iterations

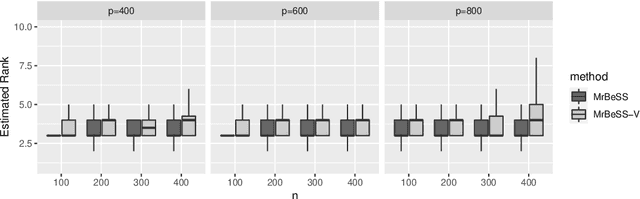
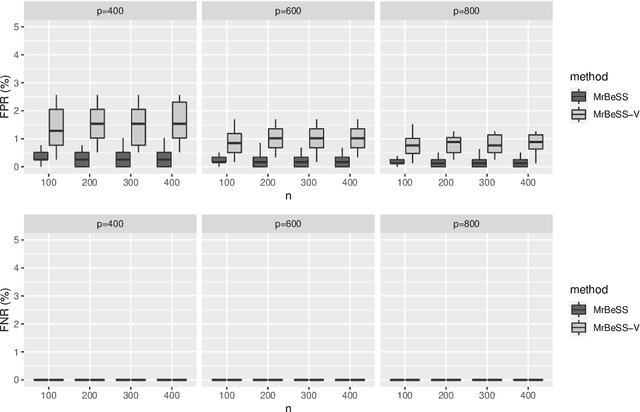
Sparse reduced rank regression is an essential statistical learning method. In the contemporary literature, estimation is typically formulated as a nonconvex optimization that often yields to a local optimum in numerical computation. Yet, their theoretical analysis is always centered on the global optimum, resulting in a discrepancy between the statistical guarantee and the numerical computation. In this research, we offer a new algorithm to address the problem and establish an almost optimal rate for the algorithmic solution. We also demonstrate that the algorithm achieves the estimation with a polynomial number of iterations. In addition, we present a generalized information criterion to simultaneously ensure the consistency of support set recovery and rank estimation. Under the proposed criterion, we show that our algorithm can achieve the oracle reduced rank estimation with a significant probability. The numerical studies and an application in the ovarian cancer genetic data demonstrate the effectiveness and scalability of our approach.

Optimal Semi-supervised Estimation and Inference for High-dimensional Linear Regression

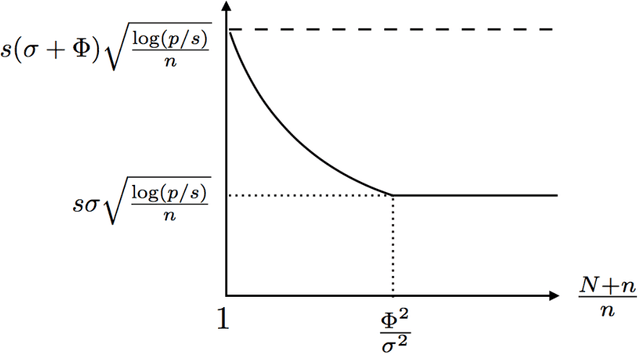
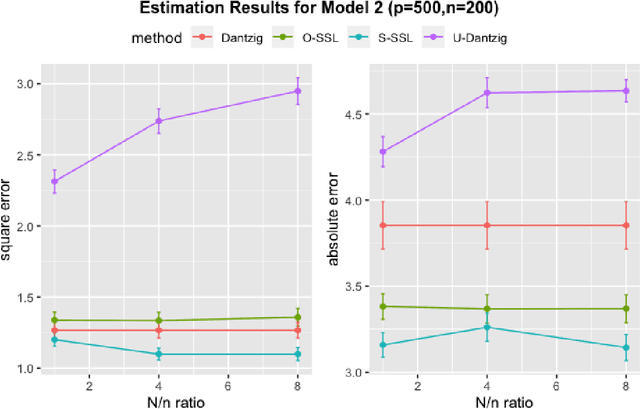
There are many scenarios such as the electronic health records where the outcome is much more difficult to collect than the covariates. In this paper, we consider the linear regression problem with such a data structure under the high dimensionality. Our goal is to investigate when and how the unlabeled data can be exploited to improve the estimation and inference of the regression parameters in linear models, especially in light of the fact that such linear models may be misspecified in data analysis. In particular, we address the following two important questions. (1) Can we use the labeled data as well as the unlabeled data to construct a semi-supervised estimator such that its convergence rate is faster than the supervised estimators? (2) Can we construct confidence intervals or hypothesis tests that are guaranteed to be more efficient or powerful than the supervised estimators? To address the first question, we establish the minimax lower bound for parameter estimation in the semi-supervised setting. We show that the upper bound from the supervised estimators that only use the labeled data cannot attain this lower bound. We close this gap by proposing a new semi-supervised estimator which attains the lower bound. To address the second question, based on our proposed semi-supervised estimator, we propose two additional estimators for semi-supervised inference, the efficient estimator and the safe estimator. The former is fully efficient if the unknown conditional mean function is estimated consistently, but may not be more efficient than the supervised approach otherwise. The latter usually does not aim to provide fully efficient inference, but is guaranteed to be no worse than the supervised approach, no matter whether the linear model is correctly specified or the conditional mean function is consistently estimated.