Coverage Analysis of Downlink Transmission in Multi-Connectivity Cellular V2X Networks

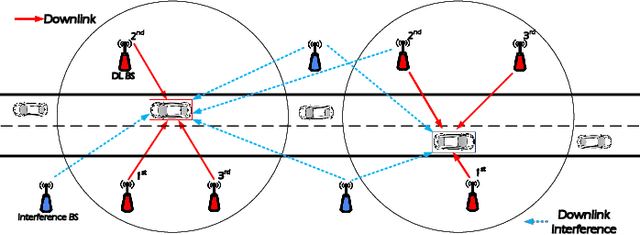
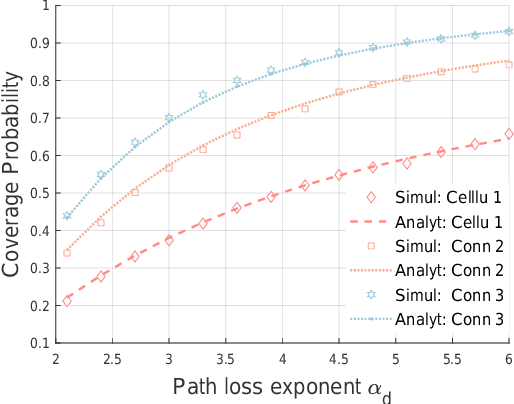
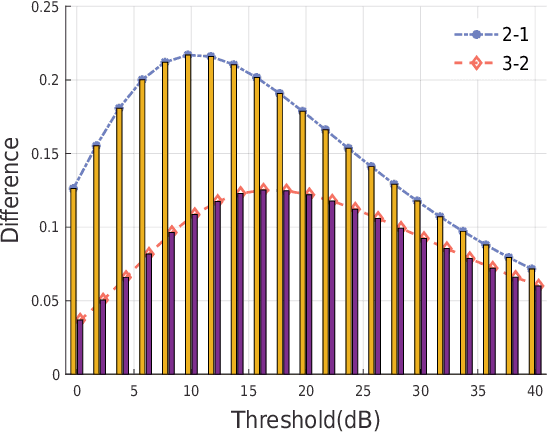
With the increasing of connected vehicles in the fifth-generation mobile communication networks (5G) and beyond 5G (B5G), ensuring the reliable and high-speed cellular vehicle-to-everything (C-V2X) communication has posed significant challenges due to the high mobility of vehicles. For improving the network performance and reliability, multi-connectivity technology has emerged as a crucial transmission mode for C-V2X in the 5G era. To this end, this paper proposes a framework for analyzing the performance of multi-connectivity in C-V2X downlink transmission, with a focus on the performance indicators of joint distance distribution and coverage probability. Specifically, we first derive the joint distance distribution of multi-connectivity. By leveraging the tools of stochastic geometry, we then obtain the analytical expressions of coverage probability based on the previous results for general multi-connectivity cases in C-V2X. Subsequently, we evaluate the effect of path loss exponent and downlink base station density on coverage probability based on the proposed analytical framework. Finally, extensive Monte Carlo simulations are conducted to validate the effectiveness of the proposed analytical framework and the simulation results reveal that multi-connectivity technology can significantly enhance the coverage probability in C-V2X.

Performance Analysis for Downlink Transmission in Multi-Connectivity Cellular V2X Networks

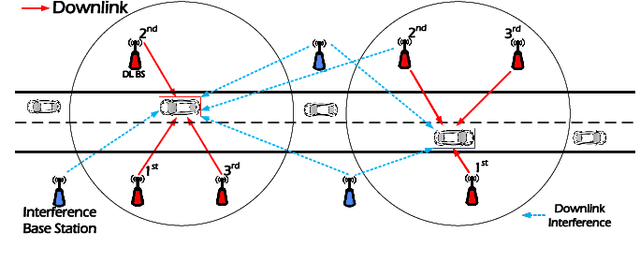
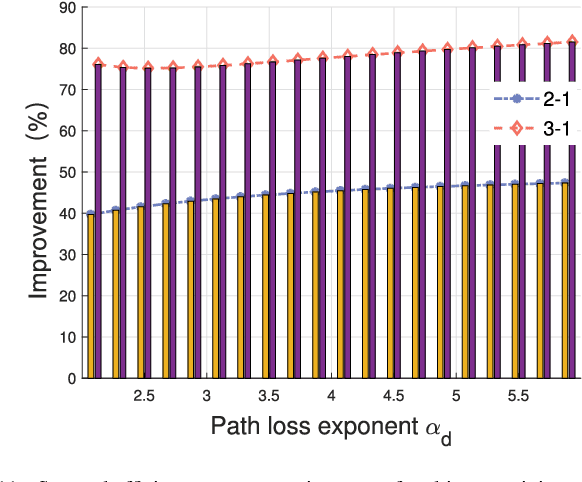
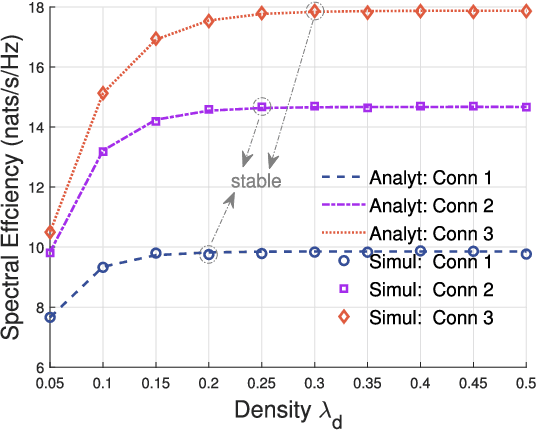
With the ever-increasing number of connected vehicles in the fifth-generation mobile communication networks (5G) and beyond 5G (B5G), ensuring the reliability and high-speed demand of cellular vehicle-to-everything (C-V2X) communication in scenarios where vehicles are moving at high speeds poses a significant challenge.Recently, multi-connectivity technology has become a promising network access paradigm for improving network performance and reliability for C-V2X in the 5G and B5G era. To this end, this paper proposes an analytical framework for the performance of downlink in multi-connectivity C-V2X networks. Specifically, by modeling the vehicles and base stations as one-dimensional Poisson point processes, we first derive and analyze the joint distance distribution of multi-connectivity. Then through leveraging the tools of stochastic geometry, the coverage probability and spectral efficiency are obtained based on the previous results for general multi-connectivity cases in C-V2X. Additionally, we evaluate the effect of path loss exponent and the density of downlink base station on system performance indicators. We demonstrate through extensive Monte Carlo simulations that multi-connectivity technology can effectively enhance network performance in C-V2X. Our findings have important implications for the research and application of multi-connectivity C-V2X in the 5G and B5G era.

ReTaSA: A Nonparametric Functional Estimation Approach for Addressing Continuous Target Shift

The presence of distribution shifts poses a significant challenge for deploying modern machine learning models in real-world applications. This work focuses on the target shift problem in a regression setting (Zhang et al., 2013; Nguyen et al., 2016). More specifically, the target variable y (also known as the response variable), which is continuous, has different marginal distributions in the training source and testing domain, while the conditional distribution of features x given y remains the same. While most literature focuses on classification tasks with finite target space, the regression problem has an infinite dimensional target space, which makes many of the existing methods inapplicable. In this work, we show that the continuous target shift problem can be addressed by estimating the importance weight function from an ill-posed integral equation. We propose a nonparametric regularized approach named ReTaSA to solve the ill-posed integral equation and provide theoretical justification for the estimated importance weight function. The effectiveness of the proposed method has been demonstrated with extensive numerical studies on synthetic and real-world datasets.

Channel-Feedback-Free Transmission for Downlink FD-RAN: A Radio Map based Complex-valued Precoding Network Approach

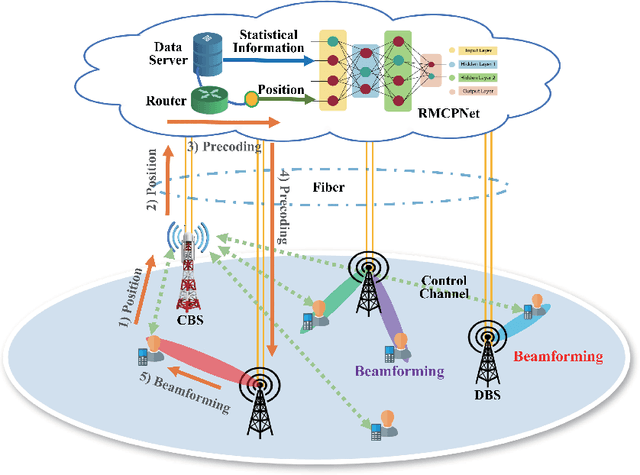
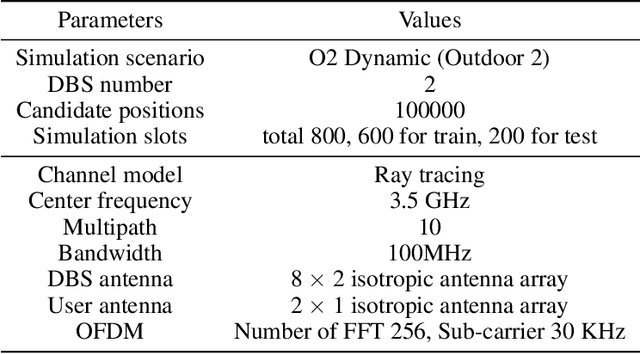
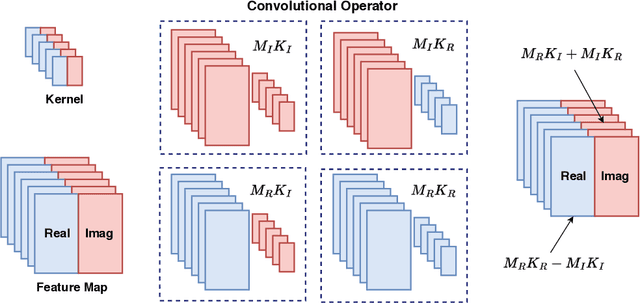
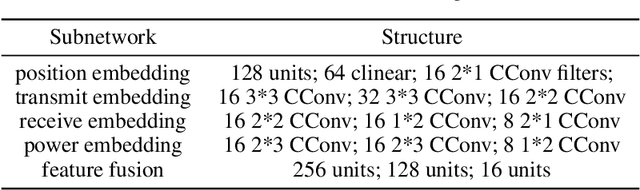
As the demand for high-quality services proliferates, an innovative network architecture, the fully-decoupled RAN (FD-RAN), has emerged for more flexible spectrum resource utilization and lower network costs. However, with the decoupling of uplink base stations and downlink base stations in FD-RAN, the traditional transmission mechanism, which relies on real-time channel feedback, is not suitable as the receiver is not able to feedback accurate and timely channel state information to the transmitter. This paper proposes a novel transmission scheme without relying on physical layer channel feedback. Specifically, we design a radio map based complex-valued precoding network~(RMCPNet) model, which outputs the base station precoding based on user location. RMCPNet comprises multiple subnets, with each subnet responsible for extracting unique modal features from diverse input modalities. Furthermore, the multi-modal embeddings derived from these distinct subnets are integrated within the information fusion layer, culminating in a unified representation. We also develop a specific RMCPNet training algorithm that employs the negative spectral efficiency as the loss function. We evaluate the performance of the proposed scheme on the public DeepMIMO dataset and show that RMCPNet can achieve 16\% and 76\% performance improvements over the conventional real-valued neural network and statistical codebook approach, respectively.

Assumption-lean and Data-adaptive Post-Prediction Inference

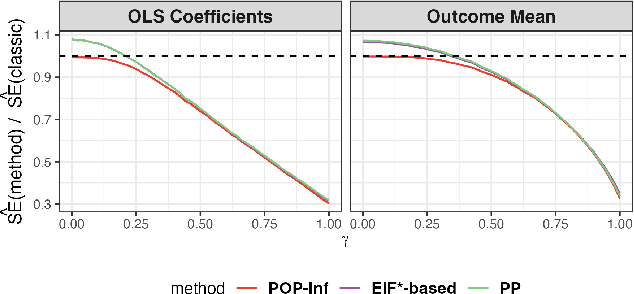
A primary challenge facing modern scientific research is the limited availability of gold-standard data which can be both costly and labor-intensive to obtain. With the rapid development of machine learning (ML), scientists have relied on ML algorithms to predict these gold-standard outcomes with easily obtained covariates. However, these predicted outcomes are often used directly in subsequent statistical analyses, ignoring imprecision and heterogeneity introduced by the prediction procedure. This will likely result in false positive findings and invalid scientific conclusions. In this work, we introduce an assumption-lean and data-adaptive Post-Prediction Inference (POP-Inf) procedure that allows valid and powerful inference based on ML-predicted outcomes. Its "assumption-lean" property guarantees reliable statistical inference without assumptions on the ML-prediction, for a wide range of statistical quantities. Its "data-adaptive'" feature guarantees an efficiency gain over existing post-prediction inference methods, regardless of the accuracy of ML-prediction. We demonstrate the superiority and applicability of our method through simulations and large-scale genomic data.

Sufficient Identification Conditions and Semiparametric Estimation under Missing Not at Random Mechanisms

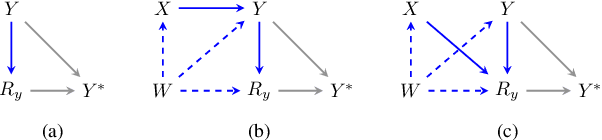
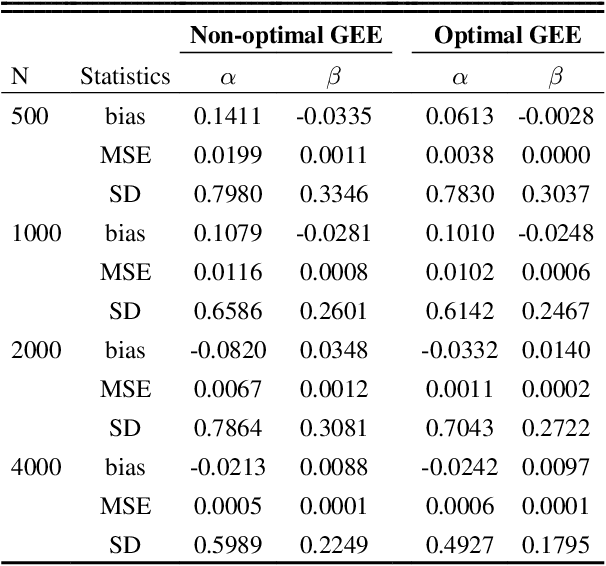
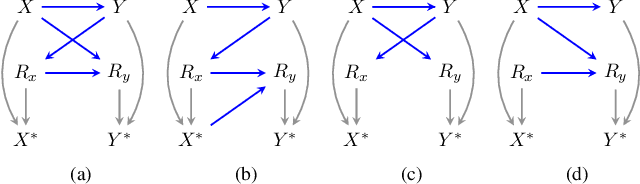
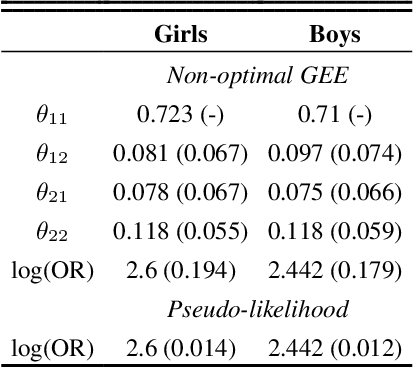
Conducting valid statistical analyses is challenging in the presence of missing-not-at-random (MNAR) data, where the missingness mechanism is dependent on the missing values themselves even conditioned on the observed data. Here, we consider a MNAR model that generalizes several prior popular MNAR models in two ways: first, it is less restrictive in terms of statistical independence assumptions imposed on the underlying joint data distribution, and second, it allows for all variables in the observed sample to have missing values. This MNAR model corresponds to a so-called criss-cross structure considered in the literature on graphical models of missing data that prevents nonparametric identification of the entire missing data model. Nonetheless, part of the complete-data distribution remains nonparametrically identifiable. By exploiting this fact and considering a rich class of exponential family distributions, we establish sufficient conditions for identification of the complete-data distribution as well as the entire missingness mechanism. We then propose methods for testing the independence restrictions encoded in such models using odds ratio as our parameter of interest. We adopt two semiparametric approaches for estimating the odds ratio parameter and establish the corresponding asymptotic theories: one involves maximizing a conditional likelihood with order statistics and the other uses estimating equations. The utility of our methods is illustrated via simulation studies.

ELSA: Efficient Label Shift Adaptation through the Lens of Semiparametric Models

We study the domain adaptation problem with label shift in this work. Under the label shift context, the marginal distribution of the label varies across the training and testing datasets, while the conditional distribution of features given the label is the same. Traditional label shift adaptation methods either suffer from large estimation errors or require cumbersome post-prediction calibrations. To address these issues, we first propose a moment-matching framework for adapting the label shift based on the geometry of the influence function. Under such a framework, we propose a novel method named \underline{E}fficient \underline{L}abel \underline{S}hift \underline{A}daptation (ELSA), in which the adaptation weights can be estimated by solving linear systems. Theoretically, the ELSA estimator is $\sqrt{n}$-consistent ($n$ is the sample size of the source data) and asymptotically normal. Empirically, we show that ELSA can achieve state-of-the-art estimation performances without post-prediction calibrations, thus, gaining computational efficiency.

Optimal Semi-supervised Estimation and Inference for High-dimensional Linear Regression

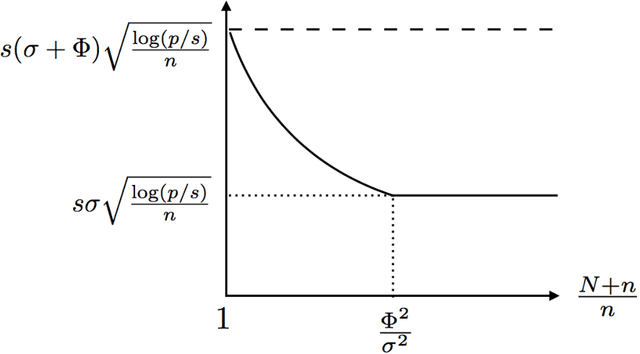
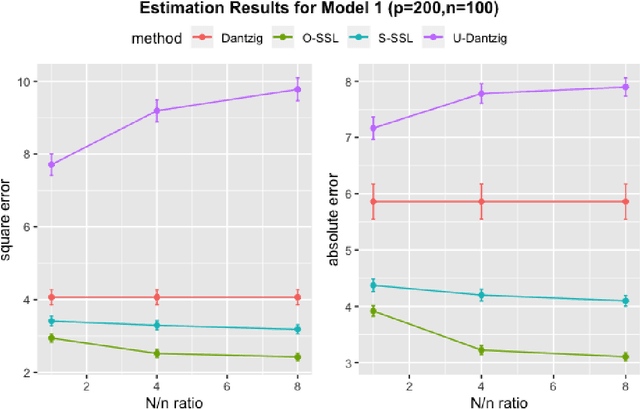
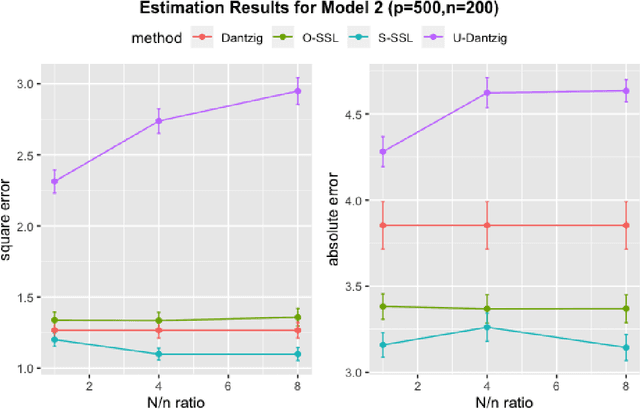
There are many scenarios such as the electronic health records where the outcome is much more difficult to collect than the covariates. In this paper, we consider the linear regression problem with such a data structure under the high dimensionality. Our goal is to investigate when and how the unlabeled data can be exploited to improve the estimation and inference of the regression parameters in linear models, especially in light of the fact that such linear models may be misspecified in data analysis. In particular, we address the following two important questions. (1) Can we use the labeled data as well as the unlabeled data to construct a semi-supervised estimator such that its convergence rate is faster than the supervised estimators? (2) Can we construct confidence intervals or hypothesis tests that are guaranteed to be more efficient or powerful than the supervised estimators? To address the first question, we establish the minimax lower bound for parameter estimation in the semi-supervised setting. We show that the upper bound from the supervised estimators that only use the labeled data cannot attain this lower bound. We close this gap by proposing a new semi-supervised estimator which attains the lower bound. To address the second question, based on our proposed semi-supervised estimator, we propose two additional estimators for semi-supervised inference, the efficient estimator and the safe estimator. The former is fully efficient if the unknown conditional mean function is estimated consistently, but may not be more efficient than the supervised approach otherwise. The latter usually does not aim to provide fully efficient inference, but is guaranteed to be no worse than the supervised approach, no matter whether the linear model is correctly specified or the conditional mean function is consistently estimated.

Nonregular and Minimax Estimation of Individualized Thresholds in High Dimension with Binary Responses

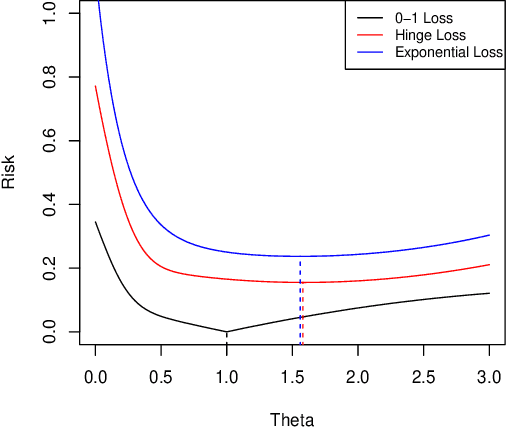
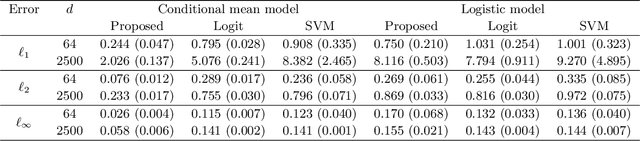
Given a large number of covariates $Z$, we consider the estimation of a high-dimensional parameter $\theta$ in an individualized linear threshold $\theta^T Z$ for a continuous variable $X$, which minimizes the disagreement between $\text{sign}(X-\theta^TZ)$ and a binary response $Y$. While the problem can be formulated into the M-estimation framework, minimizing the corresponding empirical risk function is computationally intractable due to discontinuity of the sign function. Moreover, estimating $\theta$ even in the fixed-dimensional setting is known as a nonregular problem leading to nonstandard asymptotic theory. To tackle the computational and theoretical challenges in the estimation of the high-dimensional parameter $\theta$, we propose an empirical risk minimization approach based on a regularized smoothed loss function. The statistical and computational trade-off of the algorithm is investigated. Statistically, we show that the finite sample error bound for estimating $\theta$ in $\ell_2$ norm is $(s\log d/n)^{\beta/(2\beta+1)}$, where $d$ is the dimension of $\theta$, $s$ is the sparsity level, $n$ is the sample size and $\beta$ is the smoothness of the conditional density of $X$ given the response $Y$ and the covariates $Z$. The convergence rate is nonstandard and slower than that in the classical Lasso problems. Furthermore, we prove that the resulting estimator is minimax rate optimal up to a logarithmic factor. The Lepski's method is developed to achieve the adaption to the unknown sparsity $s$ and smoothness $\beta$. Computationally, an efficient path-following algorithm is proposed to compute the solution path. We show that this algorithm achieves geometric rate of convergence for computing the whole path. Finally, we evaluate the finite sample performance of the proposed estimator in simulation studies and a real data analysis.