MissNODAG: Differentiable Cyclic Causal Graph Learning from Incomplete Data

Causal discovery in real-world systems, such as biological networks, is often complicated by feedback loops and incomplete data. Standard algorithms, which assume acyclic structures or fully observed data, struggle with these challenges. To address this gap, we propose MissNODAG, a differentiable framework for learning both the underlying cyclic causal graph and the missingness mechanism from partially observed data, including data missing not at random. Our framework integrates an additive noise model with an expectation-maximization procedure, alternating between imputing missing values and optimizing the observed data likelihood, to uncover both the cyclic structures and the missingness mechanism. We demonstrate the effectiveness of MissNODAG through synthetic experiments and an application to real-world gene perturbation data.

Average Causal Effect Estimation in DAGs with Hidden Variables: Extensions of Back-Door and Front-Door Criteria

The identification theory for causal effects in directed acyclic graphs (DAGs) with hidden variables is well-developed, but methods for estimating and inferring functionals beyond the g-formula remain limited. Previous studies have proposed semiparametric estimators for identifiable functionals in a broad class of DAGs with hidden variables. While demonstrating double robustness in some models, existing estimators face challenges, particularly with density estimation and numerical integration for continuous variables, and their estimates may fall outside the parameter space of the target estimand. Their asymptotic properties are also underexplored, especially when using flexible statistical and machine learning models for nuisance estimation. This study addresses these challenges by introducing novel one-step corrected plug-in and targeted minimum loss-based estimators of causal effects for a class of DAGs that extend classical back-door and front-door criteria (known as the treatment primal fixability criterion in prior literature). These estimators leverage machine learning to minimize modeling assumptions while ensuring key statistical properties such as asymptotic linearity, double robustness, efficiency, and staying within the bounds of the target parameter space. We establish conditions for nuisance functional estimates in terms of L2(P)-norms to achieve root-n consistent causal effect estimates. To facilitate practical application, we have developed the flexCausal package in R.

Fair Risk Minimization under Causal Path-Specific Effect Constraints

This paper introduces a framework for estimating fair optimal predictions using machine learning where the notion of fairness can be quantified using path-specific causal effects. We use a recently developed approach based on Lagrange multipliers for infinite-dimensional functional estimation to derive closed-form solutions for constrained optimization based on mean squared error and cross-entropy risk criteria. The theoretical forms of the solutions are analyzed in detail and described as nuanced adjustments to the unconstrained minimizer. This analysis highlights important trade-offs between risk minimization and achieving fairnes. The theoretical solutions are also used as the basis for construction of flexible semiparametric estimation strategies for these nuisance components. We describe the robustness properties of our estimators in terms of achieving the optimal constrained risk, as well as in terms of controlling the value of the constraint. We study via simulation the impact of using robust estimators of pathway-specific effects to validate our theory. This work advances the discourse on algorithmic fairness by integrating complex causal considerations into model training, thus providing strategies for implementing fair models in real-world applications.

Statistical learning for constrained functional parameters in infinite-dimensional models with applications in fair machine learning

Constrained learning has become increasingly important, especially in the realm of algorithmic fairness and machine learning. In these settings, predictive models are developed specifically to satisfy pre-defined notions of fairness. Here, we study the general problem of constrained statistical machine learning through a statistical functional lens. We consider learning a function-valued parameter of interest under the constraint that one or several pre-specified real-valued functional parameters equal zero or are otherwise bounded. We characterize the constrained functional parameter as the minimizer of a penalized risk criterion using a Lagrange multiplier formulation. We show that closed-form solutions for the optimal constrained parameter are often available, providing insight into mechanisms that drive fairness in predictive models. Our results also suggest natural estimators of the constrained parameter that can be constructed by combining estimates of unconstrained parameters of the data generating distribution. Thus, our estimation procedure for constructing fair machine learning algorithms can be applied in conjunction with any statistical learning approach and off-the-shelf software. We demonstrate the generality of our method by explicitly considering a number of examples of statistical fairness constraints and implementing the approach using several popular learning approaches.

Targeted Machine Learning for Average Causal Effect Estimation Using the Front-Door Functional

Evaluating the average causal effect (ACE) of a treatment on an outcome often involves overcoming the challenges posed by confounding factors in observational studies. A traditional approach uses the back-door criterion, seeking adjustment sets to block confounding paths between treatment and outcome. However, this method struggles with unmeasured confounders. As an alternative, the front-door criterion offers a solution, even in the presence of unmeasured confounders between treatment and outcome. This method relies on identifying mediators that are not directly affected by these confounders and that completely mediate the treatment's effect. Here, we introduce novel estimation strategies for the front-door criterion based on the targeted minimum loss-based estimation theory. Our estimators work across diverse scenarios, handling binary, continuous, and multivariate mediators. They leverage data-adaptive machine learning algorithms, minimizing assumptions and ensuring key statistical properties like asymptotic linearity, double-robustness, efficiency, and valid estimates within the target parameter space. We establish conditions under which the nuisance functional estimations ensure the root n-consistency of ACE estimators. Our numerical experiments show the favorable finite sample performance of the proposed estimators. We demonstrate the applicability of these estimators to analyze the effect of early stage academic performance on future yearly income using data from the Finnish Social Science Data Archive.

Sufficient Identification Conditions and Semiparametric Estimation under Missing Not at Random Mechanisms

Conducting valid statistical analyses is challenging in the presence of missing-not-at-random (MNAR) data, where the missingness mechanism is dependent on the missing values themselves even conditioned on the observed data. Here, we consider a MNAR model that generalizes several prior popular MNAR models in two ways: first, it is less restrictive in terms of statistical independence assumptions imposed on the underlying joint data distribution, and second, it allows for all variables in the observed sample to have missing values. This MNAR model corresponds to a so-called criss-cross structure considered in the literature on graphical models of missing data that prevents nonparametric identification of the entire missing data model. Nonetheless, part of the complete-data distribution remains nonparametrically identifiable. By exploiting this fact and considering a rich class of exponential family distributions, we establish sufficient conditions for identification of the complete-data distribution as well as the entire missingness mechanism. We then propose methods for testing the independence restrictions encoded in such models using odds ratio as our parameter of interest. We adopt two semiparametric approaches for estimating the odds ratio parameter and establish the corresponding asymptotic theories: one involves maximizing a conditional likelihood with order statistics and the other uses estimating equations. The utility of our methods is illustrated via simulation studies.

Learning Task-Aware Effective Brain Connectivity for fMRI Analysis with Graph Neural Networks

Functional magnetic resonance imaging (fMRI) has become one of the most common imaging modalities for brain function analysis. Recently, graph neural networks (GNN) have been adopted for fMRI analysis with superior performance. Unfortunately, traditional functional brain networks are mainly constructed based on similarities among region of interests (ROI), which are noisy and agnostic to the downstream prediction tasks and can lead to inferior results for GNN-based models. To better adapt GNNs for fMRI analysis, we propose TBDS, an end-to-end framework based on \underline{T}ask-aware \underline{B}rain connectivity \underline{D}AG (short for Directed Acyclic Graph) \underline{S}tructure generation for fMRI analysis. The key component of TBDS is the brain network generator which adopts a DAG learning approach to transform the raw time-series into task-aware brain connectivities. Besides, we design an additional contrastive regularization to inject task-specific knowledge during the brain network generation process. Comprehensive experiments on two fMRI datasets, namely Adolescent Brain Cognitive Development (ABCD) and Philadelphia Neuroimaging Cohort (PNC) datasets demonstrate the efficacy of TBDS. In addition, the generated brain networks also highlight the prediction-related brain regions and thus provide unique interpretations of the prediction results. Our implementation will be published to https://github.com/yueyu1030/TBDS upon acceptance.

Causal and counterfactual views of missing data models

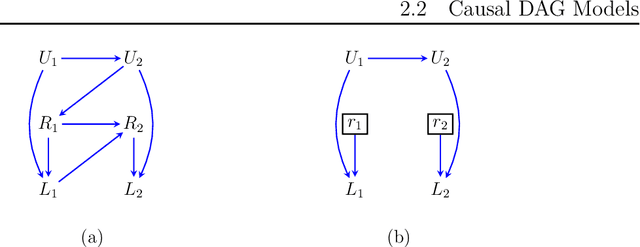
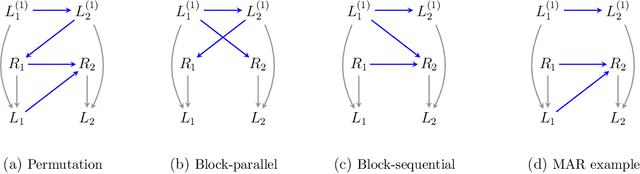
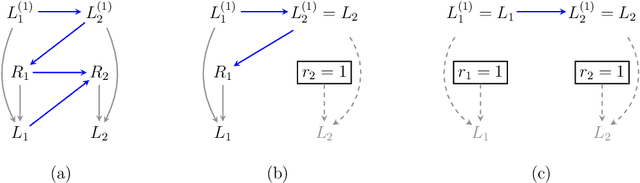
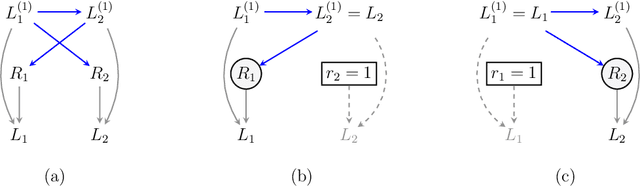
It is often said that the fundamental problem of causal inference is a missing data problem -- the comparison of responses to two hypothetical treatment assignments is made difficult because for every experimental unit only one potential response is observed. In this paper, we consider the implications of the converse view: that missing data problems are a form of causal inference. We make explicit how the missing data problem of recovering the complete data law from the observed law can be viewed as identification of a joint distribution over counterfactual variables corresponding to values had we (possibly contrary to fact) been able to observe them. Drawing analogies with causal inference, we show how identification assumptions in missing data can be encoded in terms of graphical models defined over counterfactual and observed variables. We review recent results in missing data identification from this viewpoint. In doing so, we note interesting similarities and differences between missing data and causal identification theories.

On Testability of the Front-Door Model via Verma Constraints

The front-door criterion can be used to identify and compute causal effects despite the existence of unmeasured confounders between a treatment and outcome. However, the key assumptions -- (i) the existence of a variable (or set of variables) that fully mediates the effect of the treatment on the outcome, and (ii) which simultaneously does not suffer from similar issues of confounding as the treatment-outcome pair -- are often deemed implausible. This paper explores the testability of these assumptions. We show that under mild conditions involving an auxiliary variable, the assumptions encoded in the front-door model (and simple extensions of it) may be tested via generalized equality constraints a.k.a Verma constraints. We propose two goodness-of-fit tests based on this observation, and evaluate the efficacy of our proposal on real and synthetic data. We also provide theoretical and empirical comparisons to instrumental variable approaches to handling unmeasured confounding.

On Testability and Goodness of Fit Tests in Missing Data Models

Significant progress has been made in developing identification and estimation techniques for missing data problems where modeling assumptions can be described via a directed acyclic graph. The validity of results using such techniques rely on the assumptions encoded by the graph holding true; however, verification of these assumptions has not received sufficient attention in prior work. In this paper, we provide new insights on the testable implications of three broad classes of missing data graphical models, and design goodness-of-fit tests around them. The classes of models explored are: sequential missing-at-random and missing-not-at-random models which can be used for modeling longitudinal studies with dropout/censoring, and a kind of no self-censoring model which can be applied to cross-sectional studies and surveys.