David Benkeser
Assessing Racial Disparities in Healthcare Expenditures Using Causal Path-Specific Effects
Apr 30, 2025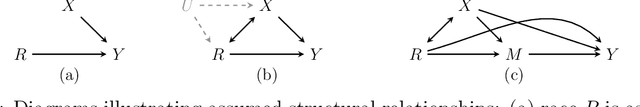


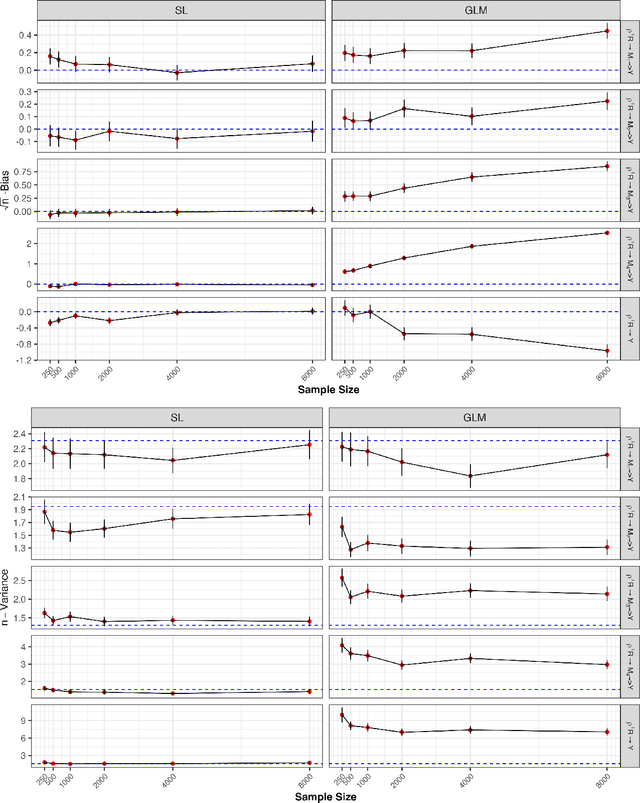
Abstract:Racial disparities in healthcare expenditures are well-documented, yet the underlying drivers remain complex and require further investigation. This study employs causal and counterfactual path-specific effects to quantify how various factors, including socioeconomic status, insurance access, health behaviors, and health status, mediate these disparities. Using data from the Medical Expenditures Panel Survey, we estimate how expenditures would differ under counterfactual scenarios in which the values of specific mediators were aligned across racial groups along selected causal pathways. A key challenge in this analysis is ensuring robustness against model misspecification while addressing the zero-inflation and right-skewness of healthcare expenditures. For reliable inference, we derive asymptotically linear estimators by integrating influence function-based techniques with flexible machine learning methods, including super learners and a two-part model tailored to the zero-inflated, right-skewed nature of healthcare expenditures.
A Density Ratio Super Learner
Aug 09, 2024Abstract:The estimation of the ratio of two density probability functions is of great interest in many statistics fields, including causal inference. In this study, we develop an ensemble estimator of density ratios with a novel loss function based on super learning. We show that this novel loss function is qualified for building super learners. Two simulations corresponding to mediation analysis and longitudinal modified treatment policy in causal inference, where density ratios are nuisance parameters, are conducted to show our density ratio super learner's performance empirically.
Fair Risk Minimization under Causal Path-Specific Effect Constraints
Aug 03, 2024



Abstract:This paper introduces a framework for estimating fair optimal predictions using machine learning where the notion of fairness can be quantified using path-specific causal effects. We use a recently developed approach based on Lagrange multipliers for infinite-dimensional functional estimation to derive closed-form solutions for constrained optimization based on mean squared error and cross-entropy risk criteria. The theoretical forms of the solutions are analyzed in detail and described as nuanced adjustments to the unconstrained minimizer. This analysis highlights important trade-offs between risk minimization and achieving fairnes. The theoretical solutions are also used as the basis for construction of flexible semiparametric estimation strategies for these nuisance components. We describe the robustness properties of our estimators in terms of achieving the optimal constrained risk, as well as in terms of controlling the value of the constraint. We study via simulation the impact of using robust estimators of pathway-specific effects to validate our theory. This work advances the discourse on algorithmic fairness by integrating complex causal considerations into model training, thus providing strategies for implementing fair models in real-world applications.
Statistical learning for constrained functional parameters in infinite-dimensional models with applications in fair machine learning
Apr 15, 2024

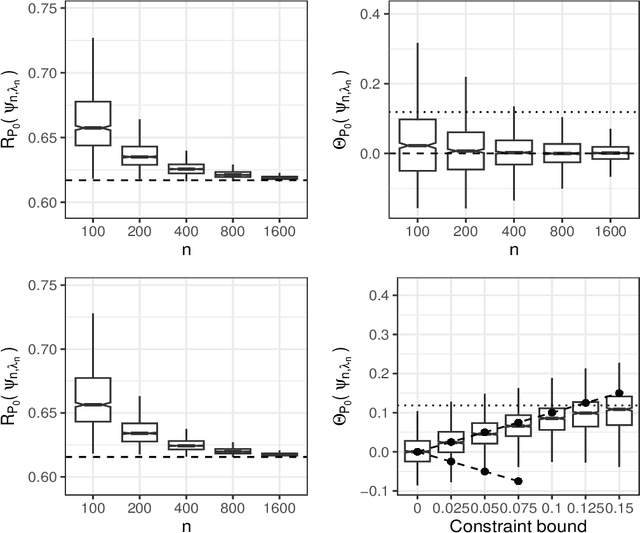
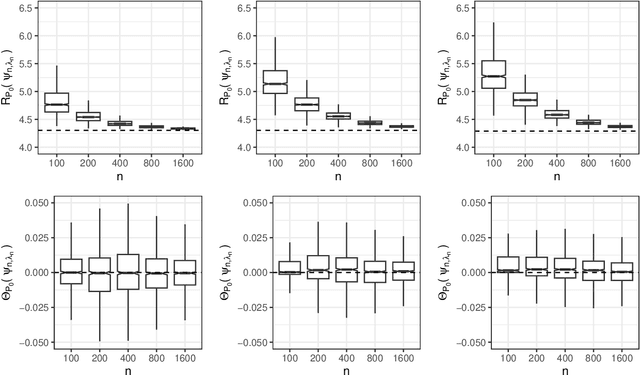
Abstract:Constrained learning has become increasingly important, especially in the realm of algorithmic fairness and machine learning. In these settings, predictive models are developed specifically to satisfy pre-defined notions of fairness. Here, we study the general problem of constrained statistical machine learning through a statistical functional lens. We consider learning a function-valued parameter of interest under the constraint that one or several pre-specified real-valued functional parameters equal zero or are otherwise bounded. We characterize the constrained functional parameter as the minimizer of a penalized risk criterion using a Lagrange multiplier formulation. We show that closed-form solutions for the optimal constrained parameter are often available, providing insight into mechanisms that drive fairness in predictive models. Our results also suggest natural estimators of the constrained parameter that can be constructed by combining estimates of unconstrained parameters of the data generating distribution. Thus, our estimation procedure for constructing fair machine learning algorithms can be applied in conjunction with any statistical learning approach and off-the-shelf software. We demonstrate the generality of our method by explicitly considering a number of examples of statistical fairness constraints and implementing the approach using several popular learning approaches.
Targeted Machine Learning for Average Causal Effect Estimation Using the Front-Door Functional
Dec 15, 2023Abstract:Evaluating the average causal effect (ACE) of a treatment on an outcome often involves overcoming the challenges posed by confounding factors in observational studies. A traditional approach uses the back-door criterion, seeking adjustment sets to block confounding paths between treatment and outcome. However, this method struggles with unmeasured confounders. As an alternative, the front-door criterion offers a solution, even in the presence of unmeasured confounders between treatment and outcome. This method relies on identifying mediators that are not directly affected by these confounders and that completely mediate the treatment's effect. Here, we introduce novel estimation strategies for the front-door criterion based on the targeted minimum loss-based estimation theory. Our estimators work across diverse scenarios, handling binary, continuous, and multivariate mediators. They leverage data-adaptive machine learning algorithms, minimizing assumptions and ensuring key statistical properties like asymptotic linearity, double-robustness, efficiency, and valid estimates within the target parameter space. We establish conditions under which the nuisance functional estimations ensure the root n-consistency of ACE estimators. Our numerical experiments show the favorable finite sample performance of the proposed estimators. We demonstrate the applicability of these estimators to analyze the effect of early stage academic performance on future yearly income using data from the Finnish Social Science Data Archive.
A Huber loss-based super learner with applications to healthcare expenditures
May 13, 2022
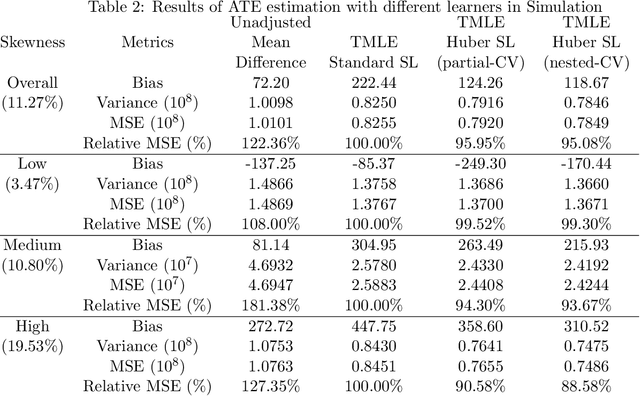
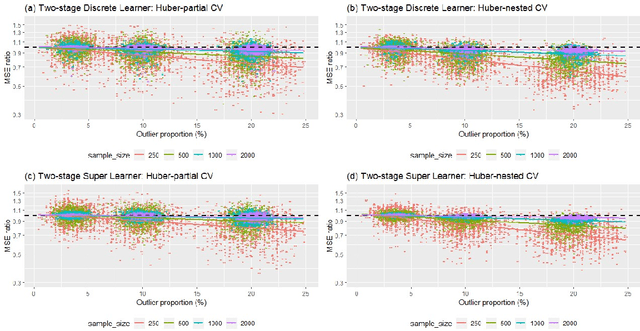
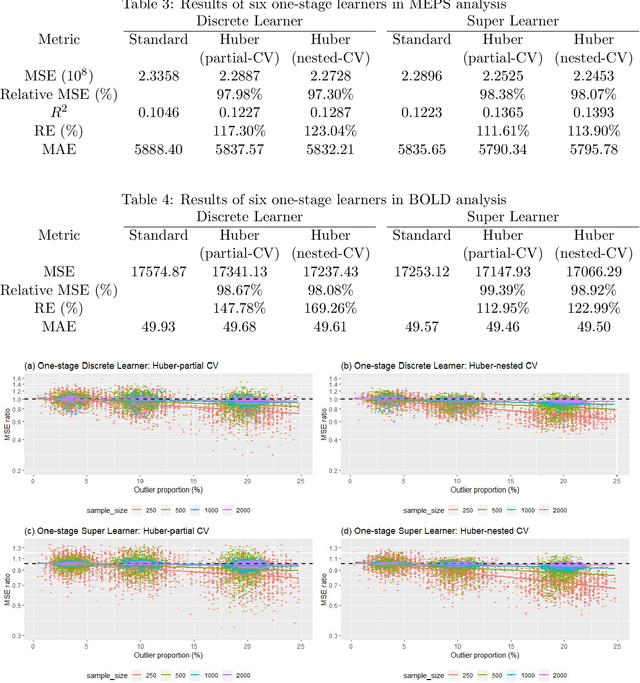
Abstract:Complex distributions of the healthcare expenditure pose challenges to statistical modeling via a single model. Super learning, an ensemble method that combines a range of candidate models, is a promising alternative for cost estimation and has shown benefits over a single model. However, standard approaches to super learning may have poor performance in settings where extreme values are present, such as healthcare expenditure data. We propose a super learner based on the Huber loss, a "robust" loss function that combines squared error loss with absolute loss to down-weight the influence of outliers. We derive oracle inequalities that establish bounds on the finite-sample and asymptotic performance of the method. We show that the proposed method can be used both directly to optimize Huber risk, as well as in finite-sample settings where optimizing mean squared error is the ultimate goal. For this latter scenario, we provide two methods for performing a grid search for values of the robustification parameter indexing the Huber loss. Simulations and real data analysis demonstrate appreciable finite-sample gains in cost prediction and causal effect estimation using our proposed method.
Nonparametric inference for interventional effects with multiple mediators
Jan 16, 2020



Abstract:Understanding the pathways whereby an intervention has an effect on an outcome is a common scientific goal. A rich body of literature provides various decompositions of the total intervention effect into pathway specific effects. Interventional direct and indirect effects provide one such decomposition. Existing estimators of these effects are based on parametric models with confidence interval estimation facilitated via the nonparametric bootstrap. We provide theory that allows for more flexible, possibly machine learning-based, estimation techniques to be considered. In particular, we establish weak convergence results that facilitate the construction of closed-form confidence intervals and hypothesis tests. Finally, we demonstrate multiple robustness properties of the proposed estimators. Simulations show that inference based on large-sample theory has adequate small-sample performance. Our work thus provides a means of leveraging modern statistical learning techniques in estimation of interventional mediation effects.
Flexible Collaborative Estimation of the Average Causal Effect of a Treatment using the Outcome-Highly-Adaptive Lasso
Jun 20, 2018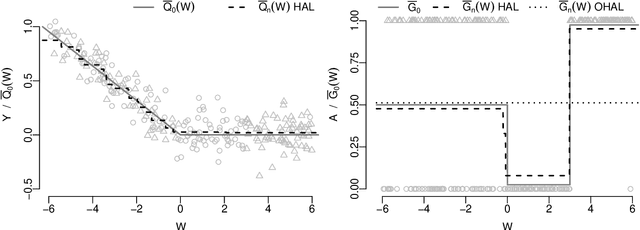
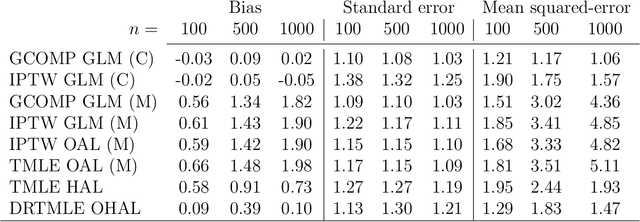
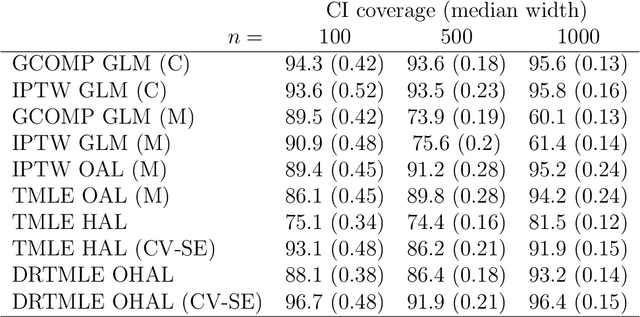
Abstract:Many estimators of the average causal effect of an intervention require estimation of the propensity score, the outcome regression, or both. For these estimators, we must carefully con- sider how to estimate the relevant regressions. It is often beneficial to utilize flexible techniques such as semiparametric regression or machine learning. However, optimal estimation of the regression function does not necessarily lead to optimal estimation of the average causal effect. Therefore, it is important to consider criteria for evaluating regression estimators and selecting hyper-parameters. A recent proposal addressed these issues via the outcome-adaptive lasso, a penalized regression technique for estimating the propensity score. We build on this proposal and offer a method that is simultaneously more flexible and more efficient than the previous pro- posal. We propose the outcome-highly-adaptive LASSO, a semi-parametric regression estimator designed to down-weight regions of the confounder space that do not contribute variation to the outcome regression. We show that tuning this method using collaborative targeted learning leads to superior finite-sample performance relative to competing estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge