Statistical learning for constrained functional parameters in infinite-dimensional models with applications in fair machine learning

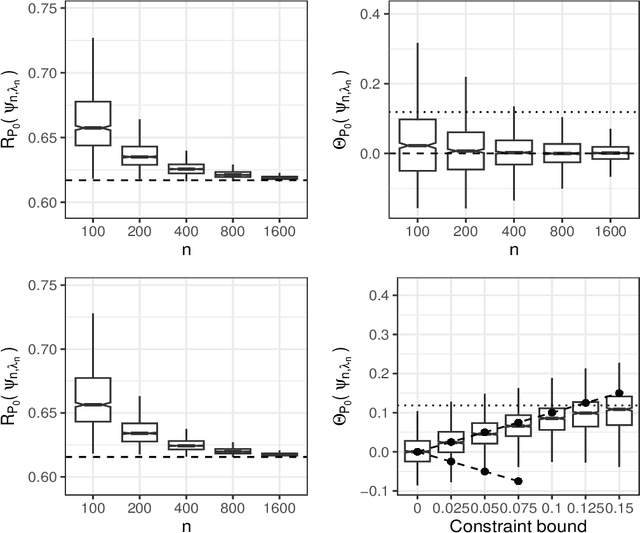
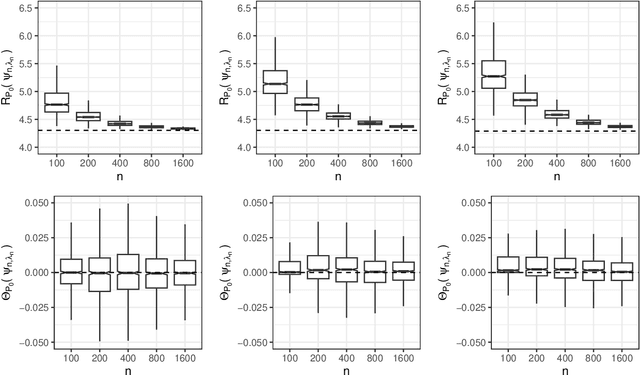
Constrained learning has become increasingly important, especially in the realm of algorithmic fairness and machine learning. In these settings, predictive models are developed specifically to satisfy pre-defined notions of fairness. Here, we study the general problem of constrained statistical machine learning through a statistical functional lens. We consider learning a function-valued parameter of interest under the constraint that one or several pre-specified real-valued functional parameters equal zero or are otherwise bounded. We characterize the constrained functional parameter as the minimizer of a penalized risk criterion using a Lagrange multiplier formulation. We show that closed-form solutions for the optimal constrained parameter are often available, providing insight into mechanisms that drive fairness in predictive models. Our results also suggest natural estimators of the constrained parameter that can be constructed by combining estimates of unconstrained parameters of the data generating distribution. Thus, our estimation procedure for constructing fair machine learning algorithms can be applied in conjunction with any statistical learning approach and off-the-shelf software. We demonstrate the generality of our method by explicitly considering a number of examples of statistical fairness constraints and implementing the approach using several popular learning approaches.

A framework for causal segmentation analysis with machine learning in large-scale digital experiments

We present an end-to-end methodological framework for causal segment discovery that aims to uncover differential impacts of treatments across subgroups of users in large-scale digital experiments. Building on recent developments in causal inference and non/semi-parametric statistics, our approach unifies two objectives: (1) the discovery of user segments that stand to benefit from a candidate treatment based on subgroup-specific treatment effects, and (2) the evaluation of causal impacts of dynamically assigning units to a study's treatment arm based on their predicted segment-specific benefit or harm. Our proposal is model-agnostic, capable of incorporating state-of-the-art machine learning algorithms into the estimation procedure, and is applicable in randomized A/B tests and quasi-experiments. An open source R package implementation, sherlock, is introduced.

Targeting Learning: Robust Statistics for Reproducible Research

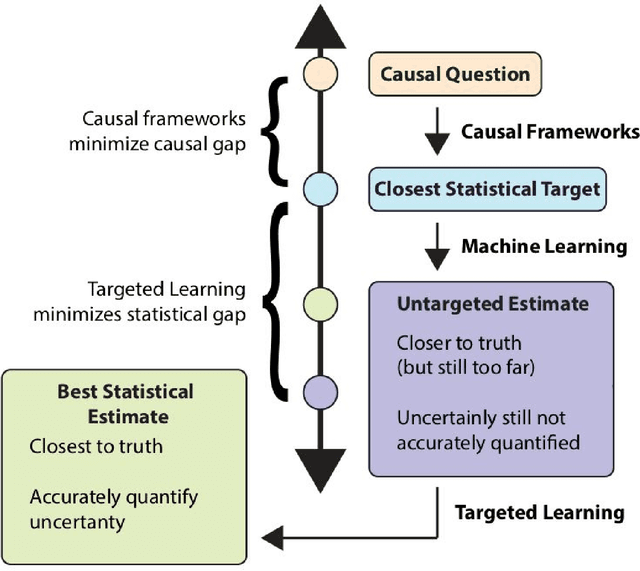
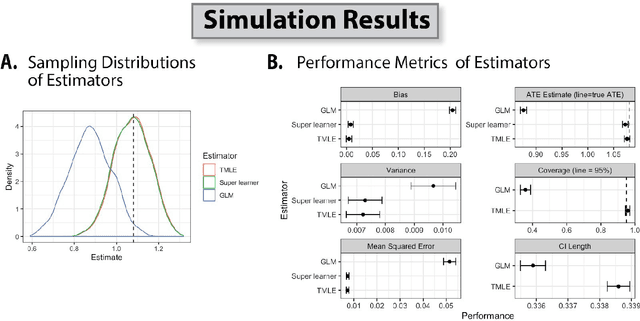
Targeted Learning is a subfield of statistics that unifies advances in causal inference, machine learning and statistical theory to help answer scientifically impactful questions with statistical confidence. Targeted Learning is driven by complex problems in data science and has been implemented in a diversity of real-world scenarios: observational studies with missing treatments and outcomes, personalized interventions, longitudinal settings with time-varying treatment regimes, survival analysis, adaptive randomized trials, mediation analysis, and networks of connected subjects. In contrast to the (mis)application of restrictive modeling strategies that dominate the current practice of statistics, Targeted Learning establishes a principled standard for statistical estimation and inference (i.e., confidence intervals and p-values). This multiply robust approach is accompanied by a guiding roadmap and a burgeoning software ecosystem, both of which provide guidance on the construction of estimators optimized to best answer the motivating question. The roadmap of Targeted Learning emphasizes tailoring statistical procedures so as to minimize their assumptions, carefully grounding them only in the scientific knowledge available. The end result is a framework that honestly reflects the uncertainty in both the background knowledge and the available data in order to draw reliable conclusions from statistical analyses - ultimately enhancing the reproducibility and rigor of scientific findings.

Nonparametric inverse probability weighted estimators based on the highly adaptive lasso

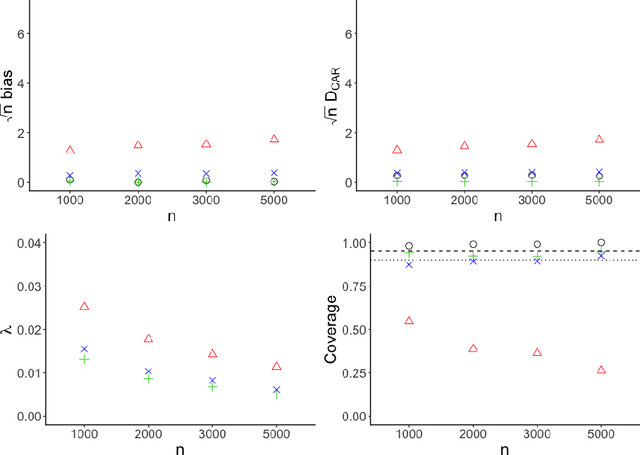
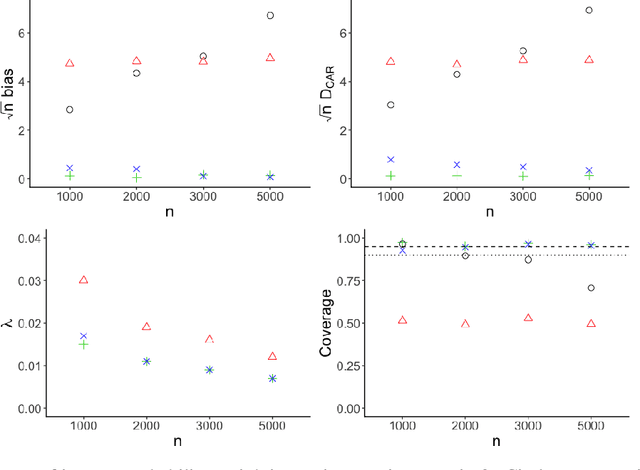
Inverse probability weighted estimators are the oldest and potentially most commonly used class of procedures for the estimation of causal effects. By adjusting for selection biases via a weighting mechanism, these procedures estimate an effect of interest by constructing a pseudo-population in which selection biases are eliminated. Despite their ease of use, these estimators require the correct specification of a model for the weighting mechanism, are known to be inefficient, and suffer from the curse of dimensionality. We propose a class of nonparametric inverse probability weighted estimators in which the weighting mechanism is estimated via undersmoothing of the highly adaptive lasso, a nonparametric regression function proven to converge at $n^{-1/3}$-rate to the true weighting mechanism. We demonstrate that our estimators are asymptotically linear with variance converging to the nonparametric efficiency bound. Unlike doubly robust estimators, our procedures require neither derivation of the efficient influence function nor specification of the conditional outcome model. Our theoretical developments have broad implications for the construction of efficient inverse probability weighted estimators in large statistical models and a variety of problem settings. We assess the practical performance of our estimators in simulation studies and demonstrate use of our proposed methodology with data from a large-scale epidemiologic study.

Data-adaptive statistics for multiple hypothesis testing in high-dimensional settings

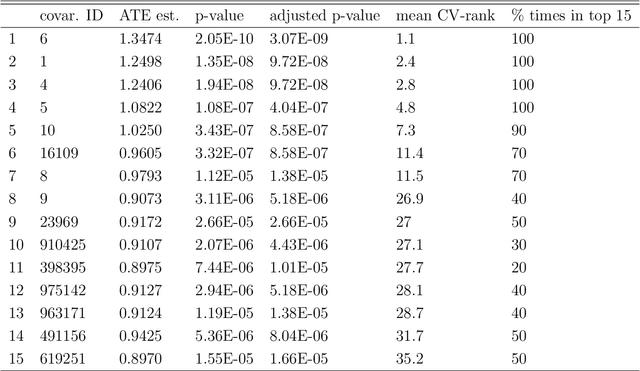
Current statistical inference problems in areas like astronomy, genomics, and marketing routinely involve the simultaneous testing of thousands -- even millions -- of null hypotheses. For high-dimensional multivariate distributions, these hypotheses may concern a wide range of parameters, with complex and unknown dependence structures among variables. In analyzing such hypothesis testing procedures, gains in efficiency and power can be achieved by performing variable reduction on the set of hypotheses prior to testing. We present in this paper an approach using data-adaptive multiple testing that serves exactly this purpose. This approach applies data mining techniques to screen the full set of covariates on equally sized partitions of the whole sample via cross-validation. This generalized screening procedure is used to create average ranks for covariates, which are then used to generate a reduced (sub)set of hypotheses, from which we compute test statistics that are subsequently subjected to standard multiple testing corrections. The principal advantage of this methodology lies in its providing valid statistical inference without the \textit{a priori} specifying which hypotheses will be tested. Here, we present the theoretical details of this approach, confirm its validity via a simulation study, and exemplify its use by applying it to the analysis of data on microRNA differential expression.