Personalised dynamic super learning: an application in predicting hemodiafiltration's convection volumes

Obtaining continuously updated predictions is a major challenge for personalised medicine. Leveraging combinations of parametric regressions and machine learning approaches, the personalised online super learner (POSL) can achieve such dynamic and personalised predictions. We adapt POSL to predict a repeated continuous outcome dynamically and propose a new way to validate such personalised or dynamic prediction models. We illustrate its performance by predicting the convection volume of patients undergoing hemodiafiltration. POSL outperformed its candidate learners with respect to median absolute error, calibration-in-the-large, discrimination, and net benefit. We finally discuss the choices and challenges underlying the use of POSL.

Kernel Debiased Plug-in Estimation

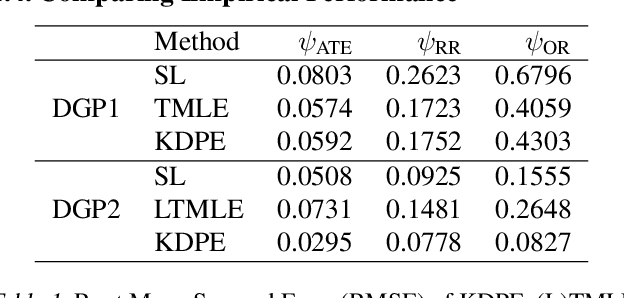
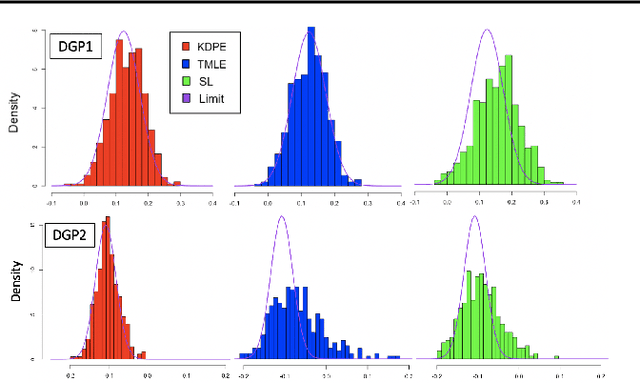
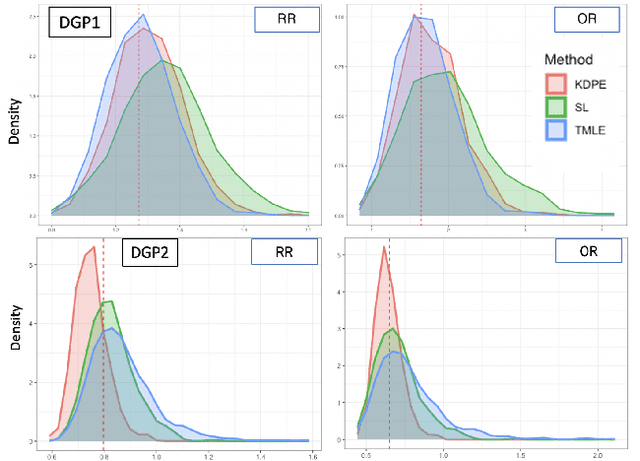
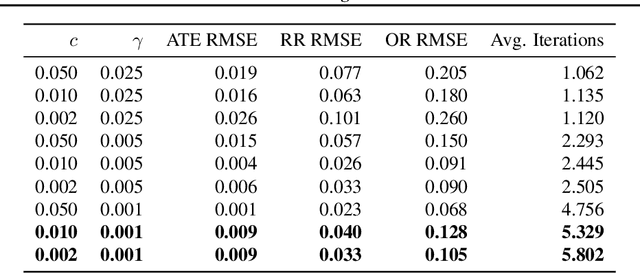
We consider the problem of estimating a scalar target parameter in the presence of nuisance parameters. Replacing the unknown nuisance parameter with a nonparametric estimator, e.g.,a machine learning (ML) model, is convenient but has shown to be inefficient due to large biases. Modern methods, such as the targeted minimum loss-based estimation (TMLE) and double machine learning (DML), achieve optimal performance under flexible assumptions by harnessing ML estimates while mitigating the plug-in bias. To avoid a sub-optimal bias-variance trade-off, these methods perform a debiasing step of the plug-in pre-estimate. Existing debiasing methods require the influence function of the target parameter as input. However, deriving the IF requires specialized expertise and thus obstructs the adaptation of these methods by practitioners. We propose a novel way to debias plug-in estimators which (i) is efficient, (ii) does not require the IF to be implemented, (iii) is computationally tractable, and therefore can be readily adapted to new estimation problems and automated without analytic derivations by the user. We build on the TMLE framework and update a plug-in estimate with a regularized likelihood maximization step over a nonparametric model constructed with a reproducing kernel Hilbert space (RKHS), producing an efficient plug-in estimate for any regular target parameter. Our method, thus, offers the efficiency of competing debiasing techniques without sacrificing the utility of the plug-in approach.

Multi-task Highly Adaptive Lasso

We propose a novel, fully nonparametric approach for the multi-task learning, the Multi-task Highly Adaptive Lasso (MT-HAL). MT-HAL simultaneously learns features, samples and task associations important for the common model, while imposing a shared sparse structure among similar tasks. Given multiple tasks, our approach automatically finds a sparse sharing structure. The proposed MTL algorithm attains a powerful dimension-free convergence rate of $o_p(n^{-1/4})$ or better. We show that MT-HAL outperforms sparsity-based MTL competitors across a wide range of simulation studies, including settings with nonlinear and linear relationships, varying levels of sparsity and task correlations, and different numbers of covariates and sample size.

Adaptive Sequential Surveillance with Network and Temporal Dependence

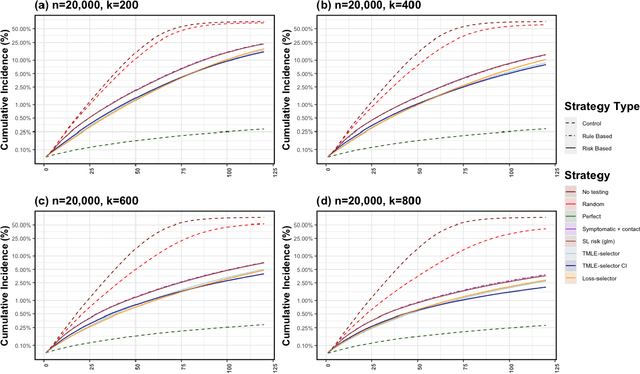
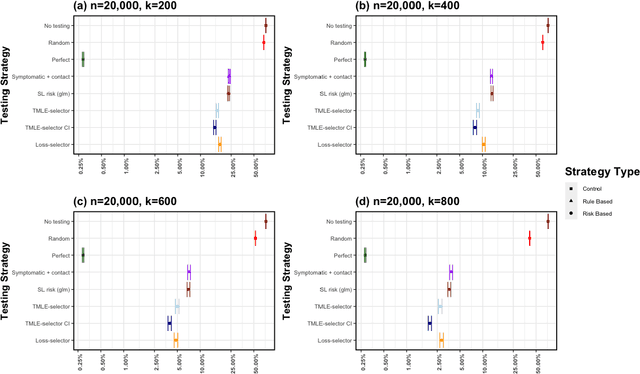
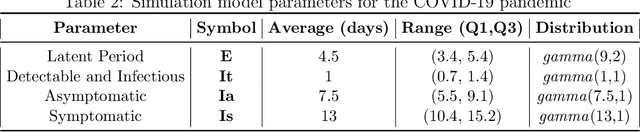
Strategic test allocation plays a major role in the control of both emerging and existing pandemics (e.g., COVID-19, HIV). Widespread testing supports effective epidemic control by (1) reducing transmission via identifying cases, and (2) tracking outbreak dynamics to inform targeted interventions. However, infectious disease surveillance presents unique statistical challenges. For instance, the true outcome of interest - one's positive infectious status, is often a latent variable. In addition, presence of both network and temporal dependence reduces the data to a single observation. As testing entire populations regularly is neither efficient nor feasible, standard approaches to testing recommend simple rule-based testing strategies (e.g., symptom based, contact tracing), without taking into account individual risk. In this work, we study an adaptive sequential design involving n individuals over a period of {\tau} time-steps, which allows for unspecified dependence among individuals and across time. Our causal target parameter is the mean latent outcome we would have obtained after one time-step, if, starting at time t given the observed past, we had carried out a stochastic intervention that maximizes the outcome under a resource constraint. We propose an Online Super Learner for adaptive sequential surveillance that learns the optimal choice of tests strategies over time while adapting to the current state of the outbreak. Relying on a series of working models, the proposed method learns across samples, through time, or both: based on the underlying (unknown) structure in the data. We present an identification result for the latent outcome in terms of the observed data, and demonstrate the superior performance of the proposed strategy in a simulation modeling a residential university environment during the COVID-19 pandemic.

Personalized Online Machine Learning

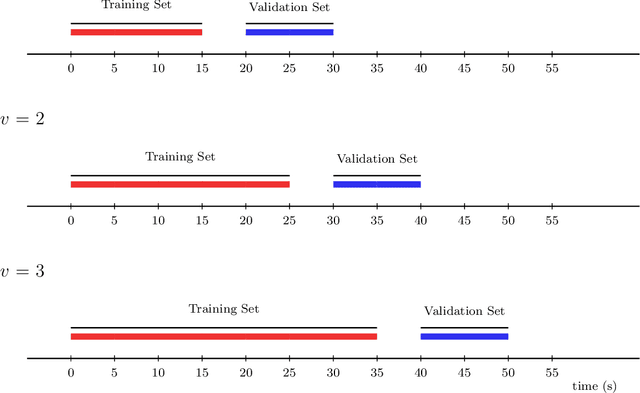
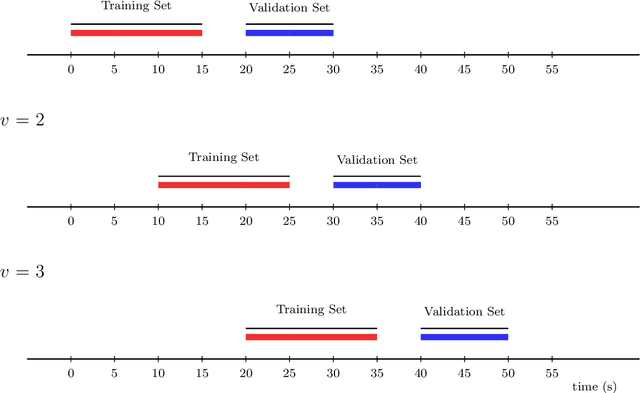
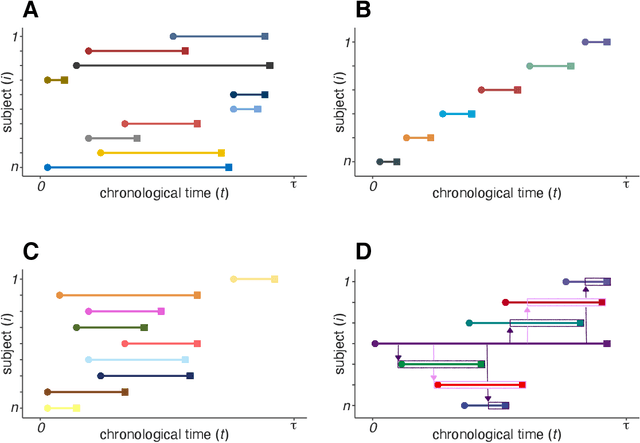
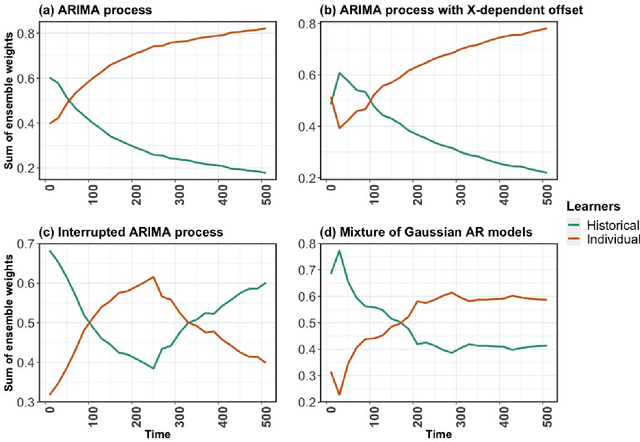
In this work, we introduce the Personalized Online Super Learner (POSL) -- an online ensembling algorithm for streaming data whose optimization procedure accommodates varying degrees of personalization. Namely, POSL optimizes predictions with respect to baseline covariates, so personalization can vary from completely individualized (i.e., optimization with respect to baseline covariate subject ID) to many individuals (i.e., optimization with respect to common baseline covariates). As an online algorithm, POSL learns in real-time. POSL can leverage a diversity of candidate algorithms, including online algorithms with different training and update times, fixed algorithms that are never updated during the procedure, pooled algorithms that learn from many individuals' time-series, and individualized algorithms that learn from within a single time-series. POSL's ensembling of this hybrid of base learning strategies depends on the amount of data collected, the stationarity of the time-series, and the mutual characteristics of a group of time-series. In essence, POSL decides whether to learn across samples, through time, or both, based on the underlying (unknown) structure in the data. For a wide range of simulations that reflect realistic forecasting scenarios, and in a medical data application, we examine the performance of POSL relative to other current ensembling and online learning methods. We show that POSL is able to provide reliable predictions for time-series data and adjust to changing data-generating environments. We further cultivate POSL's practicality by extending it to settings where time-series enter/exit dynamically over chronological time.

Adaptive Sequential Design for a Single Time-Series

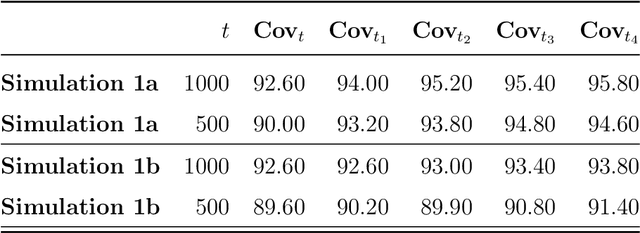
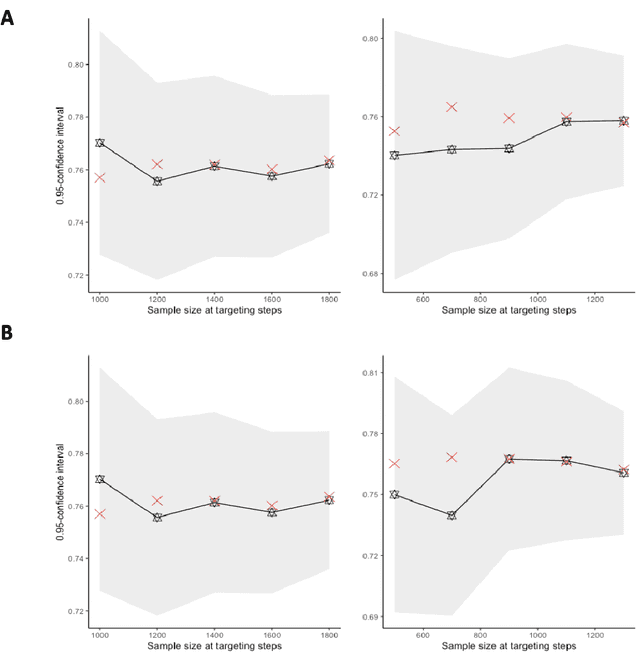
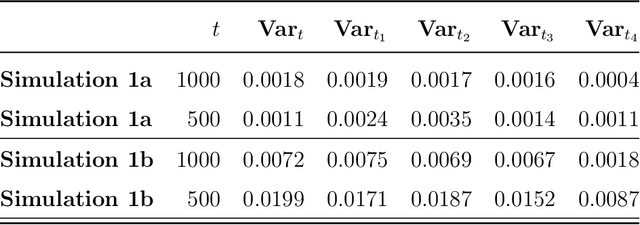
The current work is motivated by the need for robust statistical methods for precision medicine; as such, we address the need for statistical methods that provide actionable inference for a single unit at any point in time. We aim to learn an optimal, unknown choice of the controlled components of the design in order to optimize the expected outcome; with that, we adapt the randomization mechanism for future time-point experiments based on the data collected on the individual over time. Our results demonstrate that one can learn the optimal rule based on a single sample, and thereby adjust the design at any point t with valid inference for the mean target parameter. This work provides several contributions to the field of statistical precision medicine. First, we define a general class of averages of conditional causal parameters defined by the current context for the single unit time-series data. We define a nonparametric model for the probability distribution of the time-series under few assumptions, and aim to fully utilize the sequential randomization in the estimation procedure via the double robust structure of the efficient influence curve of the proposed target parameter. We present multiple exploration-exploitation strategies for assigning treatment, and methods for estimating the optimal rule. Lastly, we present the study of the data-adaptive inference on the mean under the optimal treatment rule, where the target parameter adapts over time in response to the observed context of the individual. Our target parameter is pathwise differentiable with an efficient influence function that is doubly robust - which makes it easier to estimate than previously proposed variations. We characterize the limit distribution of our estimator under a Donsker condition expressed in terms of a notion of bracketing entropy adapted to martingale settings.

Targeting Learning: Robust Statistics for Reproducible Research

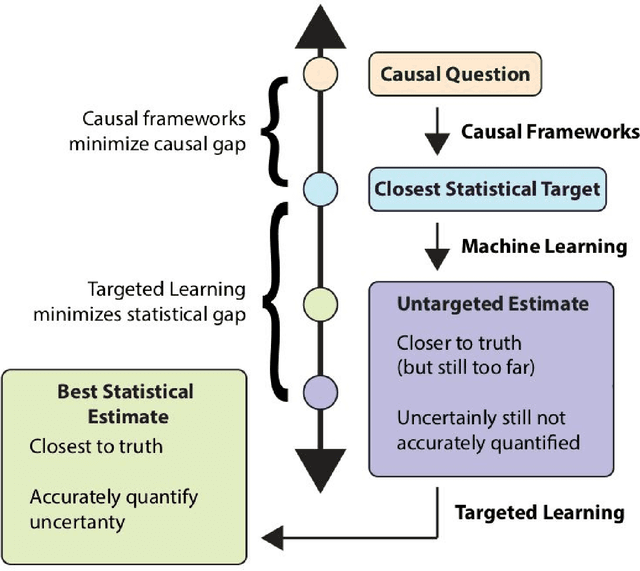
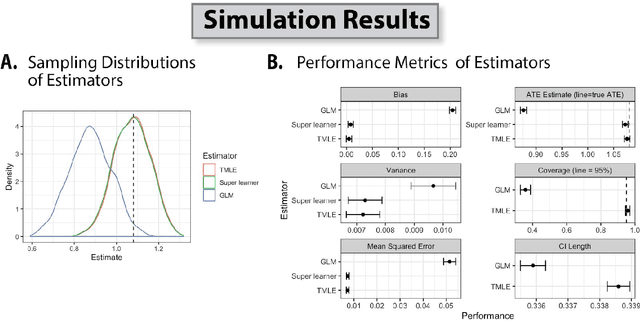
Targeted Learning is a subfield of statistics that unifies advances in causal inference, machine learning and statistical theory to help answer scientifically impactful questions with statistical confidence. Targeted Learning is driven by complex problems in data science and has been implemented in a diversity of real-world scenarios: observational studies with missing treatments and outcomes, personalized interventions, longitudinal settings with time-varying treatment regimes, survival analysis, adaptive randomized trials, mediation analysis, and networks of connected subjects. In contrast to the (mis)application of restrictive modeling strategies that dominate the current practice of statistics, Targeted Learning establishes a principled standard for statistical estimation and inference (i.e., confidence intervals and p-values). This multiply robust approach is accompanied by a guiding roadmap and a burgeoning software ecosystem, both of which provide guidance on the construction of estimators optimized to best answer the motivating question. The roadmap of Targeted Learning emphasizes tailoring statistical procedures so as to minimize their assumptions, carefully grounding them only in the scientific knowledge available. The end result is a framework that honestly reflects the uncertainty in both the background knowledge and the available data in order to draw reliable conclusions from statistical analyses - ultimately enhancing the reproducibility and rigor of scientific findings.

More Efficient Off-Policy Evaluation through Regularized Targeted Learning

We study the problem of off-policy evaluation (OPE) in Reinforcement Learning (RL), where the aim is to estimate the performance of a new policy given historical data that may have been generated by a different policy, or policies. In particular, we introduce a novel doubly-robust estimator for the OPE problem in RL, based on the Targeted Maximum Likelihood Estimation principle from the statistical causal inference literature. We also introduce several variance reduction techniques that lead to impressive performance gains in off-policy evaluation. We show empirically that our estimator uniformly wins over existing off-policy evaluation methods across multiple RL environments and various levels of model misspecification. Finally, we further the existing theoretical analysis of estimators for the RL off-policy estimation problem by showing their $O_P(1/\sqrt{n})$ rate of convergence and characterizing their asymptotic distribution.