Adaptive Sequential Surveillance with Network and Temporal Dependence
Paper and Code
Dec 05, 2022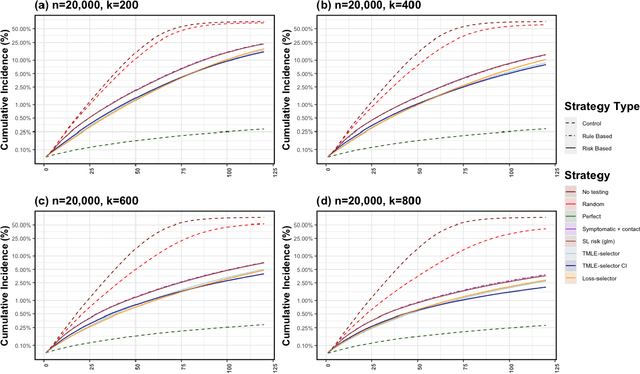

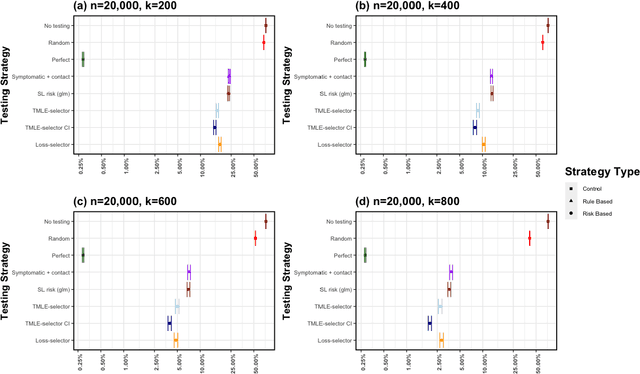
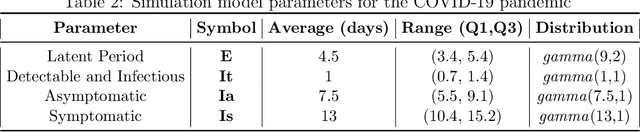
Strategic test allocation plays a major role in the control of both emerging and existing pandemics (e.g., COVID-19, HIV). Widespread testing supports effective epidemic control by (1) reducing transmission via identifying cases, and (2) tracking outbreak dynamics to inform targeted interventions. However, infectious disease surveillance presents unique statistical challenges. For instance, the true outcome of interest - one's positive infectious status, is often a latent variable. In addition, presence of both network and temporal dependence reduces the data to a single observation. As testing entire populations regularly is neither efficient nor feasible, standard approaches to testing recommend simple rule-based testing strategies (e.g., symptom based, contact tracing), without taking into account individual risk. In this work, we study an adaptive sequential design involving n individuals over a period of {\tau} time-steps, which allows for unspecified dependence among individuals and across time. Our causal target parameter is the mean latent outcome we would have obtained after one time-step, if, starting at time t given the observed past, we had carried out a stochastic intervention that maximizes the outcome under a resource constraint. We propose an Online Super Learner for adaptive sequential surveillance that learns the optimal choice of tests strategies over time while adapting to the current state of the outbreak. Relying on a series of working models, the proposed method learns across samples, through time, or both: based on the underlying (unknown) structure in the data. We present an identification result for the latent outcome in terms of the observed data, and demonstrate the superior performance of the proposed strategy in a simulation modeling a residential university environment during the COVID-19 pandemic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge