Machine learning to optimize precision in the analysis of randomized trials: A journey in pre-specified, yet data-adaptive learning

Covariate adjustment is an approach to improve the precision of trial analyses by adjusting for baseline variables that are prognostic of the primary endpoint. Motivated by the SEARCH Universal HIV Test-and-Treat Trial (2013-2017), we tell our story of developing, evaluating, and implementing a machine learning-based approach for covariate adjustment. We provide the rationale for as well as the practical concerns with such an approach for estimating marginal effects. Using schematics, we illustrate our procedure: targeted machine learning estimation (TMLE) with Adaptive Pre-specification. Briefly, sample-splitting is used to data-adaptively select the combination of estimators of the outcome regression (i.e., the conditional expectation of the outcome given the trial arm and covariates) and known propensity score (i.e., the conditional probability of being randomized to the intervention given the covariates) that minimizes the cross-validated variance estimate and, thereby, maximizes empirical efficiency. We discuss our approach for evaluating finite sample performance with parametric and plasmode simulations, pre-specifying the Statistical Analysis Plan, and unblinding in real-time on video conference with our colleagues from around the world. We present the results from applying our approach in the primary, pre-specified analysis of 8 recently published trials (2022-2024). We conclude with practical recommendations and an invitation to implement our approach in the primary analysis of your next trial.

Adaptive Sequential Surveillance with Network and Temporal Dependence

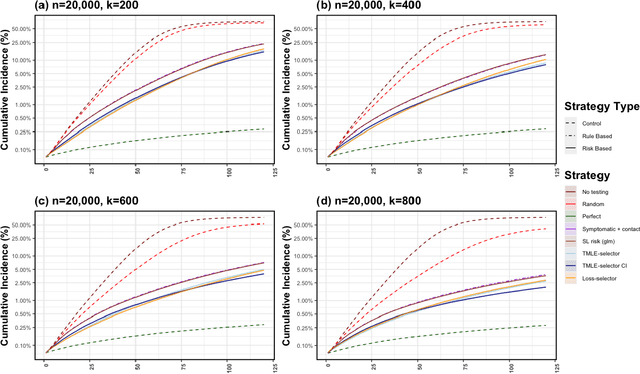
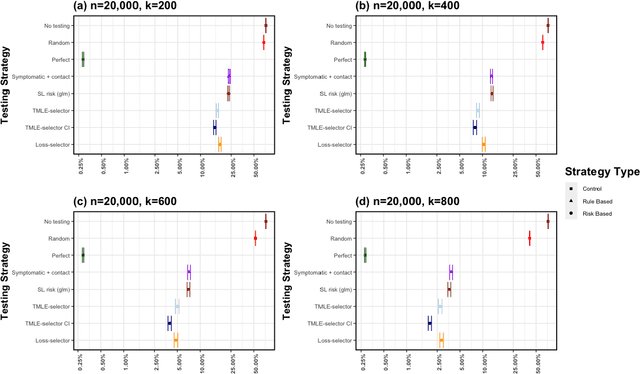
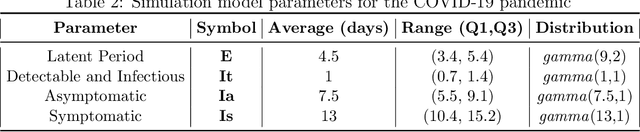
Strategic test allocation plays a major role in the control of both emerging and existing pandemics (e.g., COVID-19, HIV). Widespread testing supports effective epidemic control by (1) reducing transmission via identifying cases, and (2) tracking outbreak dynamics to inform targeted interventions. However, infectious disease surveillance presents unique statistical challenges. For instance, the true outcome of interest - one's positive infectious status, is often a latent variable. In addition, presence of both network and temporal dependence reduces the data to a single observation. As testing entire populations regularly is neither efficient nor feasible, standard approaches to testing recommend simple rule-based testing strategies (e.g., symptom based, contact tracing), without taking into account individual risk. In this work, we study an adaptive sequential design involving n individuals over a period of {\tau} time-steps, which allows for unspecified dependence among individuals and across time. Our causal target parameter is the mean latent outcome we would have obtained after one time-step, if, starting at time t given the observed past, we had carried out a stochastic intervention that maximizes the outcome under a resource constraint. We propose an Online Super Learner for adaptive sequential surveillance that learns the optimal choice of tests strategies over time while adapting to the current state of the outbreak. Relying on a series of working models, the proposed method learns across samples, through time, or both: based on the underlying (unknown) structure in the data. We present an identification result for the latent outcome in terms of the observed data, and demonstrate the superior performance of the proposed strategy in a simulation modeling a residential university environment during the COVID-19 pandemic.

Two-Stage TMLE to Reduce Bias and Improve Efficiency in Cluster Randomized Trials

Cluster randomized trials (CRTs) randomly assign an intervention to groups of individuals (e.g., clinics or communities), and measure outcomes on individuals in those groups. While offering many advantages, this experimental design introduces challenges that are only partially addressed by existing analytic approaches. First, outcomes are often missing for some individuals within clusters. Failing to appropriately adjust for differential outcome measurement can result in biased estimates and inference. Second, CRTs often randomize limited numbers of clusters, resulting in chance imbalances on baseline outcome predictors between arms. Failing to adaptively adjust for these imbalances and other predictive covariates can result in efficiency losses. To address these methodological gaps, we propose and evaluate a novel two-stage targeted minimum loss-based estimator (TMLE) to adjust for baseline covariates in a manner that optimizes precision, after controlling for baseline and post-baseline causes of missing outcomes. Finite sample simulations illustrate that our approach can nearly eliminate bias due to differential outcome measurement, while other common CRT estimators yield misleading results and inferences. Application to real data from the SEARCH community randomized trial demonstrates the gains in efficiency afforded through adaptive adjustment for cluster-level covariates, after controlling for missingness on individual-level outcomes.